3. Задание.
Задание
2. Приборный
блок установлен на упругие опоры
(амортизаторы). Его вертикальные колебания
описываются дифференциальным уравнением:
,
где
- отклонение блока от исходного положения,
- время,
– масса блока,
- ускорение,
– коэффициент трения (в амортизаторах),
- скорость движения при колебаниях
блока,
- слагаемое, отвечающее за сопротивление
упругих элементов (пружин),
- коэффициент жесткости амортизаторов.
Амортизаторы имеют
встроенные демпфирующие элементы.
Поэтому коэффициент трения
зависит от деформации
.
Решите уравнение
для следующих исходных данных: коэффициент
трения
Н/м; начальные условия
см и
при
.
Остальные параметры заданы в таблице.
Таблица 1. Таблица начальных данных для всех вариантов задания 2.
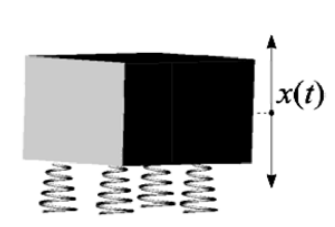Рис.
6. Блок на
амортизаторах.
Получите начальные
точки решения, охватывающие несколько
периодов колебаний, и постройте по ним
соответствующий участок зависимости
.
4. Решение задания в MathCad.
В системах MathCAD имеются удобные в практическом применении средства для решения линейных и нелинейных дифференциальных уравнений и систем этих уравнений. Для этого предусмотрен ряд встроенных функций (rkfixed, odesolve).
Решение уравнения методом Рунге-Кутта с помощью оператора Odesolve. Встроенная функция odesolve(x, x2,[m]) обеспечивает решение одного обыкновенного дифференциального уравнения методом Рунге-Кутта с постоянным (по умолчанию) или адаптивно вычисляемым системой шагом интегрирования. Формат функции odesolve предполагает указание в числе ее аргументов переменной интегрирования, ее правого граничного значения и числа точек, в которых будет найдено решение, то есть odesolve(x, x2,[m]), где квадратные скобки означают, что указание числа точек, в которых ищется решение, не обязательно. Результатом применения odesolve служит функция у(х), аргумент которой определен на интервале (xl, х2). Эта функция может быть непосредственно использована для построения графика и вывода ее числового значения при фиксированном значении аргумента.
Решение
уравнения методом Рунге-Кутта с помощью
оператора rkfixed.
Встроенная
функция rkfixed
(y0,t0,tk,N,f)
обеспечивает решение уравнений методом
Рунге-Кутта с постоянным шагом
интегрирования, равным (tk
– t0)/N.
При ее использовании следует учесть,
что предварительно в документе MathCAD
должны быть введены: векторная функция
f(t,y)
с указанием ее аргументов и начальный
вектор состояний. Результаты решения
задач интегрирования систем дифференциальных
с помощью rkfixed
формируются системами MathCAD
в виде (l+
1)
* (п
+ 1)
- матрицы (таблицы), первый столбец
которой содержит значения аргументов
от t0
до tk,
а остальные п
ее
столбцов образуются значениями элементов
вектора у
переменных состояний исследуемой
системы. Таким образом, число элементов
каждого 
из
столбцов результирующей матрицы
определяется параметром l,
введенным
в качестве аргумента соответствующей
функции.
4.1. Метод Эйлера.
Рис. 7. Вычисления по методу Эйлера.
Рис. 8. Решение по методу Эйлера.
Рис. 9. График зависимости x(t).
Колебания, протекающие по закону косинуса:
,
где
– начальная амплитуда (она же является
максимальной),
- коэффициент затухания,
- начальная фаза колебаний,
– циклическая частота колебаний (число
колебаний за
секунд),
- механическая частота колебаний (число
колебаний в единицу времени – в секунду),
- период колебаний (время, за которое
совершено одно полное колебание (на
графике – расстояние между двумя
соседними максимумами функции). По
графику можно вычислить:
м,
с,
Гц,
Гц.
Необходимо заметить, что колебания блока на амортизаторах имеют периодический характер, затухают и со временем прекращаются, что мы наглядно видим на рис. 9.
Рис. 10. Уменьшение шага метода Эйлера.
Рис. 11. Решение по методу Эйлера с уменьшенным в 2 раза шагом.
Рис. 12. График зависимости x(t) с уменьшенным вдвое шагом.
Колебания, протекающие по закону косинуса:
, где – начальная амплитуда (она же является максимальной), - коэффициент затухания, - начальная фаза колебаний, – циклическая частота колебаний (число колебаний за секунд), - механическая частота колебаний (число колебаний в единицу времени – в секунду), - период колебаний (время, за которое совершено одно полное колебание (на графике – расстояние между двумя соседними максимумами функции). По графику можно вычислить:
м,
с,
Гц,
Гц.
Исходя из рис. 12, характер графика, показанный на рис. 9, не претерпел изменений, что доказывает правильность выбора нового шага.
Рис. 13. Погрешность метода Эйлера.