Розділ 4 електричні властивості твердих тіл

4.1 Приклади рішення задач

4.1.1 Електропровідність металів

1. По залізному провіднику ⁵⁶Fe діаметром 0,6мм тече струм силою 16 А. Визначити середню швидкість спрямованого руху електронів, вважаючи, що кількість вільних електронів в одиниці об’єму дорівнює кількості атомів. Густина заліза 7,8·10³кг/м³.

Д ано: Рішення

M = 56∙10^-3 кг/моль

d = 0,6 мм = 6∙10^-4 м

I = 16 А

ρ = 7,8∙10³ кг/м³

‹υ› - ?

Середня швидкість руху електронів в провіднику дорівнює:

, (1)

де t – час, за який електрон проходе ділянку провідника довжиною l. При цьому електрони переносять заряд q = Nе і створюють струм силою:

, (2)

де N – кількість електронів на ділянці провідника l. Знайдемо концентрацію електронів в провіднику

, (3)

але з другого боку

, (4)

де . Зрівняємо формули (3) та (4):

Отримаємо:

(5)

Підставимо формулу (5) у (2): і знайдемо l :

(6)

Враховуючи формулу (6) в (1) та те, що , отримаємо:

2. По мідному дроту тече струм густиною 1 А/мм². Враховуючи, що на кожний атом міді припадає один вільний електрон, оцінити, який шлях пройде електрон, перемістившись уздовж дроту на відстань 10 мм при кімнатній температурі. Густина міді 8,9·10³кг/м³.

Д ано: Рішення

M = 63∙10^-3 кг/моль

j = 1 А/мм² = 1·10⁶А/м²

l = 10мм = 1·10^-2м

Т = 300К

ρ = 8,9·10³кг/м³

S - ?

Враховуємо, що рухаючись по провіднику з дрейфовою швидкістю , електрон бере також участь у хаотичному тепловому русі з середньою швидкістю υ. Тоді шлях, який пройде електрон за час t, рухаючись рівномірно, буде дорівнювати:

(1)

З формули для густини струму знайдемо час проходження електрона уздовж провідника: ,

звідси

, (2)

де - дрейфова швидкість електрона. Підставляючи формулу (2) в (1), отримаємо:

Враховуємо, що - концентрація електронів провідності в міді, а , m – маса електрона. Тоді

м

3. У мідному провіднику довжиною 2 м і площею поперечного перерізу 0,4 мм² тече струм. При цьому за 1с виділяється 0,35 Дж теплоти. Скільки електронів проходе крізь поперечний переріз цього провідника? Питомий електроопір міді прийняти рівним 0,17·10^-7Ом·м.

Д ано: Рішення

l = 2м

S = 0,4 мм² = 4·10^-7м²

t = 1с

Q = 0,35Дж

ρ = 0,17·10^-7Ом·м

N - ?

Кількість електронів N, які проходять крізь переріз провідника за час t, знайдемо з формули, яка визначає фізичний зміст сили електричного струму:

,

де - заряд, який проходе крізь переріз провідника за час t. Звідси

(1)

Силу струму можна знайти з закону Джоуля-Ленца: , тоді

, (2)

а електроопір провідника за формулою:

(3)

Тоді, підставляючи формулу (2) в (1) та враховуючи формулу (3), маємо:

4. Питома електропровідність натрію при 300 К дорівнює 2,17·10⁷ Ом^-1·м^-1, а відношення маси електрона до його ефективної маси дорівнює 1,2. Густина натрію 0,97 г/см³. Обчислити: а) час релаксації і середню довжину вільного пробігу електронів при 300К; б) дрейфову швидкість та рухомість носіїв в електричному полі напруженістю 100 В/м.

Д ано: Рішення

М = 23·10^-3кг/моль а) Відповідно до квантової теорії електропро-

Т = 300К відності

σ = 2,17·10⁷ Ом^-1·м^-1 (1)

Враховуючи, що на один атом Nа припадає один

ρ = 0,97г/см³ = 970 кг/м³ вільний електрон, знайдемо концентрацію електро-

Е ₀ = 100 В/м нів в кристалі:

τ-? -? u=? μ-? (2)

Тоді з формули (1), враховуючи формулу (2), знайдемо час релаксації:

с,

де - m/1,2.

Приймаємо до уваги, що середня швидкість теплового руху електронів υ значно більша дрейфової швидкості u (υ >> u), тоді середня довжина вільного пробігу електронів буде дорівнювати:

(3)

Враховуючи, що середня кінетична енергія поступального руху електронів дорівнює:

або ,

можна знайти υ:

, тобто (4)

Тоді, підставляючи формулу (4) в (3), отримаємо:

м

б ) Знайдемо дрейфову швидкість з рівняння стаціонарного руху електрона, коли кулонівська сила скомпенсована силою опору :

, (5)

де

, (6)

В скалярному вигляді рівняння (5) запишеться:

,

тобто F = F₀ або враховуючи формули (6), отримаємо:

Звідки

За визначенням фізичного змісту, рухомість дорівнює:

4.1.2 Електропровідність напівпровідників

1 . Визначити ширину забороненої зони власного напівпровідника, якщо при температурах Т₁ та Т₂ (Т₂ > Т₁) його електроопори відповідно дорівнюють R₁ та R₂.

Дано: Рішення

Т ₁

Т₂

Т₂ > Т₁

R₁

R ₂

ΔЕ - ?

Залежність питомого електроопору напівпровідника від температури визначається виразом

,

Врахуємо, що ρ ~ R, тоді можна записати:

.

Запишемо відношення електроопорів при температурах Т₁ і Т₂:

.

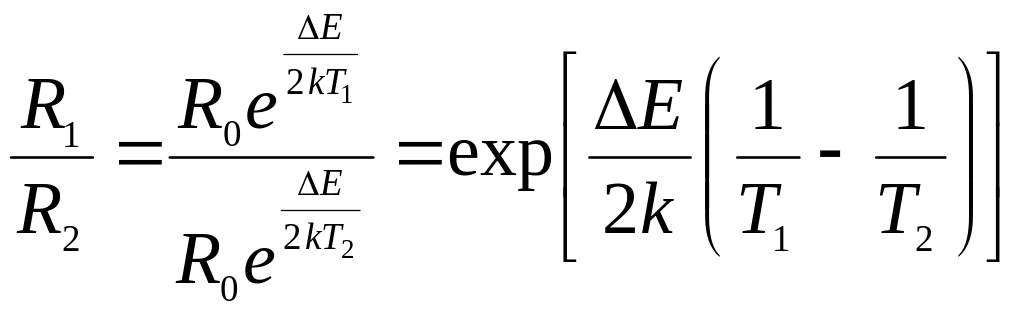Прологарифмуємо отримане рівняння і знайдемо ширину забороненої зони:

,

звідси:

2 . Знайти мінімальну енергію, яка необхідна для створення пари електрон-дірка в кристалі , якщо його електропровідність змінюється в 10 разів при зміненні температури від +20⁰С до -3⁰С.

Д ано: Рішення

Т₁ = 20⁰С + 273 = 293К

Т ₂ = -3⁰С + 273 = 270К

Е - ?

Температурна залежність питомої електропровідності напівпровідників визначається виразом:

Знайдемо відношення питомих електропровідностей при температурах Т₁ і Т₂:

Прологарифмуємо отриманий вираз і перетворимо його для отримання енергетичної ширини забороненої зони ΔЕ, оскільки ΔЕ і є енергією, необхідною для створення пари електрона і дірки:

Тоді

Дж = 1,37еВ

3. В кристалі кремнію масою 120 г, рівномірно по об’єму розподілені 25,7 мкг фосфору та 38,2 мкг галію . Враховуючи, що атоми домішок повністю іонізовані, розрахувати питомий опір кристалу. Густину кремнію прийняти 2,35 г/см³, а рухливість електронів та дірок відповідно 0,38 та 0,18 м²/В·с.

Д ано: Рішення

= 120 г = 0,12 кг Враховуємо, що Р – елемент V групи, тобто донор,

= 25,7 мкг = 25,7·10^-9 кг і має електронну провідність, а - ІІІ групи, тобто

= 31·10^-3 кг/моль акцептор, і має діркову провідність. При цьому

= 38,2 мкг = 38,2·10^-9 кг відомо, що питома електропровідність домішкового

=69·10^-3 кг/моль напівпровідника , тоді

d = 2,35 г/см³ = 2,35·10³ кг/м³ (1)

= 0,38м²/В·с Концентрації електронів n і дірок р знайдемо за

= 0,18м²/В·с формулами:

ρ - ? ; ,

де - об’єм кремнію, а , - число атомів Р і Ga, яке дорівнює, відповідно, числу електронів n і дірок р. Тоді

, (2)

Підставляючи формулу (2) в (1), отримаємо:

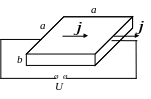
4. Зразок германію, що має форму прямокутного паралелепіпеда розмірами 02 х 0,2 х 0,05 см³ містить концентрацію вільних зарядів 10²¹ м^-3. До двох протилежних вузьких граней прикладена напруга 20 В. Обчислити величину струму, вважаючи, що рухомість носіїв заряду дорівнює 0,03 м²/В^.с.

Д ано: а = 0,2 см = 20∙10-4 м b = 0,05 см = 5∙10-4 м n = 1021 м-3 U = 20 B μ = 0,03 м2/В.с І - ?

Рішення

Сила струму дорівнює:

, (1)

де площа поперечного перерізу зразка .

Густина струму за законом Ома

,

де - питома електропровідність, тобто

,

але напруженість електричного поля

,

тоді

(2)

Враховуючи формулу (2) в (1), отримаємо:

А

4.1.3 Ефект Холла

1. Стала Холла для алюмінію дорівнює приблизно – 0,36·10^-10м³/Кл. Скільки електронів, в середньому на один атом, приймає участь у процесі провідності? Густина алюмінію 2,6 г/см³.

Д ано: Рішення

М = 27·10^-3кг/моль Кількість електронів провідності, що припа-

R = -0,36·10^-10м³/Кл дають на один атом алюмінію, знайдемо як

ρ = 2,6г/см³ = 2,6·10³кг/м³ відношення концентрації вільних електронів в

N-? кристалі n_е до концентрації атомів n_а:

(1)

З формули для сталої Холла: , знайдемо концентрацію електронів провідності

(2)

А концентрацію атомів за формулою

, (3)

де - об’єм одного моля алюмінію. Тоді підставляючи формули (2) і (3) в (1), отримаємо:

2. Платівка напівпровідника завширшки 1см і довжиною 2см розміщена в однорідному магнітному полі з індукцією 0,2 Тл. Вектор магнітної індукції перпендикулярен широкій площині платівки. До кінців платівки прикладено напругу 60 В. Визначити холлівську напругу, якщо стала Холла дорівнює 0,1м³/Кл, а питомий електроопір платівки 0,5 Ом·м.

Д ано: Рішення

b = 1см = 1·10^-2 м

l = 2 см = 2·10^-2 м

В = 0,2 Тл

U = 60 В

R = 0,1 м³/Кл

ρ = 0,5 Ом·м

U_х - ?

Напругу Холла знаходимо за формулою:

(1)

З закону Ома , враховуючи, що напруженість електричного поля , знайдемо густину електричного струму

(2)

Підставляємо формулу (2) в (1), отримаємо:

В

3. Зразок германію n-типу у вигляді платівки довжиною 10 мм та шириною 6 мм розміщено перпендикулярно лініям індукції однорідного магнітного поля 0,1 Тл. При напрузі 25 В, яка прикладена до кінців платівки, виникає холлівська різниця потенціалів 8,8 мВ. Визначити сталу Холла та концентрацію носіїв струму. Питому електропровідність германію прийняти рівною 80 Ом^-1м^-1.

Д ано: Рішення

l = 10мм = 1·10^-2м

b= 6мм = 6·10^-3м

В = 0,1Тл

U = 25 В

U_х = 8,8 мВ = 8,8·10^-3 В

σ = 80 Ом^-1м^-1

R-? n-?

З формули для холлівської різниці потенціалів визначимо сталу Холла

(1)

За законом Ома густина струму дорівнює:

, (2)

де - напруженість електричного поля, яка створює електричний струм в платівці.

Підставляючи формулу (2) в (1), отримаємо:

Концентрацію носіїв струму у зразку германію знаходимо з формули для сталої Холла

,

звідси: м^-3

4.2 Задачі для самостійного розв’язання

1. Сила струму у металевому провіднику 0,8 А, переріз провідника 4 мм², концентрація вільних електронів 2,5∙10²² см^-3.Визначити середню швидкість їх упорядкованого руху. (‹υ› = 5∙10^-5 м/с)

2. Густина струму в алюмінієвому провіднику 1 А/мм². Знайти середню швидкість упорядкованого руху електронів, припускаючи, що кількість вільних електронів в 1 см³ алюмінію дорівнює числу атомів . ( ‹υ› = 1∙10^-4 м/c)

3. Обчислити рухомість електронів у натрію при 0⁰С, якщо його електропровідність при цій температурі 0,23·10⁸Ом^-1·м^-1. Прийняти, що на кожний атом натрію припадає по одному вільному електрону. Густина натрію 970 кг/м³ (μ = 7·10^-2м²/В·с)

4. Електропровідність міді 6∙10⁷ Ом^-1м^-1. Визначити час релаксації електронів, враховуючи, що кожний атом міді у твердому стані віддає у зону провідності один валентний електрон. (τ = 2,5∙10^-14 с)

5. Обчислити швидкість дрейфу електронів у міді при накладенні електричного поля напруженістю 100 В/м. Підрахувати відношення швидкості Фермі до швидкості дрейфу, якщо енергія Фермі для міді дорівнює 7 еВ, густина міді 8,89 г/см³, а питомий електроопір 1,7·10^-8Ом·м. (u = 0,44 м/с; = 3,6∙10^-6)

6. Питомий електроопір срібного дроту при кімнатній температурі 1,54·10^-8Ом·м. Обчислити середню швидкість дрейфу електронів при напруженості електричного поля уздовж провідника 1В/см, вважаючи, що в 1см³ знаходиться 5,8·10²⁸ електронів провідності. Визначити рухомість і час релаксації електронів. (u = 0,69м/с; μ = 6,9·10^-3м²/В·с, τ = 4·10^-14с)

7. Ширина забороненої зони у чистому германії складає 0,72 еВ. У скільки разів розрізняються концентрація електронів провідності при 20⁰С і при 40⁰С? (n₂/n₁ = 2,5)

8. Кремній , який леговано 1·10^-6ат.% алюмінію має при 20⁰С питомий електроопір 0,25 Ом·м. Визначити концентрацію дірок, вважаючи, що акцепторна домішка повністю іонізована. Знайти рухомість дірок. Густина кремнію 2,35г/см³. (n = 5,1·10²⁰м^-3, μ = 4,9·10^-2м²/В·с)

9. Питомий електроопір германію при 27 ⁰С дорівнює 0,47 Ом∙м. Припускаючи, що рухомість електронів і дірок відповідно дорівнюють 0,38 і 0,18 м²/В∙с, обчислити концентрацію носіїв струму. (n = 2,4∙10¹⁹ м^-3)

10. Обчислити електропровідність германію, який містить індій у концентрації 2∙10²² м^-3 і сурму у концентрації 1∙10²¹ м^-3. Врахувати, що індій є акцептором, а сурма – донором, а рухомість електронів і дірок відповідно дорівнюють 0,38 і 0,18 м²/В∙с ( σ = 637 Ом^-1м^-1)

11. Обрахувати температурний коефіцієнт електроопору германію при температурі 300К, якщо ширина забороненої зони дорівнює 0,7 еВ. (α = 4,5·10^-2К^-1)

12. Обчислити сталу Холла для міді ⁶⁴Cu. Густина міді 8,86∙10³ кг/м³. (R = 7,4∙10^-11 м³/Кл)

13. Тонка платівка з кремнію, завширшки 2 см, розміщена перпендикулярно лініям однорідного магнітного поля з індукцією 0,5 Тл. При густині струму 2 мкА/мм², спрямованого уздовж платівки, холівська напруга дорівнює 2,8 В. Визначити концентрацію носіїв струму. (n = 4,5·10¹⁶м^-3)

14. Питома провідність кремнію з домішками дорівнює 112 Ом^-1м^-1. Визначити рухомість дірок і їх концентрацію, якщо стала Холла дорівнює 3,66∙10^-4 м³/Кл. Прийняти, що напівпровідник має тільки діркову провідність. (μ_р = 4,1∙10^-2 м²/В∙с; р = 1,7∙10²² м^-3)

15. У зразку германію рухомість електронів 0,38 м²/В·с, а дірок 0,16м²/В·с. У цьому зразку ефект Холла не спостерігається. Яка частина струму переноситься дірками? ( )