Розділ 3 теплові властивості твердих тіл

3.1 Приклади рішення задач

1. Обчислити молярну електронну теплоємність міді ⁶⁴Сu при 2 К і 1000 К та співставити її з теплоємністю решітки при тих самих температурах. Температура Дебая для міді 316 К, густина 8,93∙10³кг/м³.

Дано: Рішення

М = 64∙10^-3 кг/моль Електронна теплоємність металу визначається

Т₁ = 2 К за формулою:

Т₂ = 1000 К ( 1)

θ = 316 К

ρ = 8,93∙10³ кг/м³ Врахуємо, що енергія Фермі

C_e1 - ? C_p1-? , (2)

C _e2 - ? C_p2 - ?

де n – концентрація електронів провідності, m – їх ефективна маса. Знайдемо концентрацію вільних електронів в міді, вважаючи, що кожний атом віддає по одному електрону:

(3)

Підставимо формулу (2) в (1), враховуючи (3), і отримаємо:

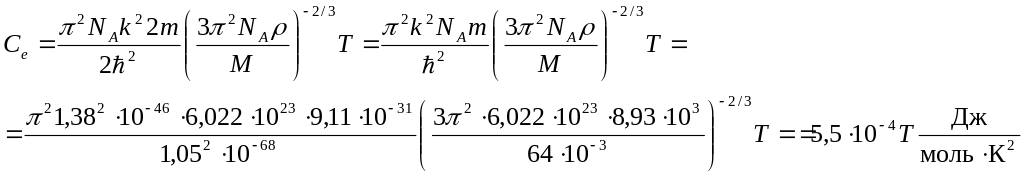
Тому:

С_е1=5,4∙10^-4∙2= 1,08∙10^-3 ;

С_е2=5,4∙10^-4∙10³= 0,54 ;

Решіточна теплоємність при низьких температурах, Т<<θ, знаходиться за теорією Дебая:

При Т > θ з хорошим наближенням можна користуватися законом Дюлонга і Пті:

C_p2 = 3R = 3∙8,31 = 24,9

Таким чином, при високих температурах (Т > θ) решіточна складова теплоємності значно перевищує електронну, а при низьких (Т << θ) – електронна теплоємність може перебільшувати решіточну складову.

2. Знайти кількість теплоти, яка необхідна для нагрівання кристала молібдену ⁹⁶Мо масою 50 г від 15 до 25 К. Температура Дебая молібдену 425 К.

Дано: Рішення

М = 96∙10^-3 кг/моль З формули, що визначає фізичний зміст молярної

m = 50 г = 5∙10^-2 кг теплоємності , знайдемо

Т₁ = 15 К кількість теплоти:

Т₂ = 25 К

θ = 425 К (1)

Q - ?

За теорією Дебая для Т << θ:

(2)

Тоді підставляючи формулу (2) в (1) і виконуючи інтегрування, отримаємо:

3. Молярна теплоємність молібдену при 20 К дорівнює 0,5 Дж/(моль∙К). Обчислити температуру Дебая. Умови Т << θ вважати виконаними.

Дано: Рішення

Т = 20 К При Т << θ, молярну теплоємність можна знайти

С = 0,5 Дж/моль∙К з теорії Дебая:

θ - ?

Звідси температура Дебая:

4. Обчислити питому теплоємність германію при 20К. Температура Дебая для дорівнює 370К.

Д ано: Рішення

М = 73·10^-3кг/моль З формул, які визначають фізичний зміст питомої:

Т = 20К та молярної

θ = 370К теплоємкостей, запишемо:

с - ?

, (1)

де - кількість речовини. Відповідно до теорії Дебая, при Т << θ, молярну теплоємність знайдемо за формулою:

(2)

Підставляючи формулу (2) в (1), отримаємо:

3.2 Задачі для самостійного розв’язання

1.Обчислити теплоємність одиниці об’єму кристала броміду алюмінію (AlBr₃) при температурі, яка вища температури Дебая. Густина кристалу 3,01∙10³ кг/м³, молекулярна маса 267. (С = 0,28 МДж/м³ К)

2. Обчислити питому теплоємність кристалів алюмінію і міді при температурі більшої температури Дебая. (с₁ =923 Дж/кг К, с₂ = 389 Дж/кг·К)

3. Визначити кількість теплоти, яка необхідна для нагрівання кристала NaCl массою 20 г на 2 К. Розглянути два випадки: 1) нагрівання відбувається від температури Дебая; 2) нагрівання відбувається від Т = 2 К. Температура Дебая для NaCl дорівнює 320 К. Молекулярна маса NaCl 58,5. (Q₁ = 16,3Дж, Q₂ = 1,22∙10^-3 Дж)

4. Знайти кількість теплоти, необхідної для нагрівання кристала міді масою 50 г від 15 К до 25 К. Температура Дебая для міді дорівнює 339К. (Q = 3,31Дж)

5. Теплоємність срібла при 10 К дорівнює 0,199 Дж/моль∙К. Визначити температуру Дебая. (θ = 214 К)