Задание 6

Определить дебит галереи, падение давления (по сравнению с контурным) в сечение L, от контура питания, и соотношение времени прохождения частиц нефти в каждом из пропластков от этого сечения до галереи при следующих исходных данных.

Дано: СИ: Решение:

– 4,2 м 1) Дебит галереи:

– 7 м

– 8 м 2) Распределение давления определяется:

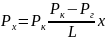– 0,8 Д * где x =

– 0,4 Д * 3) Падение давление от контура питания

– 0,5 Д * до сечения :

– 0,2 %

– 0,16 % 4) Отношение времени движения частиц

– 0,19 % жидкости в разных пропластках

Δp – 30 * определяется из равенства:

ρ – 800

μ – 3,7 с*П * где l=B

L – 5 км *1000 м

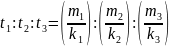
B – 220 м

– 1800 м

Вычисление:

2)

3)

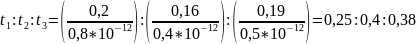
Ответ: Q = ; = ; ) =

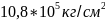Движение границы раздела двух жидкостей с учетом неполноты вытеснения. Теория Баклея – Леверетта.

При проектировании разработки и эксплуатации нефтяных и газовых месторождений большое внимание уделяется задачам движения границы раздела двух жидкостей пористой среде. Наиболее разработанной теорией является теория одномерного движения двухфазной жидкости в пористой среде Баклея – Леверетта.

Рассматривая двухфазную фильтрацию в трубке тока постоянного сечения при отсутствии капиллярного давления и без учета массовых сил и пологая, что суммарная скорость фильтрации является постоянной величиной: , Баклей и леверетт получили дифференциальное уравнение относительно σ

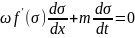(1)

Где m – пористость пласта; - производная от функции Леверетта

где: (2)

Уравнение (1) является квазилинейным дифференциальным уравнением 1-го порядка в частных производных.

Решение уравнения (1) имеет вид:

(3)

Где - координата точки с заданной насыщенностью σ в момент t = 0.

Уравнение (3) определяет перемещение точки с заданной насыщенностью с течением времени.

Скорость распространения заданной насыщенности σ получим из уравнения (3), взяв производную ,

(4)

Баклей и Леверетт из условия материального баланса получили формулу для определения значения фронтовой насыщенности 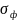(насыщенности на скачке)

(5)

Очевидно, что фронтовую насыщенность можно легко определить графически. Проведя из начала координат касательную к кривой f(σ) (рис. 1) и опустив перпендикуляр из точки касания на ось σ, получим значение фронтовой насыщенности.

Чтобы найти среднее значение насыщенности в переходной зоне, разделим объем поступившей вытесняющей жидкости на объем порового пространства переходной зоны, определяемого координатой при площади поперечного сечения пласта, равной единице

(6)

Среднюю насыщенность можно определить графически следующим образом. Если продлить касательную к кривой f (σ) до пересечения с прямой f (σ) = 1, то значение σ в точке пересечения и есть средняя насыщенность (рис. 1).

Как правило, среднее значение насыщенности порового пространства водой значительно меньше единицы. Поэтому, например, в процессах вытеснения нефти водой для более полного извлечения нефти из пласта на объем добытой нефти нужно закачать несколько объемов воды.