Тема 2.
Лекция 6
Числовые последовательности и ряды
§2.1 Сходящиеся числовые последовательности
Определение 1.
Функция определяющаяся на множестве N и принимающая значения из некоторого множества X, x€R называется числовой последовательностью
Пример 1.
1)
2)
3)
Определение 2.
Числовая последовательность называется сходящейся, если существует такое число Х0, что для любого положительного Е сколь угодно малого, найдется номер члена числовой последовательности, такой, что для всех членов >N будет выполняться неравенство:
- предел числовой последовательности
Если последовательность не сходится ни к какому числу называется расходящаяся
Геометрическая интерпретация
Возьмем Х0 на числовой прямой. Зададим Е и построим Е-окрестность. Из определения следует, что по заданному Е найдется такой N, начиная с которого все члены последовательности будут расположены в этой Е- окрестности. А члены Х1, Х2, ХN – будут лежать за пределами окрестности
Построим отрицание существования предела, то есть
Правило построения отрицания логического выражения:
Замена
и знак неравенства меняется на
противоположный
Пример2.
зададим произвольное
,
найдем N, чтобы выполнилось
неравенство
В качестве
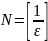Эта функция
целая часть числа
Эта функция представляет целую часть,
х есть наиболее целое число, удовлетворяющее
неравенство
Пример 3.
покажем, что последовательность не
имеет предела (расходится)
От противного, пусть предел существует
Зададим
Тогда, если n- четное, то
если n- нечетное
нет такого , которое удовлетворяет этим неравенствам одновременно. Это противоречие. Значит, предел этой последовательности не существует, значит, она расходится
Пример 4.
Все четные члены стремятся к 0 слева,
а стремятся к +
В любой окрестности точки содержится внутри и за пределами бесконечное число членов числовой последовательности
Теорема 1. (единственность предела)
Если предел последовательности существует, то он единственный
Доказательство:
От противного, предположим, последовательность
,тогда
по определению будет
Возьмем
будут выполняться оба неравенства
одновременно, тогда
- противоречие, двух пределов не может
быть
Определение 3.
Числовая последовательность называется ограниченной, если существует
В противном случае, последовательность называется неограниченной.
Теорема 2.
Всякая сходящаяся последовательность ограничена
Доказательство:
Пусть
- последовательность сходится и
- её редел. Возьмем произвольное
тогда по определению
Обозначим через
Тогда очевидно
Это означает, что последовательность ограничена
Обратное утверждение неверно
она ограничена
- последовательность ограничена, но
она сходится
Пример 5. *
исследовать сходимость последовательности
в зависимости от параметра q
А)
Зададим
По определению для
найдем N
из неравенства
В этом случае сходится
Б)
q=-1 ⇾ Расходится пр. 1
q = 1
В)
Могут принимать любые большие значения, следовательно, последовательность неограниченна и она расходится
Определение 4
Последовательность Хn –
называется неубывающей (невозрастающей)
если
Называются монотонными
Определение 5
Последовательность Хn – называется возрастающей (убывающей) если выполняются условия
называются строго монотонными
Теорема 3.
Всякая монотонная ограниченная последовательность сходится
Доказательство
Пусть Хn– не убывает, по условию Хn– ограничено, то есть её множество значений Х ограничено
Тогда существует точная верхняя грань множества Х
Пусть
тогда по определению
В силу монотонности это неравенство
Добавим в некоторое +
и только усилим неравенство
Это
будет означать, что последовательность
сходится
Лекция 7