2.4 Непрерывность функции

2.4.1 Пусть функция определена в некоторой δ – окрестности точки , в том числе в самой точке . Функция называется непрерывной в точке , если предел функции в точке существует и равен значению функции в этой точке, т.е. .

Функцию называют непрерывной на множестве D, если она непрерывна в каждой точке этого множества.

Условие непрерывности в точке можно записать в эквивалентной форме:

.

Можно ввести приращение функции :

.

Это означает, что условие непрерывности функции в точке эквивалентно выполнению равенства

.

Понятия предела и непрерывности для функции нескольких переменных аналогичны соответствующим понятиям для функции одной переменной, поэтому основные теоремы для непрерывных функций одной переменной остаются справедливыми и для функции нескольких переменных, при этом роль отрезка играет замкнутое множество.

2.4.2 Точка множества, в которой функция не является непрерывной, называется точкой разрыва функции. Точки разрыва могут быть изолированными, образовывать линии разрыва, поверхности разрыва ( для ) и т.д.

Пример. 2.4.2.1Функция непрерывна при любых значениях x и y, т.е. в любой точке плоскости . Действительно, преобразовав функцию

,

найдем приращение функции

,

следовательно,

.

Пример.2.4.2.2 Найти точки разрыва функции

.

Функция не определена в точках, в которых знаменатель обращается в ноль. Поэтому она имеет поверхность разрыва - плоскость .

Заметим, что разрыв в точке , где , можно устранить, положив

= ,

т.е. точка является точкой устранимого разрыва.

Пример.2.4.2.3 Найти точки разрыва функции

.

Заметим, что разрыв в точке , где можно устранить, положив

= ,

т.е. точка - точка устранимого разрыва.

Пример.2.4.2.4 Найти точки разрыва функции

.

Функция определена всюду, кроме точки . Рассмотрим значение z вдоль прямой :

.

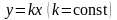Подходя к точке по различным прямым, мы будем получать различные предельные значения, зависящие от k. Это значит, что функция не имеет предела в точке . Функцию нельзя доопределить в этой точке так, чтобы она стала непрерывной. Следовательно, эта точка является точкой неустранимого разрыва.

2.5 Частные производные

2.5.1 Пусть функция определена в некоторой – окрестности точки . Если дать независимой переменной приращение , то функция получит приращение, которое называют частным приращением функции по аргументу и обозначают символом , так что

.

Аналогично определяется частное приращение по :

.

Наконец, сообщив аргументу приращение , а аргументу – приращение , можно получить для новое приращение , которое называется полным приращением функции , определяемое формулой

.

Надо заметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е.

.

Пример.2.5.1 .

.

.

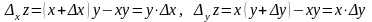Аналогичным образом определяются частные и полное приращения функции любого числа переменных.

2.5.2 Частной производной по (по ) от функции называется предел отношения частного приращения по ( по ) к приращению при стремлении к нулю и обозначается одним из символов

.

Таким образом, по определению,

или

.

Как это видно, правила вычисления частных производных совпадают с правилами, указанными для функций одной переменной, и только требуется помнить, по какой переменной ищется производная.

Частные производные функции любого числа переменных определяются аналогично.

Пример.2.5.2 .

.

Частные производные и , вообще говоря, являются функциями переменных и .

2.5.3 Если у функции (у функции ) существует частная производная по переменной (по переменной ), то ее называют частной производной второго порядка от функции по переменной (по переменной ) и обозначают (и ) или (и ).

Таким образом, по определению:

.

Если существует частная производная от функции (от функции ) по переменной (по переменной ), то эту производную называют смешанной частной производной второго порядка от функции и обозначают символом

.

Как это видно для функции от двух переменных , можно рассматривать четыре производные второго порядка.

Производные второго порядка можно снова дифференцировать как по , так и по . Получим частные производные третьего порядка. Их будет уже восемь:

.

Вообще, частная производная – го порядка есть первая производная от производной –го порядка. Например,

Естественно возникает вопрос, будут ли равны между собой частные производные, если они взяты по одним и тем же переменным одно и то же число раз, но в разном порядке. Например, равны ли

и и ?

В общем случае скажем: если нарушается непрерывность в точке у этих производных, то ответ на этот вопрос отрицательный.

Пример.2.5.3

.

Вычислим частные производные этой функции:

Аналогично вычисляются смешанные производные:

Таким образом, .

2.5.4 Теорема (о смешанных производных)

Пусть функция определена вместе со своими частными производными в некоторой – окрестности точки , причем непрерывны в этой точке, тогда результат дифференцирования не зависит от порядка дифференцирования.

Пример.2.5.4

как видно, .