Метод Ньютона

Відмінність цього ітераційного методу від попереднього полягає в тому, що замість хорди на кожному кроці проводиться дотична до кривої у = f(x) при x = х_i і шукається точка перетину дотичної з віссю абсцис (Малюнок 4). При цьому не обов'язково задавати відрізок [а, b], що містить корінь рівняння (1), досить знайти лише деяке початкове наближення кореня x = х₀.

Застосовуючи метод Ньютона, слід керуватися наступним правилом: як вихідна точка х₀ вибирається той кінець інтервалу [а, b], якому відповідає ордината того ж знаку, що і знак f ˝(х).

Малюнок 3. Метод Ньютона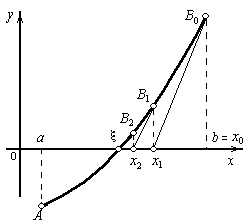

Рівняння дотичної, проведеної до кривої у = f(x) через точку В₀ з координатами х₀ і f(х₀), має вигляд:

Малюнок 5. Ітераційні процеси, що сходяться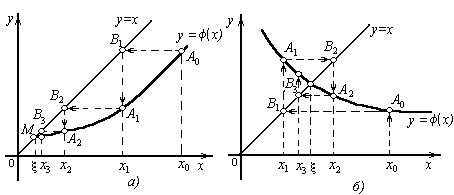

Звідси знайдемо наступне наближення кореня х₁ як абсцису точки перетину дотичної з віссю Ох (у = 0):

Аналогічно можуть бути знайдені і наступні наближення як точки припинення з віссю абсцис дотичних, проведених в точках В₁, В₂ і так далі. Формула для i +1 наближення має вигляд:

(7)

Для закінчення ітераційного процесу може бути використана або умова f(x_i) < , або умова близькості 2х послідовних наближеньx_i – x_{i - 1} < .

Ітераційний процес сходиться якщо

f(х₀)  f  (х₀) > 0.

Малюнок 4. Розв’язання рівняння f(x)= 0 методом Ньютона

Реалізація методу Ньютона засобами MATHCAD приведена на Малюнку 5. Для організації ітераційних обчислень використовується функція until.

until(а, z)

Повертає z, поки вираз а не стає негативним; а повинно містити дискретний аргумент.

Метод простої ітерації (метод простих наближень)

Для використання методу ітерації вихідне нелінійне рівняння f(х)= 0 замінюється рівносильним рівнянням

x = (x).

(8)

Хай відоме початкове наближення кореня х = х₀. Підставляючи це значення в праву частину рівняння (8), отримаємо нове наближення:

х1 = (х0).

Далі, підставляючи кожного разу нове значення кореня в (8), отримуємо послідовність значень:

Рис 6. Ітераційні процеси, що сходяться

(9)

Геометрична інтерпретація:

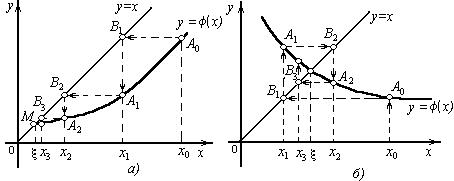
побудуємо на площині xОy графіки функцій у=х і у= (х). Кожен дійсний корінь ξ рівняння (8) є абсцисою точки перетину М кривою у=(х) з прямою у=х(Рис 6, а).

Вирушаючи від деякої точки А₀ [x_0,  (x₀)], будуємо ламану А₀В₁А₁В₂А₂... (“сходи”), ланки якої поперемінно паралельні осі Ох і осі Оу, вершини А₀,А₁,А₂...лежать на кривій у=(х), а вершини В₁,В₂,В₃, - на прямій у=х. Спільні абсциси точок А₁ і В₁, А₂ і В₂ ..., є відповідно послідовними наближеннями х₁, х₂ ... кореня ξ .

М ожливий також інший вигляд ламаної А₀В₁А₁В₂А₂ ... – «спіраль» (Рис 6, б). Розв’язок у вигляді «сходів» виходить, якщо похідна  (х) додатня, а розв’язок у вигляді «спіралі», якщо  (х) від’ємна.

Малюнок 6. Ітераційний процес, що розходиться

На Малюнку 6, а, б крива у= (х) поблизу кореня ξ - полога, тобто , і процес ітерації сходиться. Проте, якщо розглянути випадок, де , то процес ітерації може бути таким, що розходиться (Малюнок 7). Тому для практичного вживання методу ітерації потрібно з'ясувати достатні умови збіжності ітераційного процесу.

Теорема: Нехай функція (х) визначена і диференційована на відрізку [а, b], при чому всі її значення  (х)  [а, b]. Тоді, якщо існує правильний дріб q такий, що q < 1 при а < x < b, то:

1) процес ітерації сходиться незалежно від початкового значення х₀ ( [а, b];

2) граничне значення є єдиним коренем рівняння х=(х) на відрізку [а,b].

Приклад 5. Рівняння

f(x)≡ x3 – x – 1 = 0

(10)

має корінь ξ [1, 2], оскільки f(1)= - 1 < 0 і f(2)= 5 > 0.

Рівняння (10) можна записати у вигляді

х = х3 – 1.

(11)

Тут (х) = х³ – 1 і  (х) = 3х²; тому (х)  3 при 1≤х≤ 2 і, отже, умови збіжності процесу ітерації не виконані.

Якщо записати рівняння (10) у вигляді

(12)

то матимемо: .

Звідси при 1≤ х ≤2 і означає, процес ітерації для рівняння (12) швидко зійдеться.

Знайдемо корінь ( рівняння (10) з точністю до 10^-2. Обчислюємо послідовні наближення х_n з одним запасним знаком по формулі

Знайдені значення поміщені в Таблицю 1:

Таблиця 1

Значення послідовних наближень xi.

i	0	1	2	3	4
xi	1	1,260	1,312	1,322	1,3243

З точністю до 10^-2 можна покласти ξ = 1,324.