14 Вопрос

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданноммножестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Необходимые условия существования локальных экстремумов

• Из леммы Ферма вытекает следующее:

Пусть точка   является точкой экстремума функции  , определенной в некоторой окрестности точки  .

Тогда либо производная   не существует, либо  .

Достаточные условия существования локальных экстремумов

• Пусть функция   непрерывна в 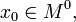  и существуют конечные или бесконечные односторонние производные  . Тогда при условии

 является точкой строгого локального максимума. А если

то   является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке 

• Пусть функция   непрерывна и дважды дифференцируема в точке  . Тогда при условии

 и 

 является точкой локального максимума. А если

 и 

то   является точкой локального минимума.

• Пусть функция   дифференцируема   раз в точке   и  , а  .

Если   чётно и  , то   - точка локального максимума. Если   чётно и  , то   - точка локального минимума. Если   нечётно, то экстремума нет.

15 Вопрос

Определения и понятия.

Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х. Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х. Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой. Посмотрите на чертеж, иллюстрирующий эти определения.

Точка   называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости. Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее. Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной. На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба. 

Необходимое и достаточные условия перегиба.

Сформулируем необходимое условие перегиба графика функции. Пусть график функции y = f(x) имеет перегиб в точке   и имеет при   непрерывную вторую производную, тогда выполняется равенство  . Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения  , в которых вторая производная равна нулю, являются абсциссами точек перегиба. Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все   из области определения функции, для которых   и  . Обычно это точки, в которых знаменатель первой производной обращается в ноль. После того как найдены все  , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции. Пусть функция y = f(x) непрерывна в точке  , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то   является точкой перегиба графика функции. Как видите первое достаточное условие не требует существования второй производной в самой точке  , но требует ее существование в окрестности точки  . Алгоритм нахождения точек перегиба функции. Находим все абсциссы   возможных точек перегиба графика функции (  или  и  ) и выясняем, проходя через какие   вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки   будут точками перегиба графика функции. Рассмотрим два примера для разъяснения. Пример. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции  . Решение. Областью определения функции является все множество действительных чисел. Найдем первую производную:   Областью определения первой производной также является все множество действительных чисел, поэтому равенства   и   не выполняется ни для каких  . 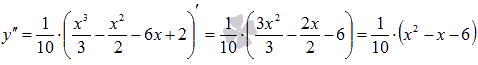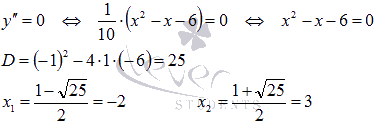Найдем вторую производную:   Выясним при каких значениях аргумента x вторая производная обращается в ноль:   Таким образом, абсциссами возможных точек перегиба являются x = -2 и x = 3.