2. Метод энергетической линеаризации.

В разработанном методе энергетической линеаризации краевой задаче нелинейной теории упругости телу объёма V c границей Г и законом деформирования ставится в соответствие геометрически тождественное гипотетическое линейно-упругое тело с законом деформирования

. (4.11)

Модуль деформации Е^г подлежит определению и должен быть таким, чтобы при тождественных граничных условиях для обоих тел их смещения совпадали.

В силу поставленного условия для модуля деформации Е^г и тождественности граничных условий для рассматриваемых твёрдых тел можно утверждать, что работы внешних сил на смещениях для исследуемого нелинейно – деформируемого и гипотетического линейно-упругого тел будут равны, т.е. будем иметь Wⁿ = W^r, тогда

,

Пⁿ - энергия деформации нелинейно-упруго

П^r - энергия деформации гипотетического линейно - упругого тела; индексы “n” и “r”– признаки нелинейно-упругого и гипотетического линейно - упругого тел.

Полученное выражение представим в следующей форме

, (4.12)

где F( ) = .

В соответствии с основной леммой вариационного исчисления из (4.12) следует:

F( ) - / 2 = 0. (4.13)

При законе деформирования в виде степенной функции из (4.13) получим:

(4.14)

Подставим (4.14) в уравнение состояния (11) и, учитывая закон Гука ,

решим его относительно _i, получим:

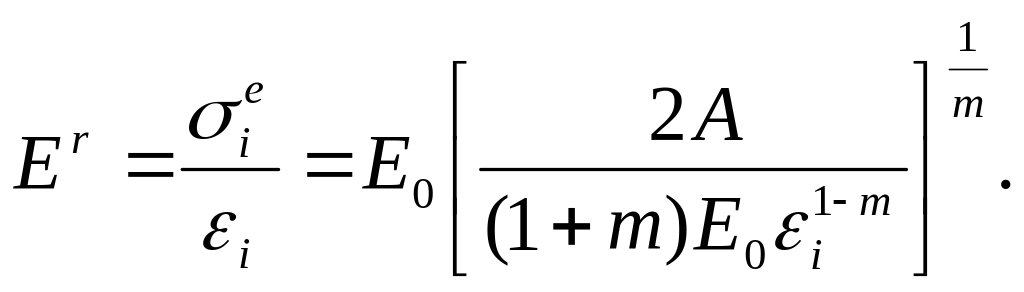
Если закон деформирования имеет вид ,

то определяется из уравнения: E₀ - 2B/(1+m) = , в этом случае

E ^r = / = E₀ - 2B / (1+m) .

Для полученных значений Е^r решается линейная задача. Полученное решение будет являться и решением исходной нелинейной задачи.

3. Технология компьютерного моделирования линейных систем деформируемых твёрдых тел, определённых в односвязной области.

Технология визуального объектно-ориентированного моделирования сложной нелинейной системы деформируемых твёрдых тел основывается на методологии процесса моделирования, содержании и назначении моделируемых задач и может быть представлена следующими основными этапами.

1. .Внешние процедуры;

2. .Внутренние процедуры;

3. .Численное моделирование;

4. .Анализ результатов и принятие решений.

Наполнение этих этапов зависит от содержания моделируемых задач. Рассмотрим содержание процесса компьютерного визуального объектно-ориентированного моделирования систем деформируемых твёрдых тел на примере системы «Фундамент - грунтовое основание».

На этапе внешних процедур анализируются инженерно-геологические показатели грунтового основания, устанавливается область существования и структура системы, определяются параметры дискретизации и физико-механические характеристики элементов основания и конструктивных элементов структур фундаментов, определяются величина и характер распределения внешней нагрузки.

На этапе внутренних процедур производится работа непосредственно с программным обеспечением визуального объектно-ориентированного моделирования заданной структуры фундаментов и грунтовых оснований. При этом формируются вектора для автоматического построения дискретизованной области нерегулярной структуры, создается конкретное наполнение базы данных физико-механических характеристик моделируемой системы, формируются вектора граничных условий для заданной системы, на экране монитора строится виртуальная физическая модель системы, см. рисунок 5.1, каждому конечному элементу системы назначаются его начальные свойства, считываемые из соответствующей базы данных.

На третьем этапе происходит численное решение сформированной задачи. Результаты решения представлены значениями компонент векторов перемещений для каждого узла дискретизованной области при условиях линейного и нелинейного деформирования. Производится экранная визуализация результатов в виде таблиц и графиков.

На четвёртом этапе производится анализ полученных результатов и принимается решение о принятии параметров построенной системы в качестве основного варианта проектируемой физической системы или принимается решение об изменении её структуры и (или) свойств.