Лекция 12. Решение позиционных задач (окончание)

Желающие могут обратится к репетитору:

Буторина Ирина Владимировна. Кафедра графики, ауд. 575. корпус 2, этаж 5

Способ концентрических сфер (окончание)

Задача 4.8_б. Пересечение параболоида вращения с эллипсоидом вращения.

Анализ линии пересечения:

1. Поскольку пересекаются две поверхности второго порядка, то в пересечении образуется пространственная кривая 4-ого порядка. Случай врезки.

2. У поверхностей имеется общая плоскость симметрии, параллельная П₂. Поэтому проекция линии пересечения на П₂ является кривой второго порядка (парабола или гипербола).

3. У поверхностей имеется общая плоскость симметрии, параллельная П₃. Поэтому проекция линии пересечения на П₂ также является кривой второго порядка (часть эллипса).

Особенность задачи в том, что впервые мы встречаемся с параболоидом вращения и эллипсоидом вращения.

Построение параболоида вращения:

1. П 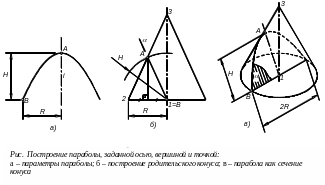остроить параболу как сечение конуса. Парабола задана вершиной, осью точкой (рисунок).

2. Поставить параболу в вертикальное положение вращением.

3. Сформировать контур вращения из полу-параболы и получить параболоид.

Построение эллипсоида вращения. В задаче задан так наз. вытянутый эллипсоид, образованный вращением эллипса вокруг большой полуоси эллипсоид (если вращать вокруг малой оси, образуется сжатый эллипсоид):

1. Построить эллипс по заданным длинам его осей. Построить большую ось.

2. Срезать половину эллипса.

3. Сформировать область из полуэллипса и большой полуоси.

4. Вращать вокруг большой полуоси и получить вытянутый эллипсоид.

Построить модель, автоматизированный чертеж и решить задачу в тетради.

Способ вспомогательных эксцентрических сфер

– применяют для построения линии пересечения поверхностей вращения со скрещивающимися осями. Как и способ концентрических сфер этот способ основан на особенности пересечения поверхностей вращения со сферой по окружностям, которые могут отображаться в прямые линии.

Показать суть способа: файл Лекция 10 "4_10-a_новый.dwg", там же 2d-макет задачи.

Задача 4.9-а – решить в тетради.

Решение задач на частные случаи пересечения поверхностей 2-го порядка

Решение задач на теорему Монжа

Напомнить теорему Монжа: если две поверхности второго порядка касаются третьей поверхности второго порядка, то первые две поверхности пересекаются по двум плоским кривым второго порядка.

Особенность построения 3d-модели задачи: начинать с построения контуров вращения пересекающихся тел и общей касательной сферы, построение должно выполняться с объектной привязкой Касательная и гарантировать касание тел вращения со сферой. Затем из контуров создать тела вращения. Для наглядности можно создать и общую касательную сферу. После пересечения проверить, что полученные линии являются кривыми 2-ого порядка.

Методика есть в конце тетради – разд. 11.5

В полном объеме решить задачу 4.11. Проверить, что получились эллипсы. 3d-модели присвоить прозрачный материал и увидеть сферу. Можно показать файл: лекция 10 "Монж с решением 4-11.dwg". Решить задачу в тетради.

Задачи на двойное соприкосновение

Напомнить теорему о двойном соприкосновении. Повторить построение модели 4_11-a (Лекция 11). Решить задачу в тетради.

Задачи при наличии общей линии 2-го порядка в пересечении

Теорема. Задача 4_13-б. Решить в полном объеме. Модель в файле лекция 11 "4_13-б.dwg". Модель начинать с построения общей линии. Построить, доказать получение эллипса. Решить в тетради.