3. Модели неэквидистантных временных рядов

Рассмотрим типовые модели неэквидистаптпых временных рядов, широко применяемых па практике как при описании, так и при метрологическом анализе алгоритмов оценивания вероятностных характеристик иеэквидистаитиых временных рядов. На практике, при описании различных видов неравномерной дискретизации, приводящей к нерегулярным временным рядам, как правило, применяют модели рекуррентных потоков Пальма:

• периодической дискретизации со случайными пропусками наблюдений;

• периодической дискретизации с «дрожанием»;

• аддитивной случайной дискретизации;

• периодической дискретизации с «дрожанием» и пропусками наблюдений;

• аддитивной случайной дискретизации с пропусками наблюдений.

Для аддитивной случайной дискретизации

(1)

где - последовательность независимых случайных величин с плотностью распределения вероятностей , каждая из которых расположена в диапазоне (0, ). Интервал дискретизации для этой модели равен

(2)

Учитывая, что в практике широко применяется модель простейшего потока и по тока с распределением интервалов, подчиненного гамма-распределению, частным случаем которого являются законы Эрланга, экспоненциальное, вырожденное причинное, показательно степенное, Пирсона и т.д., определим их характеристики.

4. Моделирование сп

Для решения задачи моделирования ПСП с заданным законом распределения случайный процесс подвергается нелинейному преобразованию. Теоретической базой для определения вида и характеристик нелинейной функции является теория функций случайного аргумента.

Допустим, случайная величина X имеет плотность распределения вероятности , а необходимо получить выходную величину Y с плотностью распределения вероятностей . Таким образом, мы должны определить вид нелинейной функции преобразования у = g(х).

Известно, что

. (3)

Отсюда

(4)

Допустим, что обратная функция преобразования

(5)

Тогда

(6)

Если в качестве входной ПСП выбрать «белый шум» с /" , то х = {(у)=Р_у(у), (2.8)

Отсюда можно определить вид нелинейной функции преобразования у = ₈(х)=Г;¹(х). (2.9)

Графическая интерпретация метода инверсного преобразования представлена на рис. 2.3.

Рисунок 2.3 - Моделирование ПСП с заданным видом закона распределения вероятностей

Обычно можно найти аналитическое решение Р_у ¹(х) только для ограниченного числа случаев. Примеры интегральных функций распределения и обратных им функ­ций приведены в приложении П.З.

K_x(τ) = M[Ẋ(t) Ẋ(t + τ)].

5. Статистическая оценка характеристик сп

Для любой дискретной СВ X – числовая функция F(x) = Р(Х < х), -∞ < х < +∞ называется функцией распределения (ФР) этой СВ, а функция f(х) = F'(x), называется плотностью распределения или плотностью вероятности (ПВ) этой СВ.

Приведем графики возможных ФР F(x) и ПВ f(х) при равномерном законе распределения.

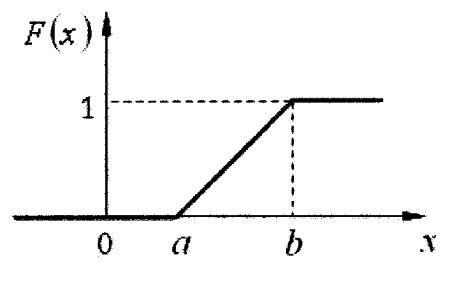
Рисунок 4 – Функция распределения при равномерном законе

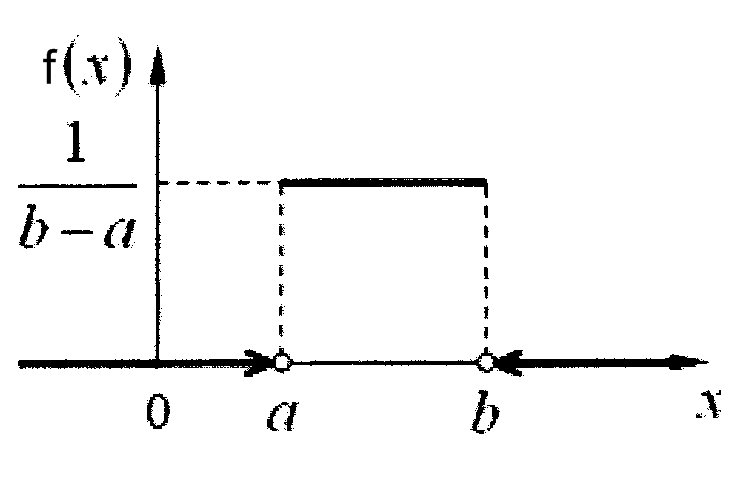
Рисунок 5 – Плотность вероятности при равномерном законе

ФР любой случайной величины обладает следующими свойствами:

• F(x) определена на всей числовой прямой R;

• F(x) не убывает, т.е. если x₁ ≤ x₂, то F(x₁) ≤ F(x₂);

• F(-∞)=0, F(+∞)=1, т.е. и

• F(x) непрерывна справа, т.е. .

ПВ любой случайной величины обладает следующими свойствами:

• плотность распределения – неотрицательная функция f(x) ≥ 0;

• несобственный интеграл от плотности распределения в пределах от - ∞ до +∞ равен единице:

Рассмотрим основные числовые характеристики СП.

Математическое ожидание – мера среднего значения случайной величины, определяется формулой:

Дисперсия случайной величины – мера разброса данной случайной величины, то есть её отклонения от математического ожидания:

Абсолютны центральны момент k-го порядка СВ X:

Коэффициент ассиметрии – числовая характеризующая степени несимметричности распределения СВ:

Коэффициент эксцесса – числовая характеризующая степени остроты пика распределения СВ:

Для коэффициента ассиметрии и эксцесса Ẋ – среднее значение: