Классификация потоков событий
В системах реального времени обработки и передачи информации, управления наблюдаются различные потоки событий. Поток событий представляет собой точечный процесс с событиями, появляющимися случайным или периодическим образом во времени.
Различают потоки однородных и неоднородных событий. Например, в системах связи, реализующих приоритет определенной группы абонентов, поток вызовов будет с этой точки зрения неоднородным, система по-разному будет реагировать на разные события (вызовы) в потоке. На рассматриваемые же события (отсчеты первичного процесса) реакция устройств АСНИ, дискретных ИИС, как правило, не меняется при изменении порядкового номера события и поэтому поток выборок можно считать однородным.
Основными характеристиками, классифицирующими случайный поток, являются свойства стационарности, ординарности и последствий.
Стационарным
называется поток событий, для которого
вероятность
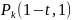появления какого-либо числа k
событий на определенном интервале
времени
зависит лишь от значения этого интервала
t и не зависит от его
расположения на оси времени.
Ординарным называется поток, для которого вероятность появления на малом участке δt, примыкающем к произвольно выбранному моменту времени, более одного события пренебрежимо мала по сравнению с вероятностью появления хотя бы одного события.
Последействие
потока заключается в зависимости
вероятности
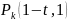от распределения событий на оси времени
вне интервала
.
Либо, другими словами, поток не обладает
последействием, если вероятность
появления на любом интервале времени
какого-либо числа событий не зависит
от того, сколько событий произошло на
других, не перекрывающихся с данным
интервалом. Из литературы известно, что
не обладает последействием только
простейший случайный или иначе
стационарный пуассоиовский поток,
имеющий экспоненциальное распределение
интервалов времени между событиями в
потоке.
Варьируя этими свойствами, можно образовывать различные классы потоков:
простейший поток ‑ поток Пуассона, обладающий всеми тремя свойствами, наиболее широко применяемый на практике;
рекуррентные потоки, относящиеся к классу стационарных потоков Пальма, у которых одномерные законы распределения интервалов дискретизации одинаковы, а сами интервалы независимы между собой;
поток смены состояний марковского процесса Вольда, предполагающий зависимость соседних интервалов между событиями в потоке;
альтернирующие потоки, у которых плотность распределения интервалов чередуется от интервала к интервалу (выбирается из двух возможных видов);
модель рекуррентного потока, получаемого разряжением посредством p-преобразования исходного потока (каждое событие с вероятностью р остается в потоке, а с вероятностью
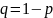выбрасывается.
Выбор модели потока зависит от характера решаемой задачи, метода исследований (аналитический или имитационное моделирование) и т.д. При аналитических исследованиях предпочтение следует отдавать простейшим моделям, позволяющим получить сравнительно простые выражения, удобные для инженерного расчета основных параметров алгоритмов.