4. Модуль іi. Застосування математичних моделей для

оптимізації технічних систем

Змістовий модуль 3. Основи теорії оптимізації.

Тема 1: Загальна постановка і види задач прийняття рішень.

Постановка і види задач прийняття рішень. Математична постановка завдання оптимізації. Цільова функція. Задачі мінімізації і максимізації.

Тема 2: Математична постановка задачі прийняття рішень.

Локальний і глобальний мінімум (максимум) цільової функції. Розв’язуваність завдань оптимізації. Задача математичного програмування. Методи вирішення задач оптимізації математичних моделей.

Змістовий модуль 4. Методи розв’язування задач оптимізації з використанням математичних моделей.

Тема 1: Графо-аналітичний метод розв’язування задач оптимізації математичних моделей.

Постановка задачі. Побудова області допустимих розв’язків задачі оптимізації. Знаходження в межах області допустимих розв’язків оптимального рішення.

Тема 2: Чисельні методи розв’язку задач нелінійного програмування

Класифікація чисельних методів вирішення завдань нелінійного програмування. Класичний метод.  Метод направленого перебору. Метод золотого січення.

Тема 3: Методи вирішення багатокритерних задач оптимізації.

Метод пошуку Парето - ефективних рішень. Метод вирішення багатокритерних завдань оптимізації з використанням узагальненого (інтегрального) критерію. Адитивний критерій.

5. Теоретичні відомості

Проектування пакувальних автоматів (ПА) на функціонально-модульному рівні полягає в проведенні його синтезу із закінчених функціональних елементів – функціональних модулів (ФМ). При цьому проектований ПА, як правило, не може бути описаний однокритеріальною залежністю, тому при оцінці його якості необхідно звертатися до пошуку деякого комплексного показника. Для вирішення цього завдання застосовуються методи розв’язання багатокритеріальної задачі оптимізації, зокрема методи направленого перебирання варіантів, одним з яких є метод віток і меж.

В основі алгоритму пошуку найкращого варіанта структури методом віток і меж лежить ідея послідовного поділу множини допустимих розв’язків на підмножини. Перебирання здійснюється таким чином, щоб відхилити неперспективні розв’язки із множини всіх існуючих без їх безпосередньої перевірки, розглядаючи більш детально лише частину можливих розв’язків. При цьому розв’язується задача мінімізації або максимізації деякої цільової функції F. Значення цільвої функції на першому кроці оптимізації F₀ задає верхню межу оцінки для всіх майбутніх допустимих значень. Якщо оцінка знизу не менше рекорду – найкращого із знайдених рішень – то підмножину можна відхилити. Підмножину можна відхиляти ще й тоді, коли не вдається знайти найкраще рішення. Якщо значення цільової функції на знайденому варіанті рішення менше, ніж попередній результат, то відбувається зміна рекорду. Оптимальний розв’язок х_опт є результатом роботи алгоритму, тобто його рекордом (рис. 1).

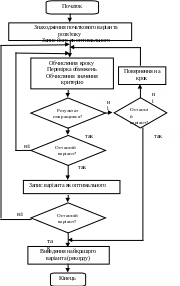
Рис. 1. Блок-схема направленої оптимізації варіанта структури

методом віток і меж

В загальному випадку математичне формулювання даної задачі оптимізації має вид:

, (1)

де критерієм є функція

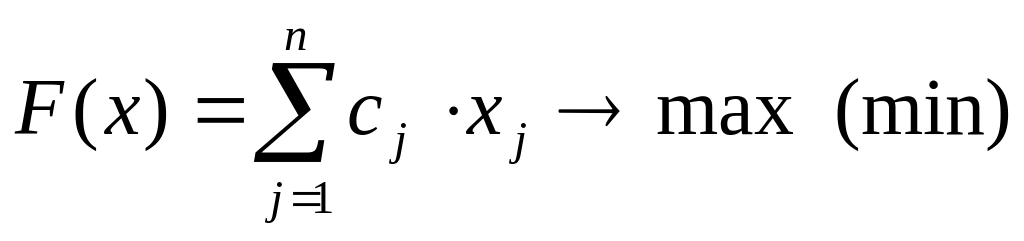. (2)