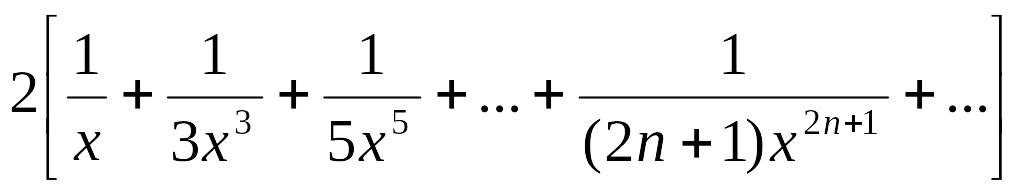3.3.Задание для индивидуальной работы

Разработать алгоритм и программу, определяющие сумму ряда с заданной погрешностью (ипсилон) для произвольно заданного аргумента x. Определить число повторений итерационного цикла.

Вариант	Бесконечная сумма	Диапазон изменения х	Выражение для проверки
1			ex
2			cos x
3
4			sin x
5
6
7
8			ax
9			-ln(1-x)
10
11
12
13			ln(1+x)
14			Lnx
15			arctg(x)
16
17	1+x+x2+x3+…+xn+…
18	1+xcosx+x2cos2x+…+xncosnx+…
19
20
21	xsinx+x2sin2x+…+sinnx+…
22	1-(1-x)+(1-x)2-(1-x)3+…+(-1)n(1-x)n+…
23	1-x+x2-x3+…+xn+…
24	1+2x+3x2+4x3+…+nxn-1+…
25	X+x3+x5+…+x2n+1+…

3.4.Пример выполнения задания

Рассмотрим задачу вычисления функции y=cos(x) с погрешностью _{,используя разложение косинуса в ряд}

Накопление суммы производим по рекуррентной формуле

S_n=S_n-1+t_n(x)

Текущий член ряда будем вычислять по формуле

На рис. 2.1 приведён алгоритм вычисления бесконечного ряда с заданной погрешностью eps.

Рис. 2.1. Алгоритм вычисления суммы бесконечного ряда

Программа вычисления суммы имеет следующий вид:

{Цель: вычисление суммы с заданной погрешностью по }

{ итерационному алгоритму }

{Переменные:x-аргумент функции,S-сумма }

{ eps-погрешность вычисления суммы }

{ n-переменная суммирования }

{ t- слагаемое }

program symma;

var

eps,S,t,x:real;

n:integer;

Begin

{ввод исходных данных}

Writeln('введите x, погрешность eps');

Read(x,eps);

Writeln('для x= ',x:6:2,' с погрешностью ',eps:6:4);

t:=1;

S:=1;

n:=1;

while abs(t)>eps do {начало цикла}

begin

t:=-t*x*x/(2*n*(2*n-1));

S:=S+t;

n:=n+1;

end; {конец цикла}

Writeln('n= ',n,'S= ',S:7:4);

Writeln('контрольное значение = ',cos(x):7:4);

end.