1.7 Уравнение прямой в отрезках на осях координат:

	. (11) Эта прямая (рис.24) отсекает на оси Ох отрезок длиной а, а на оси Оу – длиной в. Действительно, легко убедиться, что она проходит через точки с координатами (а, 0) и (0, в).
рис.24

2.Уравнения плоскости

Перечислим основные уравнения, задающие плоскость.

2.1 Уравнение плоскости, проходящей через данную точку М₀(x₀, y₀, z₀) перпендикулярно её вектору нормали (выводится аналогично уравнению прямой 1).

А·(х – х0) + В·(у – у0) + С·(z – z0)= 0,		(12)
	где А, В, С – координаты её вектора нормали , а (x0, y0, z0) – координаты точки, лежащей на плоскости (рис.25)
рис.25

Если в уравнении (12) раскрыть скобки и обозначить постоянную величину -А·х₀ - В·у₀ - С·z₀ через D, получим:

2.2 Общее уравнение плоскости.

Ах + Ву + Сz + D= 0,

(13)

где А, В и С есть координаты её вектора нормали (А² + В² + С² ≠ 0).

2.3 Уравнение плоскости в нормальной форме.

х·cos α + y·cos β + z·cos γ – p = 0,

(14)

где cos α, cos β cos γ и – координаты единичного вектора нормали плоскости, р – расстояние от начала координат до плоскости. Выводится аналогично уравнению (8) с помощью рис.23 на котором под L , будем подразумевать плоскость.

2.4 Уравнение плоскости в отрезках на осях координат.

,

(15)

где а, в, с – отрезки, отсекаемые плоскостью соответственно на осях Ох, Оу и Оz.

2.5 Уравнение плоскости проходящей через три заданные точки М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂) и М₃(x₃, y₃, z₃).

(16)

	Уравнение (16) представлено в координатной форме, однако его можно записать и через векторы (например, радиус-векторы). Еще из школьного курса мы знаем что, три точки однозначно определяют плоскость.
рис.26

Составим вектора по этим точкам (рис.26). Данные вектора компланарны, а значит их смешанное произведение равно нулю. Записанное в координатной форме смешанное произведение и даст уравнение (16).

2.6 Уравнение пучка плоскостей.

А1х + В1у + С1z + D1 + λ·( А2х + В2у + С2z + D2) = 0,

(17)

при произвольном значении λ определяет некоторую плоскость γ, проходящую через прямую пересечения плоскостей α: А₁х + В₁у + С₁z + D₁ = 0 и β:А₂х + В₂у + С₂z + D₂ = 0 (рис.27).

рис.27

Здесь же добавим следующие формулы, которые могут понадобиться при решении задач.

Расстояние от точки М₀(x₀, y₀, z₀) до плоскости определяемой уравнением (13), находится по формуле:

d = .

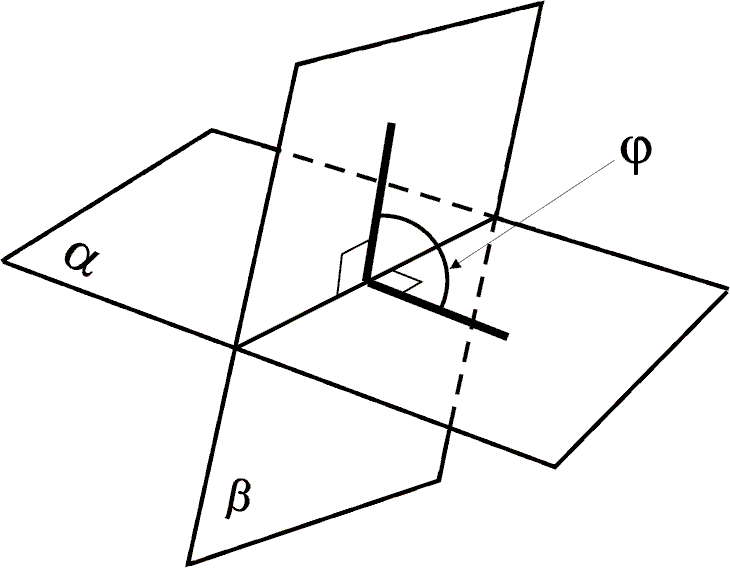
	Расстоянием от точки до плоскости является длина перпендикуляра опущенного из данной точки на плоскость (рис.28). Угол между плоскостями есть величина линейного угла (меньшего) между перпендикулярами опущенными (каждый в своей плоскости) к линии пересечения плоскостей рис.29.
рис.28
рис.29

Угол между плоскостями α: А₁х + В₁у + С₁z + D₁ = 0 и β: А₂х + В₂у + С₂z + D₂ = 0 определяется по формуле:

cos φ = .