3. Длина и направление вектора.

Как следует из определения, вектор характеризуется величиной и направлением. Рассмотрим вопрос о том, как их определить, зная координаты вектора.

Длина вектора через его координаты (проекции) выражается следующей формулой:

, где

а_х, а_у, a_z – координаты (проекции) вектора на оси Ох, Оу, Оz.

В одномерном случае (когда две проекции вектора равны нулю) длина вектора равна величине третьей ненулевой проекции, взятой по модулю. При этом вектор коллинеарен одной из осей координат.

Пример. Найти длину вектора {0, -4, 0}.

Решение. = = 4.

В двумерном случае (когда только одна координата вектора равна 0) формула совпадает с формулой из теоремы Пифагора. Пусть, к примеру, а_х = 0, тогда . При этом вектор лежит либо в плоскости уОz, либо в плоскости, параллельной ей.

рис.15

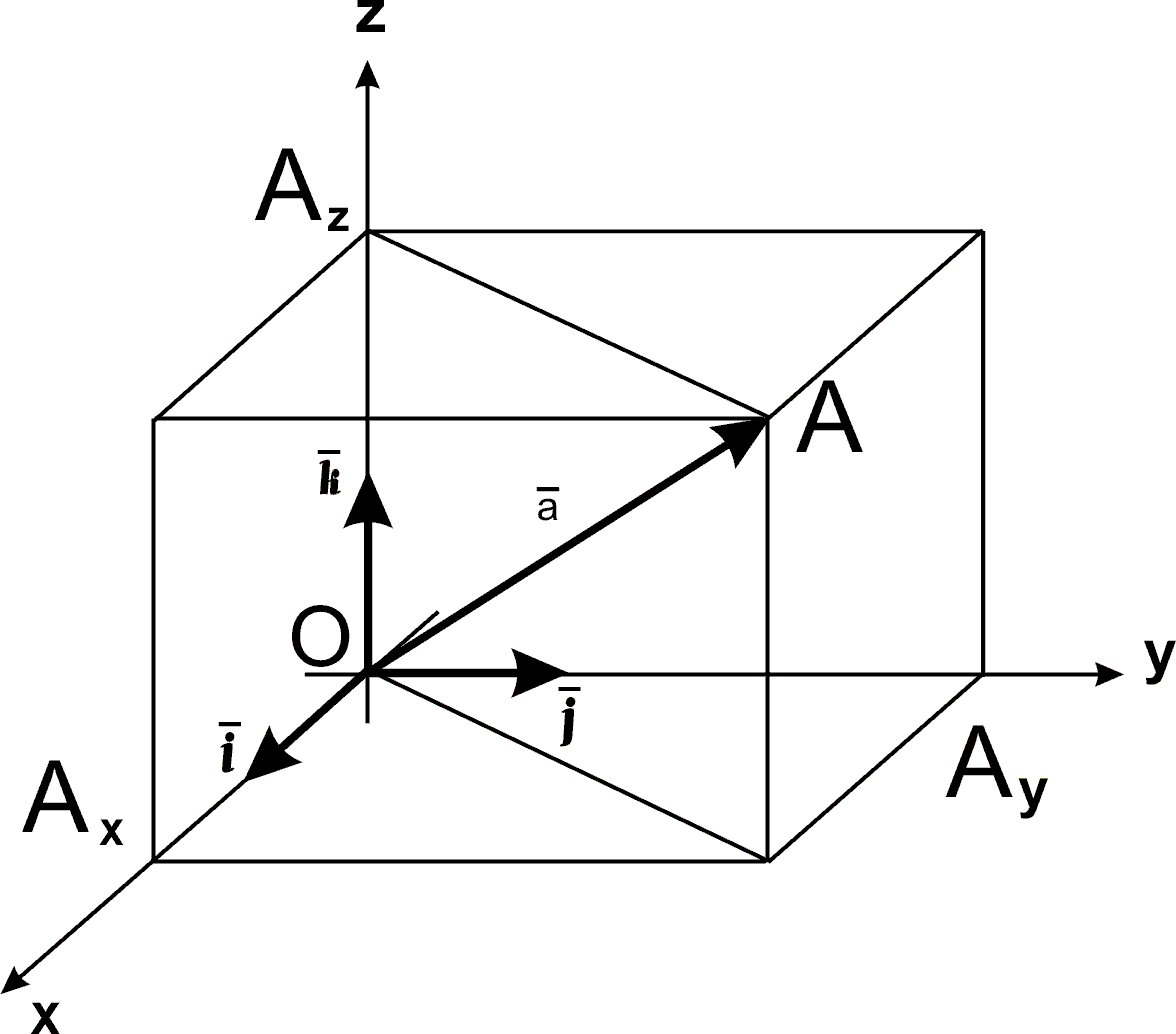
В трехмерном случае (когда все три проекции вектора отличны от нуля) всегда можно построить такой прямоугольный параллелепипед с ребрами, параллельными осям координат и тремя измерениями, соответственно равными а_х, а_у, a_z, у которого вектор занимает положение одной из четырех диагоналей, и совпадает с ними по величине, определяемой аналогичной формулой (рис.15).

Таким образом, длина вектора = {x₂ – x₁; y₂ - y₁; z₂ - z₁} может быть найдена также по формуле:

.

Эту же формулу можно использовать для определения расстояния между двумя точками, взяв эти точки в качестве начала и конца вектора .

Направление вектора задается косинусами углов, образованных вектором с осями координат. Чтобы их найти, необходимо заданный координатами вектор разделить на его длину:

.

Координаты единичного вектора, того же направления что и вектор , и дают значения косинусов углов между вектором и осями координат. Они называются направляющими косинусами. Действительно, проекции единичного вектора, как и проекция любого вектора, равна произведению длины вектора на косинус угла между ним и осью, на которую проектируется этот вектор. Но длина единичного вектора равна единицы. Поэтому проекции единичного вектора совпадают с косинусами соответствующих углов.

Пример.

Определить длину и направление вектора {1, -3, 2}.

Решение. 1. = = .

2. cos α = ; cos β = ; cos γ = .

Для направляющих косинусов должно выполняться равенство: cos² α + cos² β + cos² γ = 1.

4. Скалярное произведение векторов.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними:

(т. е. результатом векторного произведения является число).

Учитывая определение проекции вектора, скалярное произведение двух векторов можно сформулировать как произведение длины одного вектора на проекцию на него другого вектора.

Перечислим основные свойства скалярного произведения:

1. (т. к. в этом случае φ = 0 => cos(φ) = 1)

2. = 0, если = 0, либо = 0, либо .

3. =

4. 

5. 

Из свойства б следует условие перпендикулярности двух векторов: два ненулевых вектора перпендикулярны, если их скалярное произведение равно нулю (справедливо и обратное утверждение).

Пусть даны два вектора в виде разложения по ортам = х₁ + у₁ + z₁ и = х₂ + у₂ + z₂ . Тогда, перемножая их скалярным образом, мы получаем

= х₁ х₂ + у₁ у₂ + z₁ z₂.

т.е. выражение скалярного произведения двух векторов через их координаты.

Теперь, исходя из определения скалярного произведения, можно записать выражение косинуса угла между двумя векторами через их координаты:

= =

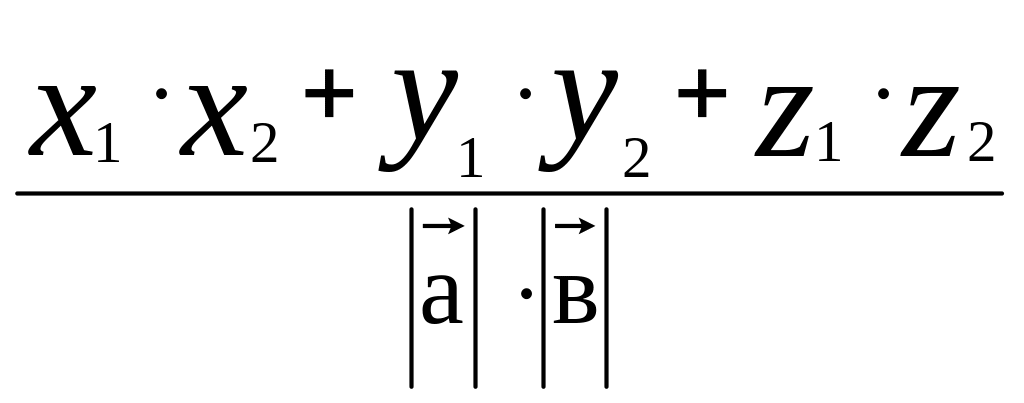Пример. Даны два вектора

и .

При каком значении m эти векторы перпендикулярны?

Решение. Два вектора перпендикулярны, если их скалярное произведение равно нулю. Перемножим скалярно векторы и заданные в координатной форме:

m·4 + 3·m – 4·7 = 0. Данное равенство выполняется при m=4.

Ответ: векторы перпендикулярны при m=4.