Ф ЕДЕРАЛЬНОЕ АГЕНСТВО

ПО КУЛЬТУРЕ И КИНЕМАТОГРАФИИ

Федеральное государственное образовательное учреждение

высшего профессионального образования

"Санкт-Петербургский государственный

университет кино и телевидения"

__________________________________________________________________________

Кафедра математики и информатики

ЭЛЕМЕНТЫ

ВЕКТОРНОЙ АЛГЕБРЫ

И

АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Методические указания к выполнению

расчетно - графической работы для студентов

очного и заочного отделения факультетов АВТ и ПСКТ

САНКТ- ПЕТЕРБУРГ

2008

Составители: доцент Самигулин И. З.,

ст. преп. Меркушин А. В.

ст. преп. Заремская Е. А.

Рецензент: доцент Бегун Е. Н.

Рекомендовано к изданию в качестве методического пособия кафедрой математики и информатики для студентов факультетов АВТ и ПСКТ для очного и заочного отделения.

Протокол № от г.

1. Санкт-Петербургский государственный университет кино и телевидения, 200 г.

Введение

Настоящие методические указания предназначены для студентов как очного, так и заочного отделения факультетов АВТ и ПСКиТ Санкт-Петербургского университета кино и телевидения. Они призваны помочь студентам справиться с решением расчетно-графической работы (РГР) “Пирамида”, задания к которой приведены в конце данных методических указаний, а так же с решением задач по теме “Элементы векторной алгебры и аналитической геометрии”. Овладение этими разделами математики вызвано потребностями в них механики, физики, оптики и ряда других спецдисциплин. Многие важные понятия физики и механики (скорость, ускорение, сила, момент) являются векторными величинами. Именно в соответствии с потребностями физики приходится рассматривать абстрактный вектор и операции над векторами. Операции над абстрактными векторами явились естественным обобщением операций над величинами, рассматриваемыми в физике. На базе векторной и линейной алгебры построена аналитическая геометрия. Развитие векторной алгебры было связанно с развитием векторного и тензорного анализа. Все это обусловило прогресс в развитии математики и её приложений к естественным наукам.

В настоящие методические указания включены такие раз­делы как: векторы и линейные операции над векторами, поня­тие базиса, скалярное, векторное и смешанное произведения векторов, плоскость, прямая.

Векторная алгебра

1. Векторы. Линейные операции над векторами.

Вектором называется направленный отрезок прямой, заданной длины. Направление вектора (от начала к концу) на

рис.1

рисунках указывается стрелкой (рис.1). Если на плоскости или в пространстве точка А является началом вектора, а точка В – его концом, то сам вектор обозначается символом или одной строчной буквой, например , а его длина (модуль, величина вектора) - или . Если = 1, то вектор называется единичным и обозначается . При совпадении точек А и В вектор называется нулевым вектором. Нулевой вектор не имеет определенного направления, а его длина, соответственно, равна нулю.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если при этом их направления совпадают, то они называются сонаправленными ( ), например, рис.2 и рис.3. Если нет – противоположно направленными ( ), рис.4.

рис.2
рис.3	рис.4

Векторы, лежащие в одной плоскости или расположенные на прямых, параллельных одной и той же плоскости, называются компланарными.

Векторы называются равными, если они сонаправлены и их длины равны, т. е. если и . От любой точки, в том числе и от начала координат, можно отложить вектор равный данному и при том только один. Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены (рис.5).

рис.5

Суммой двух векторов и называется третий вектор

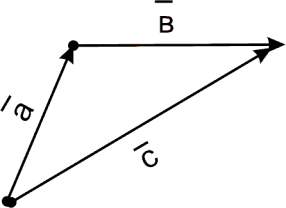
рис.6

, который идет из начала вектора в конец вектора при условии, что начало вектора совпадает с концом вектора (правило треугольника). Построение суммы изображено

на рис.6. Следует заметить, что начало вектора всегда может быть совмещено с концом вектора при помощи параллельного переноса (рис.7).

рис.7

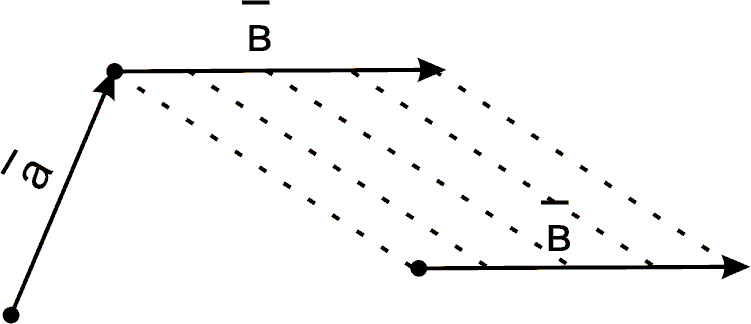
Наряду с правилом треугольника часто пользуются, равносильным ему, правилом параллелограмма: если векторы и

рис.8

приведены к общему началу и на них построен параллелограмм (см. рис.8), то сумма есть вектор, совпадающий с диагональю, идущей из общего начала этих векторов. Общее правило сложения векторов

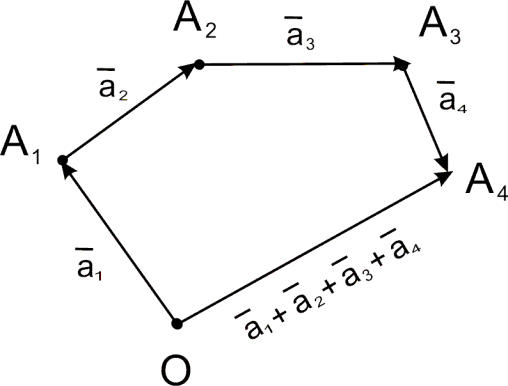
(правило многоугольника): чтобы построить сумму векторов нужно начало второго вектора совместить с концом первого вектора , начало третьего – с концом второго и т. д. Суммарным будет вектор, соединяющий начало первого вектора с концом последнего. На рис.9 приведен, в качестве примера, случай для n = 4.

рис.9

Разностью двух векторов и называется вектор, который в сумме с вектором составляет вектор .

В качестве примера можно обратиться к рис.6, где вектор будет являться разностью векторов и .

Вычитание двух векторов и можно представить через сложение вектора и вектора обратного вектору , т. е.:

= .

Произведением вектора на вещественное число к называется такой вектор , который удовлетворяет следующим требованиям:

1. ,

2. коллинеарен ,

3. и сонаправлены, если к > 0 и противоположно направлены, если к < 0. При к = 0, = 0.

На рисунках 10 и 11 приведены случаи умножения положительного к на вектор .

0 < к < 1	к > 1
рис.10	рис.11

В частности, если к = 1 / , то полученный вектор будет иметь длину равную единице и направление его совпадет с направлением вектора , т. е. мы получаем = / . Нахождение называется нормированием вектора.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.