И соответствующая ей магнитная схема замещения (б)

Расчет магнитных схем замещения производится с помощью законов Ома и Кирхгофа для магнитных цепей.

З а к о н о м а действует для ветвей магнитных цепей, вытекает из соотношений (5.8) и (5.10) и записывается математически в виде следующих равенств:

, (5.12)

. (5.13)

В словесной формулировке закон Ома для магнитных цепей звучит так: падение магнитного напряжения ветви магнитной цепи прямо пропорционально магнитному потоку этой ветви, а коэффициентом пропорциональности является магнитное сопротивление ветви.

П е р в ы й з а к о н К и р х г о ф а д л я м а г н и т н ы х ц е п е й формулируется следующим образом: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.

Математически первый закон Кирхгофа записывается так:

, (5.14)

где , i = 1, , n – мгновенное значение магнитного потока i-й ветви, подключенной к рассматриваемому узлу.

Для переменных магнитных полей первый закон Кирхгофа при условии, что величины , i = 1, , n, изменяются по закону гармонических колебаний, записывается так:

, (5.15)

где , i = 1, , n – комплексный магнитный поток i-й ветви, подключенной к рассматриваемому узлу.

Первый закон Кирхгофа для магнитных цепей следует, как это нетрудно показать, из принципа непрерывности магнитного потока (5.1).

В т о р о й з а к о н К и р х г о ф а д л я м а г н и т н ы х ц е п е й формулируется следующим образом: алгебраическая сумма падений магнитных напряжений, действующих на всех участках замкнутой магнитной цепи, равна алгебраической сумме всех МДС, действующих в этой же цепи.

Математически второй закон Кирхгофа записывается так:

, (5.16)

где – мгновенное значение падения магнитного напряжения на i-м участке рассматриваемой замкнутой магнитной цепи; n – количество всех участков, на которые разбита рассматриваемая замкнутая магнитная цепь; – мгновенное значение j-й МДС, действующей на одном из участков рассматриваемой замкнутой магнитной цепи; m – общее количество МДС, действующих в рассматриваемой замкнутой магнитной цепи.

Для переменных магнитных полей второй закон Кирхгофа при условии, что падения магнитных напряжений и МДС изменяются по закону гармонических колебаний, записывается так:

, (5.16)

где – комплексное падение магнитного напряжения на i-м участке рассматриваемой замкнутой магнитной цепи; n – количество всех участков, на которые разбита рассматриваемая замкнутая магнитная цепь; – j-я комплексная МДС, действующая на одном из участков рассматриваемой замкнутой магнитной цепи; m – общее количество МДС, действующих в рассматриваемой замкнутой магнитной цепи.

Второй закон Кирхгофа следует, как это нетрудно показать, из закона полного тока (1.12).

Рассмотрим пример составления уравнений по законам Ома и Кирхгофа для магнитной схемы замещения, представленной на рис. 5.5, б.

Согласно первому закону Кирхгофа для магнитных цепей можно записать следующее уравнение для верхнего узла:

. (5.17)

По второму закону Кирхгофа с учетом закона Ома можно составить для двух замкнутых контуров, обходя их по часовой стрелке, два следующих уравнения:

, (5.18)

. (5.19)

В последних трех уравнениях неизвестны три магнитных потока: . Решая три указанных уравнения с тремя неизвестными потоками при условии, что магнитные сопротивления являются постоянными величинами, нетрудно определить магнитные потоки. Эту задачу следует решить САМОСТОЯТЕЛЬНО.

Если учесть ответвление магнитных потоков в воздух, то магнитная схема замещения для рассмотренной выше магнитной цепи (см. рис. 5.6, а) примет более сложный вид. Прежде чем составить такую схему замещения введем ряд понятий.

Ферро- или ферримагнитный участок магнитной цепи с обмоткой называют с т е р ж н е м, а без обмотки – я р м о м.

Воздушный промежуток внутри стержня или ярма, имеющий относительно небольшую длину, называют в о з д у ш н ы м з а з о р о м.

Внутренний объем магнитной цепи (см. рис. 5.6, а), не содержащий ферро- или ферримагнитное вещество и не являющийся воздушным зазором, называют о к н о м.

Магнитные потоки, ответвляющиеся в окна и во внешний объем, окружающий магнитную цепь (кроме воздушных зазоров), называют м а г -н и т н ы м и п о т о к а м и р а с с е я н и я.

Можно показать, опираясь на соотношение (5.2), что магнитные потоки рассеяния в реальных магнитных цепях существенно меньше магнитных потоков, действующих в ферромагнитных частях магнитных цепей.

Можно показать также, что магнитный поток воздушного зазора равен магнитному потоку стержня или ярма, продолжением которых этот зазор является. Для этого следует записать принцип непрерывности магнитного потока для замкнутой поверхности, охватывающей границу раздела воздушного зазора и магнитного материала, и допустить, что магнитный поток через боковые участки этой поверхности равен нулю. Возможность такого допущения следует обосновать и записать требуемые математические выкладки САМОСТОЯТЕЛЬНО.

Возвратимся к составлению магнитной схемы замещения магнитной цепи (см. рис. 5.6, а), которая учла бы ответвление магнитных потоков или, иначе говоря, магнитных потоков рассеяния этой магнитной цепи. При построении магнитной схемы замещения будем полагать, что в данной магнитной цепи существует три потока рассеяния: поток рассеяния левого окна , поток рассеяния правого окна и поток рассеяния воздушного внешнего объёма . Будем полагать также, что все потоки сходятся в одном узле. То есть будем считать, что магнитные потоки рассеяния ответвляются только в области междуоконного ярма, по которому проходит магнитный поток Ф_3. Тогда схема замещения рассматриваемой магнитной цепи примет вид, представленный на рис. 5.7. Здесь – магнитные сопротивления соответственно первого и второго окон и воздушного внешнего объема, окружающего магнитную цепь.

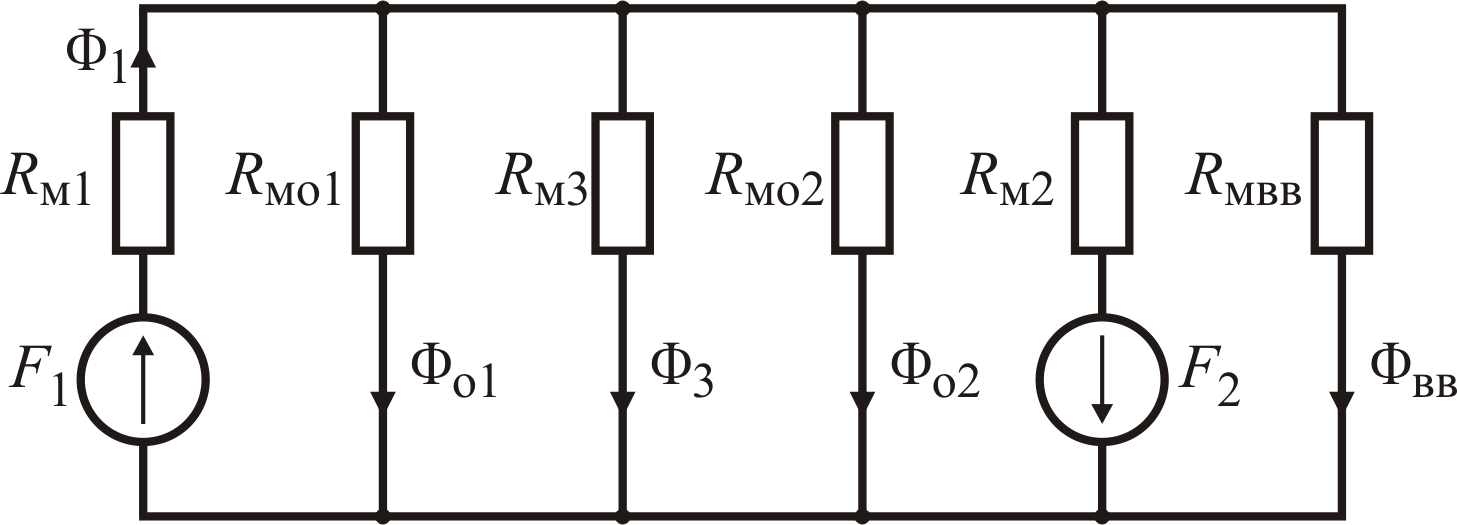
Рис. 5.7. Магнитная схема замещения магнитной цепи (см. рис. 5.6, а) с учетом магнитных потоков рассеяния

Расчет магнитной схемы замещения представляет собой относительно простую задачу в том случае, если можно считать магнитные сопротивления постоянными величинами. Тогда система уравнений, описывающая магнитную схему замещения, представляет собой систему линейных уравнений, для численного решения которой существует ряд методов, например, метод исключения Гаусса. Подобные случаи расчета магнитных схем замещения имеют место тогда, когда работа магнитных материалов происходит на начальном линейном участке кривых намагничивания, где можно считать магнитные проницаемости материалов, а, следовательно, и магнитные сопротивления постоянными величинами. В большом числе случаев, однако, работа магнитных материалов реальных электромагнитных и электромашинных устройств происходит на криволинейных участках кривых намагничивания. Такой выбор режима работы магнитных материалов неслучаен. Можно показать, что при выборе номинального режима работы магнитного материала некоторого устройства на криволинейном участке кривой намагничивания это устройство имеет, как правило, оптимальные массогабаритные характеристики. При работе магнитных материалов на криволинейных участках кривых намагничивания магнитные сопротивления зависят от напряженности и, в конечном итоге, от магнитных потоков схемы. Уравнения в этом случае оказываются нелинейными, что существенно затрудняет их решение. При расчете нелинейных магнитных схем замещения, как правило, отказываются от использования понятий магнитных сопротивлений и применяют так называемые вебер-амперные характеристики ветвей.

Вебер-амперная характеристика (ВАХ) ветви – это зависимость магнитного потока Ф ветви от падения магнитного напряжения U на ветви, т.е. зависимость вида Ф = Ф(U). Вебер-амперную характеристику ветви нетрудно получить, если известны кривая намагничивания магнитного материала ветви, площадь S поперечного сечения ветви и ее длина l, а также, если предположить, что в ветви существует однородное магнитное поле. Действительно, допустим, что известна зависимость . При указанных выше предположениях имеет место: и . Из последних двух равенств после преобразований следует, что

Ф = S B(U/l).

Последнее равенство означает, что для получения ВАХ ветви по кривой намагничивания необходимо умножить ее по оси ординат на величину S, а по оси абсцисс поделить на длину l. Таким образом, приходим к выводу, что ВАХ ветви – это есть кривая намагничивания, представленная в ином масштабе.

Уравнения Кирхгофа при использовании понятия ВАХ ветвей для рассмотренной выше магнитной схемы замещения (см. рис. 5.6, б) принимают вид:

. (5.20)

, (5.21)

, (5.22)

где , , – падения магнитных напряжений соответственно на магнитных сопротивлениях , , . Предполагая, что ВАХ каждой ветви, т.е. зависимости , и , известны, можно решить нелинейную систему уравнений (5.20)–(5.22) относительно неизвестных переменных , и . Магнитные потоки , и нетрудно получить, используя ВАХ и найденные значения падений магнитных напряжений , и .

При расчёте магнитных цепей электромашинных устройств, кроме перечисленных выше понятий, используют также так называемые магнитные характеристики.

Магнитная характеристика электромашинного устройства (электрической машины) – это зависимость магнитного потока Ф, создаваемого обмоткой с током i, от указанного тока i, т.е. зависимость

. (5.23)

Рассмотрим качественный вид магнитных характеристик электромашинных устройств. При этом учтём, что магнитные цепи электромашинных устройств содержат, кроме ферромагнитных участков, также и воздушные зазоры. Рассмотрим также влияние последних на магнитные характеристики электромашинных устройств. Для простоты будем полагать, что магнитная цепь электромашинного устройства представляет собой замкнутый неразветвленный сердечник с небольшим воздушным зазором и одной обмоткой (см. рис. 5.8, а).

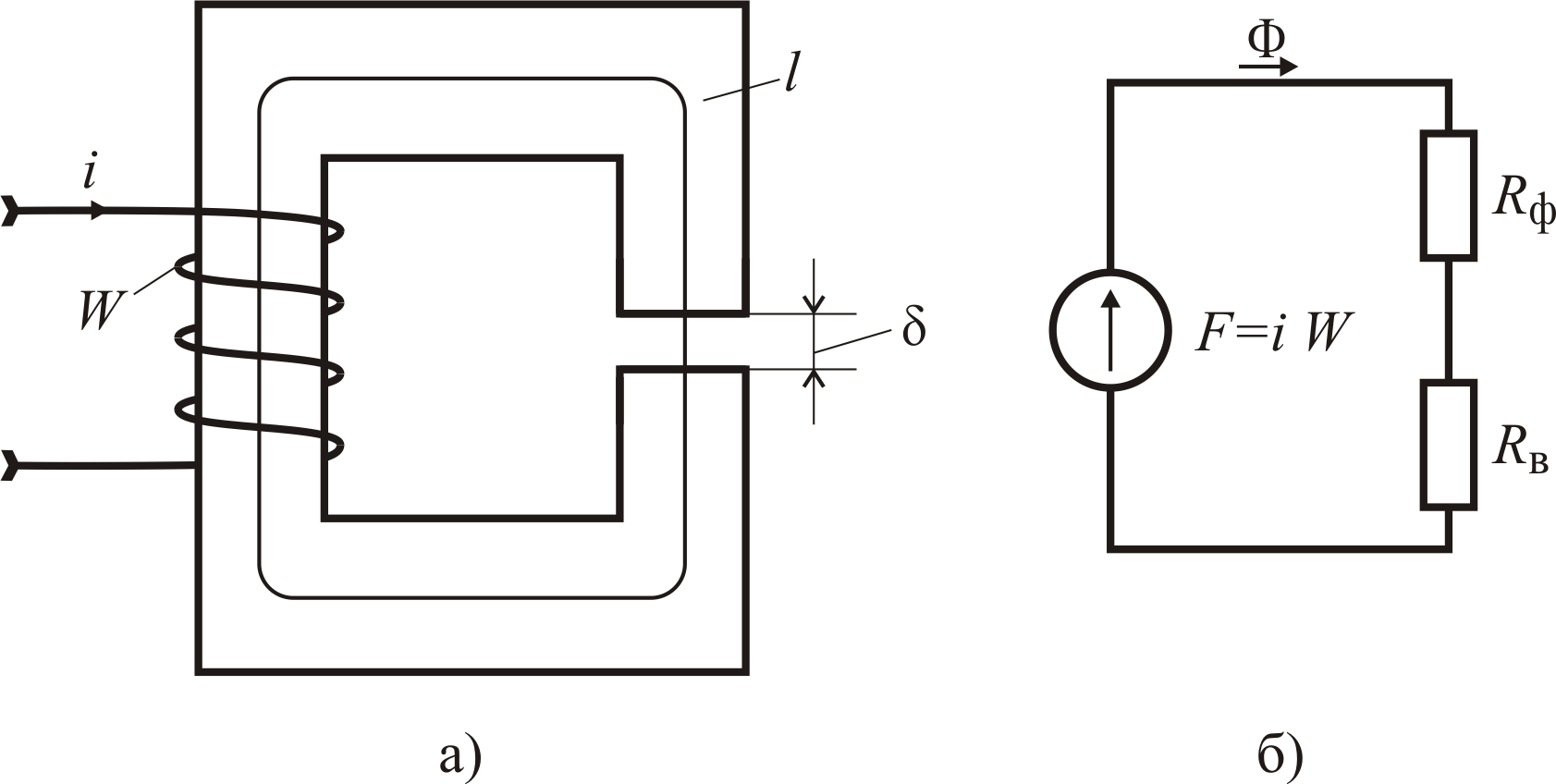
Рис. 5.8. Магнитная цепь с воздушным зазором (а) и её магнитная схема замещения (б)

Будем считать, что обмотка имеет W витков, длина средней линии сердечника равна l, а ширина воздушного зазора – δ. Будем полагать также, что по обмотке W протекает ток i. В этом случае можно считать, что магнитная схема замещения рассматриваемого замкнутого неразветвленного сердечника представляет собой, если пренебречь потоками рассеяния, последовательное соединение МДС обмотки , магнитного сопротивления ферромагнитного участка магнитной цепи и магнитного сопротивления воздушного зазора (см. рис. 5.8, б).

Из магнитной схемы замещения (см. рис. 5.8, б) рассматриваемой магнитной цепи следует уравнение

, (5.24)

составленное по второму закону Кирхгофа. Если положить, что ферромагнитный участок магнитной цепи имеет относительную магнитную проницаемость , а относительная проницаемость воздушного зазора равна единице, то нетрудно получить с учётом (5.9) соотношения для магнитных сопротивлений и :

, (5.25)

, (5.26)

где S – площадь поперечного сечения сердечника.

Заметим, что соотношение (5.26) для магнитного сопротивления воздушного зазора записано в предположении, что площадь поперечного сечения воздушного зазора можно считать равной площади S. В общем случае эти площади имеют различные значения, как показывает более детальный анализ магнитных полей в области воздушных зазоров.

Из (5.24) с учётом (5.25) и (5.26) получим уравнение магнитной характеристики рассматриваемой магнитной цепи

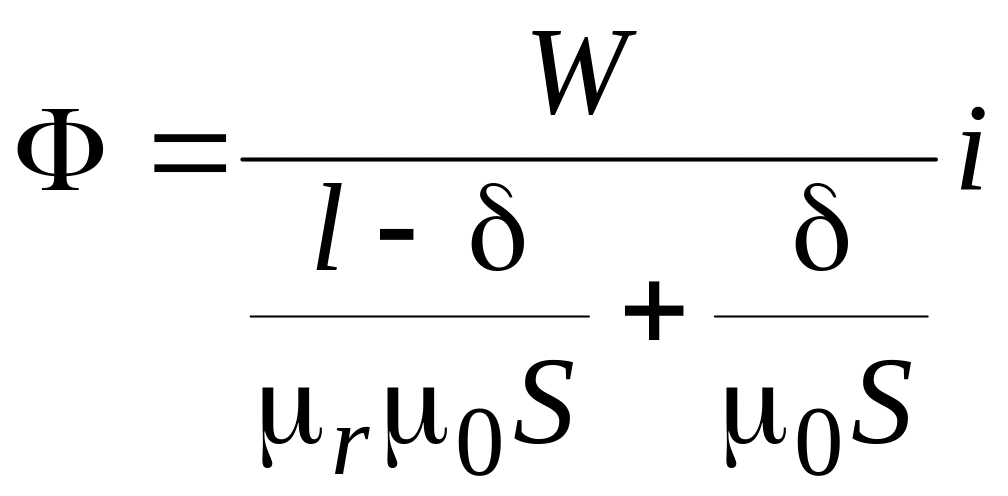. (5.27)

Рассмотрим вначале качественный вид магнитной характеристики (5.27) при , т.е. при условии, что воздушный зазор отсутствует. В этом случае получим, что уравнение магнитной характеристики магнитной цепи без воздушного зазора имеет вид

. (5.28)

Нетрудно показать, что график зависимости , заданной равенством (5.28), можно получить из графика кривой намагничивания материала сердечника путём изменения его масштабов по осям. Действительно, по закону полного тока для рассматриваемой цепи при получим, что

. (5.29)

Тогда из (5.28) и (5.29) следует, что

.

Так как

,

то

.

Последнее равенство с учётом (5.29) можно переписать в виде

. (5.30)

Равенство (5.30) означает, как это известно из аналитической геометрии, что для получения графика необходимо график растянуть по оси абсцисс в раз, а по оси ординат – в S раз. Таким образом, приходим к выводу, что при магнитная характеристика магнитной цепи будет повторять качественно вид кривой намагничивания материала цепи (см. рис. 5.9).

Рис. 5.9. Магнитные характеристики магнитных цепей без воздушного зазора ( ) и с воздушным зазором ( )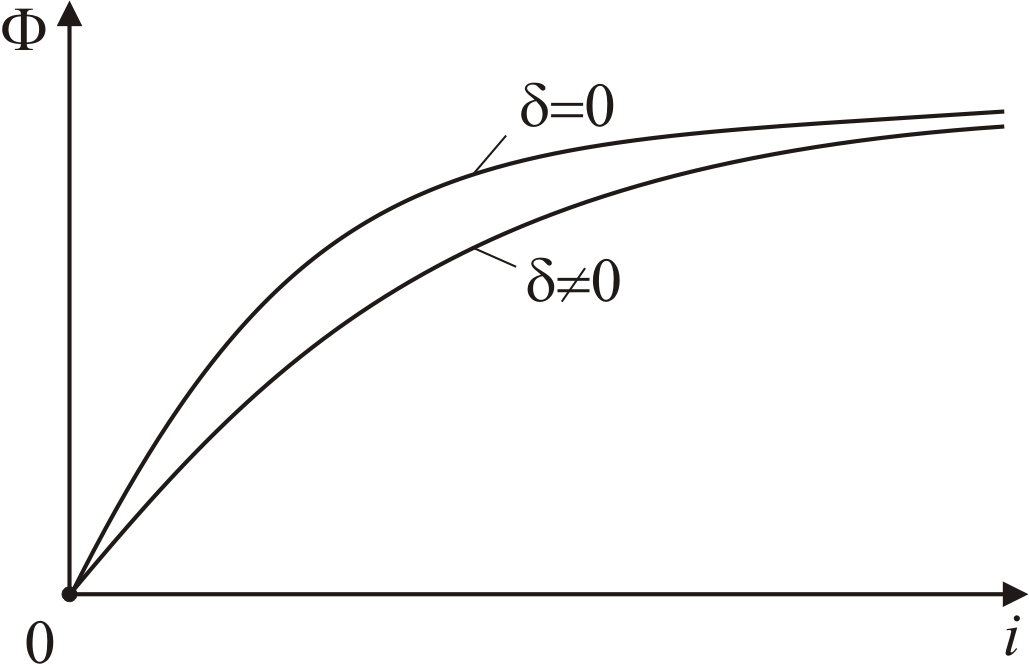

Рассмотрим теперь вид магнитной характеристики при наличии воздушного зазора, т.е. при , опираясь на общее уравнение (5.27) этой характеристики. Для сравнения магнитной характеристики при с магнитной характеристикой при преобразуем (5.27) к виду

, (5.31)

. (5.32)

Из (5.31) и (5.28) видно, что уравнения магнитной характеристики при и при совпадают с точностью до множителя .

При малых значениях тока i напряжённость поля также мала, а значит проницаемость имеет большие значения. Следовательно . Это означает, что для одного и того же тока i магнитный поток Ф при , меньше, чем при . Поэтому магнитная характеристика цепи с воздушным зазором должна располагаться при малых токах i значительно ниже магнитной характеристики цепи без воздушного зазора (см. рис. 5.9).

При больших значениях тока i напряжённость поля велика, а значит и, следовательно, в силу (5.32) . Это означает, очевидно, что при больших токах магнитные характеристики цепи с зазором и без зазора практически совпадают (см. рис. 5.9).

Из сравнения построенных магнитных характеристик видно, что магнитная характеристика с воздушным зазором проходит ниже магнитной характеристики без воздушного зазора и имеет в начальной части существенно меньший наклон, чем магнитная характеристика без зазора. Говорят, что воздушный зазор линеаризует магнитную характеристику магнитной цепи.

Полученные результаты показывают также, что воздушный зазор снижает магнитный поток магнитной цепи. Нетрудно показать, что это снижение является тем большим, чем больше длина воздушного зазора.

Завершая рассмотрение вопроса о магнитных схемах замещения, отметим следующее. Можно показать, опираясь на изложенные выше законы магнитных цепей, что для магнитных схем замещения, составленных для магнитных цепей с постоянными магнитными полями, справедливы перечисляемые ниже свойства:

1. результирующее сопротивление 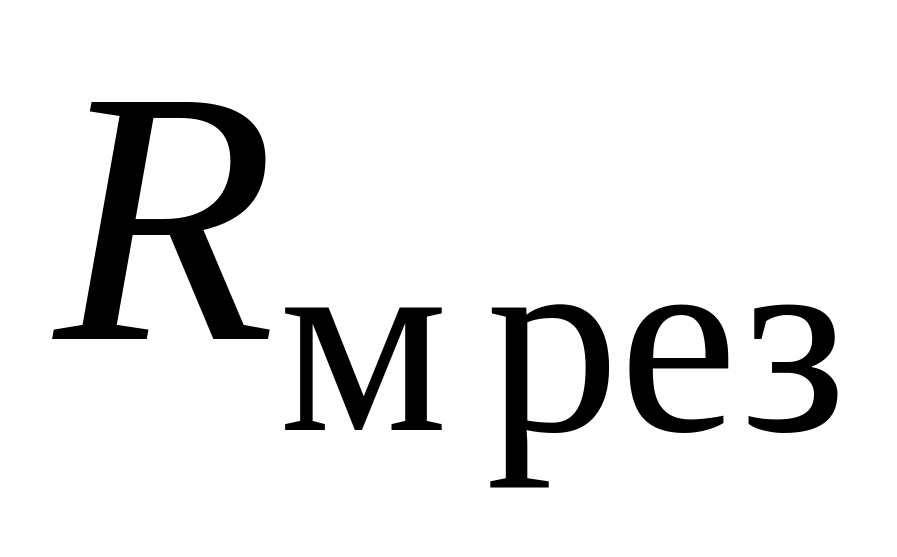последовательного соединения магнитных сопротивлений 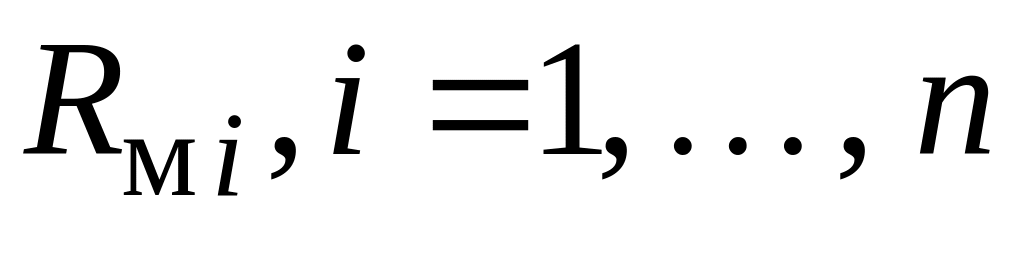, равно их сумме, т.е.

; (5.33)

2. результирующая проводимость параллельного соединения магнитных сопротивлений равна сумме их проводимостей, что можно записать в следующем виде:

; (5.34)

3. при параллельном соединении двух магнитных сопротивлений большая часть магнитного потока ответвляется в магнитное сопротивление с меньшим значением;

4. при последовательном соединении двух сопротивлений большее падение магнитного напряжения устанавливается на магнитном сопротивлении с большим значением.

Можно показать, что аналогичные свойства и соотношения справедливы также и для магнитных цепей с переменными магнитными полями.

Нетрудно заметить, что аналогичными четырьмя свойствами, если их сформулировать в электрических терминах, обладают также и электрические схемы замещения.

При построении теории векторного управления машинами переменного тока возникает необходимость определения индуктивностей и взаимных индуктивностей обмоток указанных машин.

Выведем соотношения для индуктивности обмотки. Будем полагать, что имеется замкнутый сердечник без воздушного зазора с обмоткой, имеющей витков. Также будем полагать, что по обмотке протекает ток (см. рис. 5.10, а).

Согласно (1.26) для определения индуктивности обмотки необходимо определить её собственное потокосцепление , которое обусловлено собственным током . Тогда

. (5.35)

Положив, что поле в сердечнике является однородным, а потоки рассеяния отсутствуют, запишем

, (5.36)

где S – площадь поперечного сечения сердечника; B – магнитная индукция в сердечнике. По закону полного тока запишем

, (5.37)

где l – длина средней линии сердечника. Из (5.35)–(5.37) с учётом (1.16) нетрудно после преобразований получить, что

, (5.38)

где – относительная магнитная проницаемость материала сердечника.

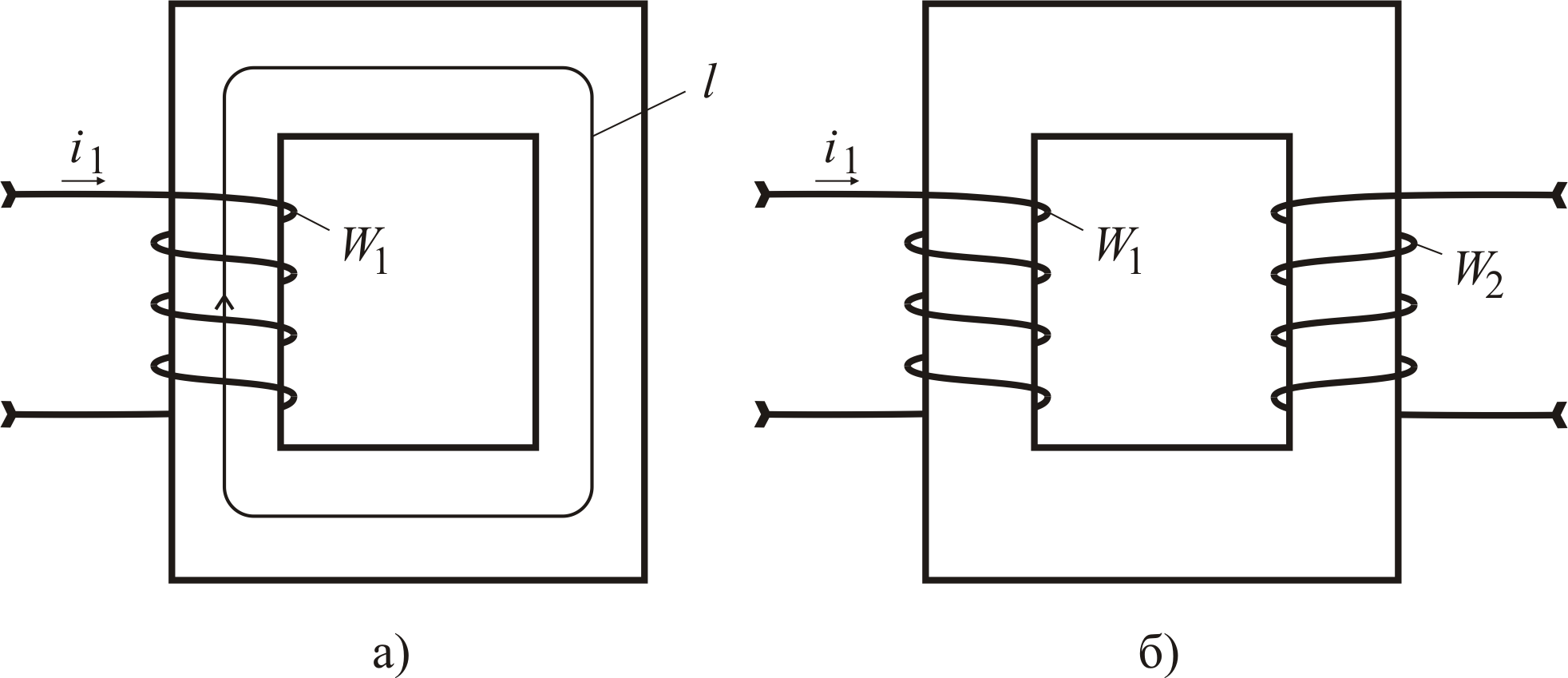
Рис. 5.10. Электромагнитные схема сердечников, поясняющие определение индуктивности (а) и взаимной индуктивности (б) обмоток

На основании (5.38) приходим к следующим выводам.

1. Индуктивность обмотки прямо пропорционально квадрату количества её витков.

2. Коэффициент пропорциональности зависит только от магнитных и конструктивных параметров сердечника.

3. Индуктивность сердечника тем больше, чем больше его магнитная проницаемость и поперечное сечение и чем меньше длина средней линии сердечника.

Определим взаимную индуктивность двух обмоток с количеством витков соответственно и , используя электромагнитную схему, приведённую на рис. 5.10, б.

Предположения о свойствах сердечника здесь примем те же, что и в предыдущей задаче. Согласно (1.27) для определения взаимной индуктивности необходимо определить потокосцепление обмотки , создаваемое током , при условии, что ток обмотки равен нулю. Тогда

. (5.39)

Взаимное потокосцепление

. (5.40)

Так как ток обмотки равен нулю (по условию), то по закону полного тока можно записать

. (5.41)

Из (5.39)–(5.41) с учётом уравнений (1.16) связи величин B и H нетрудно получить после преобразований, что

. (5.42)

На основании (5.42) приходим к следующим выводам.

1. Взаимная индуктивность двух обмоток прямо пропорциональна произведению количества витков этих обмоток.

2. Коэффициент пропорциональности зависит только от магнитных и конструктивных параметров сердечника, на котором установлены обмотки.

3. Взаимная индуктивность обмоток тем больше, чем больше магнитная проницаемость соединяющей их магнитной цепи и ее поперечное сечение и чем меньше длина средней линии этой магнитной цепи.