П а д е н и е м а г н и т н о г о н а п р я ж е н и я обозначается символом и задается соотношением
,
(5.5)
где
a,
b
– начальная
и конечная точки некоторого заданного
контура l,
вдоль которого вычисляется контурный
интеграл;
– соответственно напряженность, длина
участка и угол между направлениями
указанных величин на i-м
участке контура l
(см. рис. 5.3, а).
Нетрудно показать, что для однородного магнитного поля (см. рис. 5.3, б) падение магнитного напряжения между двумя точками, лежащими на одной линии магнитной индукции и находящимися на расстоянии l, определяется из соотношения
.
(5.6)
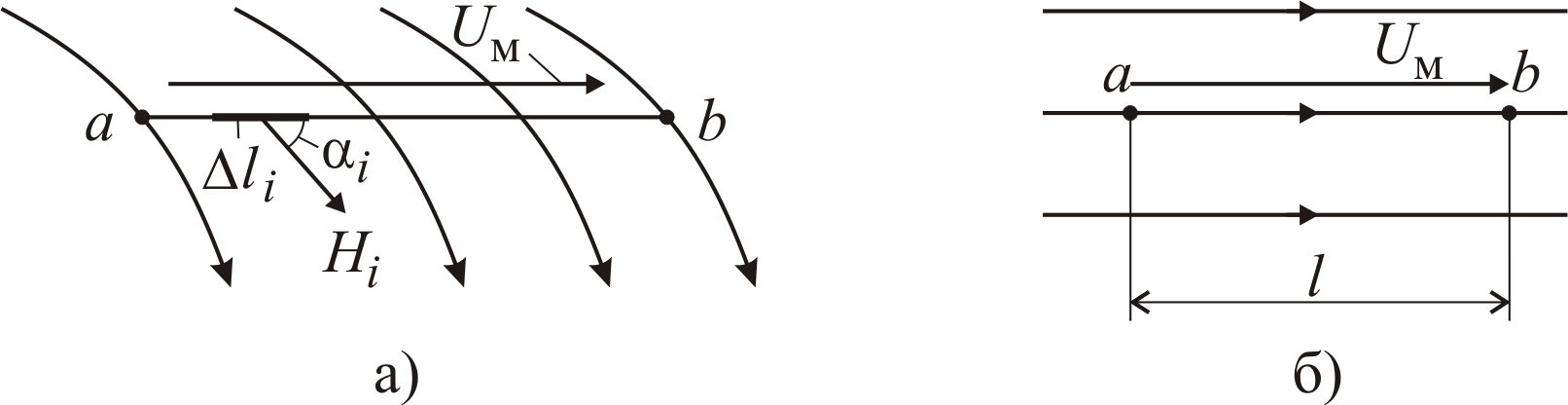
Рис. 5.3. Геометрические пояснения к определению падения магнитного напряжения между точками а и b
Произвольного поля (а) и однородного поля (б)
Для однородных переменных магнитных полей при условии, что напряженность изменяется по синусоидальному закону, падение магнитного напряжения между двумя точками, лежащими на одной линии магнитной индукции и находящимися на расстоянии l, определяется так:
,
(5.7)
где
–
соответственно комплексные падение
магнитного напряжения и напряженность.
Ветвь магнитной цепи – это ее участок, в каждом поперечном сечении которого действует один и тот же магнитный поток.
У з е л магнитной цепи – это область разделения ее на несколько ветвей.
М а г н и т н о е с о п р о т и в л е н и е ветви магнитной цепи обозначается для постоянных магнитных полей символом Rм и задается формулой
,
(5.8)
где – падение магнитного напряжения на ветви; Ф – магнитный поток, действующий в некотором произвольном сечении рассматриваемой ветви.
Магнитное сопротивление Rм ветви, конструкция которой имеет форму прямоугольного параллепипеда (см. рис. 5.4), в том случае, когда в нем существует однородное магнитное поле, можно рассчитать аналитически по формуле
,
(5.9)
где
,
,
– длина, относительная магнитная
проницаемость и площадь поперечного
сечения прямоугольного параллепипеда.
Рис.
5.4. Схема, поясняющая определение
магнитного сопротивления прямоугольного
параллепипеда
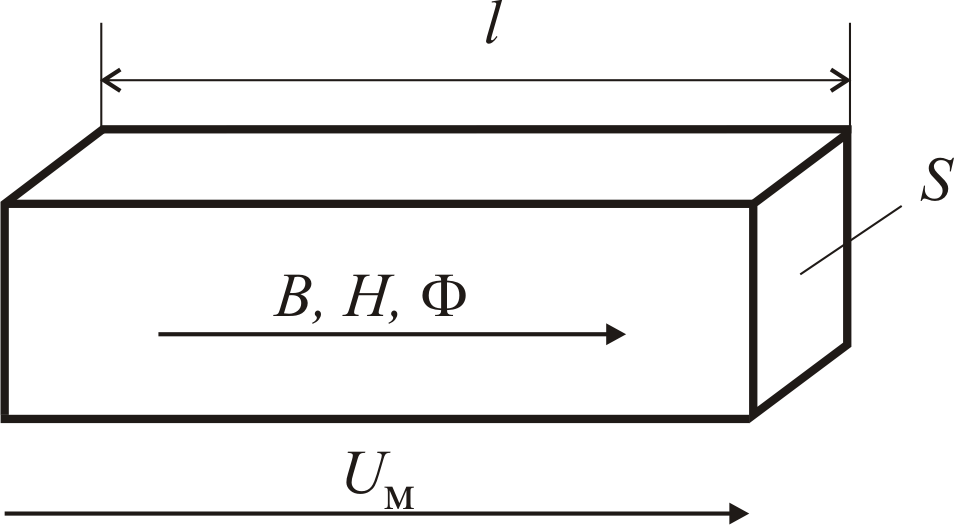
Действительно,
магнитное сопротивление Rм
по определению
задается формулой (5.8). Для однородного
магнитного поля, как это показано выше,
справедливо
и Ф = BS.
Подставив
два последних равенства в (5.8) и учтя,
что B
= μ0 μr
H,
получим после преобразований искомое
соотношение в виде (5.9).
Магнитное
сопротивление зависит от напряженности
Н, т.к. в
соотношение для определения магнитного
сопротивления входит величина
,
зависящая весьма существенно от
напряженности. Если величина
,
рассматриваемая как функция напряженности
Н,
имеет участки убывания и возрастания
(см. рис. 3.9, а), то тогда график зависимости
в силу (5.9) имеет участки соответственно
возрастания и убывания (см. рис. 5.5, а).
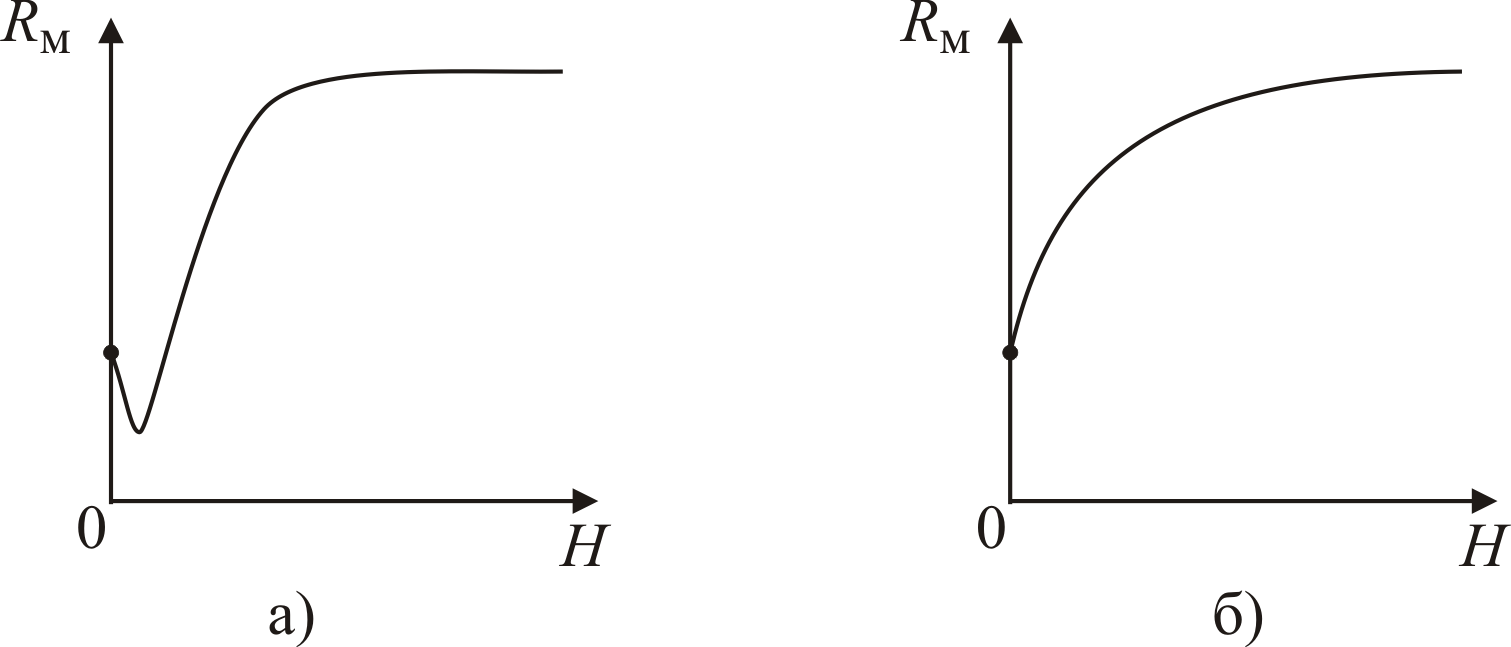
Рис. 5.5. Графики зависимостей магнитных сопротивлений магнитных цепей от напряженностей магнитных полей
Если
величина
монотонно убывает при увеличении
напряженности Н
(см. рис. 3.9, б), то тогда функция
монотонно возрастает (см. рис. 5.5, б).
Следует отметить, что при больших
значениях напряженности магнитное
сопротивление магнитной цепи примерно
в
раз выше, чем при малых значениях, т.е.
при усилении магнитного поля в магнитной
цепи происходит многократное увеличение
ее магнитного сопротивления.
Для
переменных магнитных полей магнитное
сопротивление обозначается комплексной
переменной
и задается формулой
,
(5.10)
где
– соответственно активное и реактивное
сопротивления магнитной цепи.
Напомним, что знак подчеркивания в переменной означает комплексный характер такой переменной. В ряде случаев, когда необходимо уменьшить громоздкость обозначений или комплексный характер переменных ясен из контекста, знак подчеркивания может быть опущен.
Можно
показать, что величина
,
если площадь петли гистерезиса равна
нулю, иначе
и тем больше, чем больше площадь петли
гистерезиса.
М а г н и т н а я п р о в о д и м о с т ь ветви магнитной цепи обозначается символом Gм и задается в зависимости от типа магнитного поля следующими формулами:
,
,
(5.11)
где
,
– магнитные проводимости ветвей
соответственно для постоянного и
переменного магнитных полей.
М а г н и т н а я с х е м а з а м е щ е н и я м а г н и т н о й ц е п и – это ее условное графическое изображение в виде соединений по определенным правилам совокупности МДС и магнитных сопротивлений, соответствующих отдельным ветвям этих цепей.
Магнитные схемы замещения вводятся с целью проведения анализа свойств магнитных цепей и упрощения их расчета. Составление магнитных схем замещения основывается на следующих правилах:
1) выделяются участки магнитной цепи, где магнитные потоки можно считать постоянными величинами, т.е. выделяются ветви магнитной цепи;
2) ветвь магнитной цепи без обмотки представляется магнитным сопротивлением; при этом считается, что между выводами магнитного сопротивления существует некоторое падение магнитного напряжения, а по магнитному сопротивлению протекает некоторый магнитный поток;
3) ветвь магнитной цепи с обмоткой представляется последовательным соединением МДС данной обмотки и магнитного сопротивления этой ветви; при этом считается, что через МДС и по магнитному сопротивлению протекает некоторый магнитный поток;
4) каждая область магнитных цепей, где сходятся три и более магнитных потоков, замещается узлом;
5) соединение только двух ветвей, каждая из которых соединяется с другой ветвью только одним выводом, представляется последовательным соединением соответствующих им магнитных сопротивлений.
Остальные особенности построения магнитных схем замещения будут ясны после рассмотрения следующих примеров. Рассмотрим вначале пример построения магнитной схемы замещения для магнитной цепи, изображенной на рис. 5.6, а.
При этом будем полагать, что линии магнитной индукции не ответвляются в воздух, т.е. не ответвляется в воздух и магнитный поток. Тогда магнитная схема замещения рассматриваемой магнитной цепи (рис. 5.6, а), составленная с учетом записанных выше правил, примет вид, представленный на рис. 5.6, б.
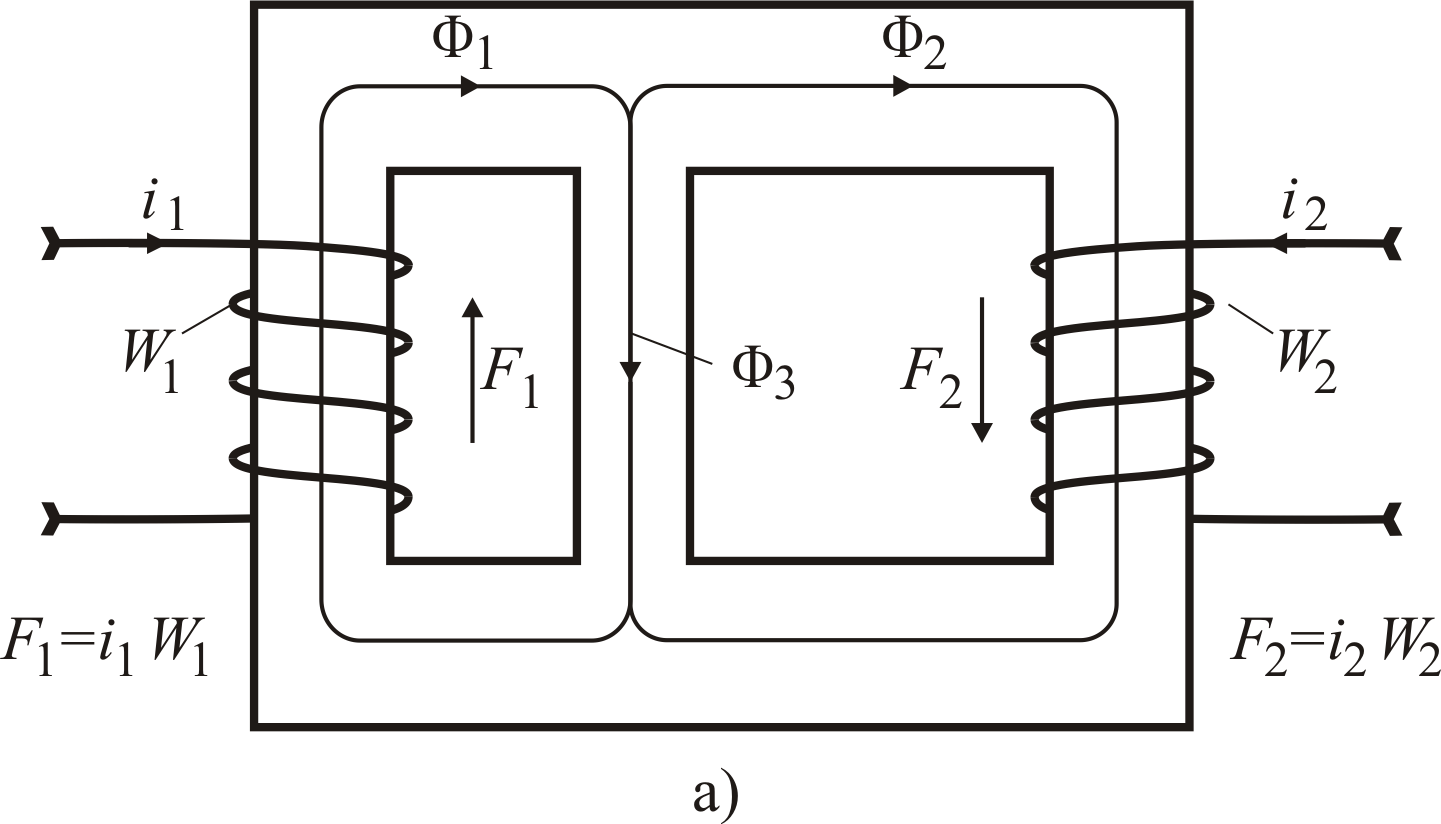
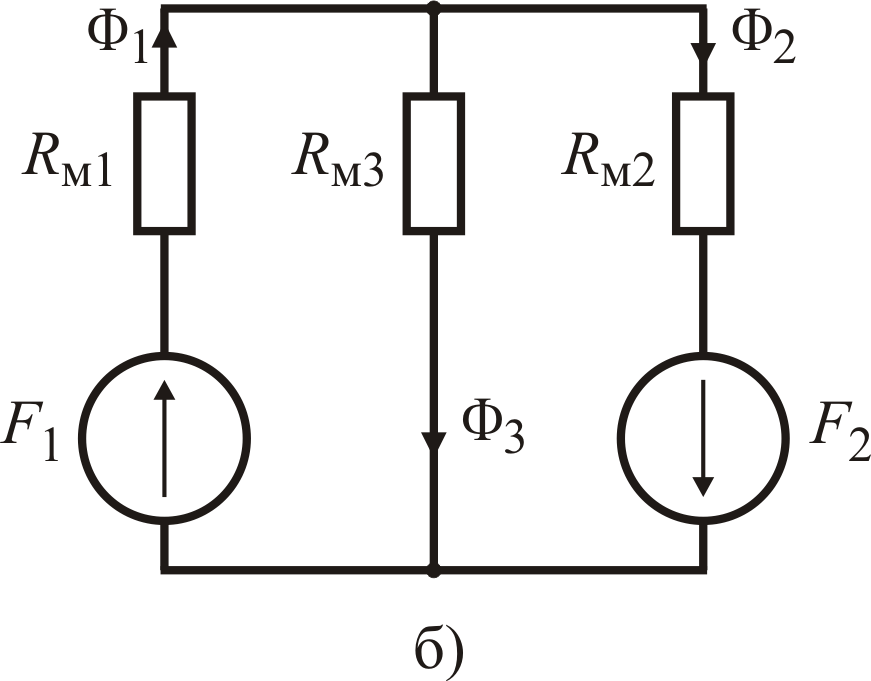
Рис. 5.6. Электромагнитная схема магнитной цепи (а)