5. Основные понятия электромагнитного расчета электромашинных устройств

При проектировании электромашинных устройств используют три основных метода для их электромагнитного расчета [16, с. 10].

Первый метод основан на использовании закона полного тока (1.12), принципа непрерывности магнитного потока, закона электромагнитной индукции (1.23), законов преломления линий магнитной индукции на границе раздела двух сред и соотношения (1.13), связывающего векторы магнитной индукции, напряженности и намагниченности [2, с. 89].

П р и н ц и п н е п р е р ы в н о с т и м а г н и т н о г о п о т о к а в словесной формулировке записывается так: магнитный поток, пронизывающий любую замкнутую поверхность, равен нулю. Математически принцип непрерывности магнитного потока представляется следующим соотношением:

, (5.1)

где S – некоторая замкнутая поверхность; – вектор магнитной индукции в той точке поверхности S, в которой находится элемент ; – скалярное произведение векторов и ;  – угол между векторами и .

При проектировании электромашинных устройств практический интерес представляют з а к о н ы п р е л о м л е н и я л и н и й м а г н и т- н о й и н д у к ц и и на границе раздела ферромагнетиков и воздуха. Для этого случая данные законы в упрощенной формулировке записываются так: 1) линии магнитной индукции выходят из ферромагнетика в воздух по нормали к поверхности ферромагнетика, исключая случай, указанный в пункте 2; 2) если линия магнитной индукции проходит в ферромагнетике параллельно плоскости, касательной к поверхности ферромагнетика, то она не выходит в воздух; при этом, однако, в воздухе, вблизи поверхности ферромагнетика также существует магнитное поле, линии которого также параллельны плоскости, касательной к поверхности ферромагнетика (см. рис. 5.1); в этом случае магнитные индукции ферромагнетика и воздуха связаны соотношением

, (5.2)

где – относительные магнитные проницаемости соответственно ферромагнетика и воздуха.

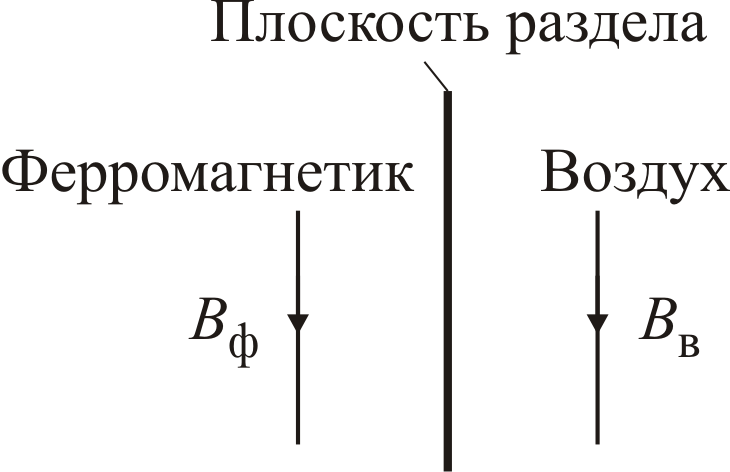
Рис. 5.1. Взаимное расположение линий магнитной индукции в ферромагнетике и в воздухе при их прохождении в ферромагнетике параллельно поверхности

ферромагнетика

Соотношение (5.2) означает физически, что при параллельном расположении линий магнитной индукции вблизи поверхности раздела "ферромагнетик-воздух" магнитная индукция в воздухе меньше, чем в ферромагнетике, в раз, т.е. поле в воздухе относительно слабое. Тем не менее, как показывает практика проектирования и эксплуатации электромагнитных устройств, такое поле в воздухе необходимо в ряде случаев учитывать.

В более строгой формулировке на границе раздела двух сред выполняется, как это показано в теории электромагнетизма, следующее условие: при переходе из одной среды в другую сохраняются нормальная составляющая магнитной индукции и тангенциальная составляющая напряженности.

Заключая изложение первого метода, заметим, что он не выдвигает каких-либо существенных упрощающих допущений в отношении свойств магнитных полей и картин линий магнитной индукции в электромашинных устройствах, что приводит к трудоемким, громоздким вычислениям, но обеспечивает в конечном итоге низкую погрешность расчета значений магнитных величин.

Второй метод рассматривает электромашинные устройства как магнитные цепи (понятие о магнитных цепях дается ниже) и для расчета последних использует так называемые первый и второй законы Кирхгофа для магнитных цепей. Представление об электромашинных устройствах как о магнитных цепях возможно, как правило, только при заметных (но вполне допустимых для инженерной практики) упрощающих допущениях относительно свойств магнитных полей. Указанный метод упрощает проведение расчетов и повышает их наглядность, но увеличивает погрешность вычисления магнитных величин. Заметим, забегая вперед, что первый закон Кирхгофа вытекает из принципа непрерывности магнитного потока, а второй закон Кирхгофа – из закона полного тока.

Третий метод представляет комбинацию первых двух. Считается, что третий метод является наиболее эффективным. Его использование предполагает, в частности, рассмотрение конструкций электромашинных устройств как магнитных цепей и расчет последних с использованием понятий магнитных цепей. Перейдем к рассмотрению этих понятий.

М а г н и т н а я ц е п ь – это совокупность устройств, содержащих ферромагнитные и иные тела, электромагнитные процессы в которых могут быть описаны с использованием понятий магнитодвижущей силы, магнитного потока и падения магнитного напряжения. Из приведенного определения следует, что необходимо рассмотрение понятий магнитодвижущей силы и падения магнитного напряжения.

М а г н и т о д в и ж у щ а я с и л а (МДС) – это вектор , имеющий модуль

F = i W , (5.3)

где i – ток катушки; W – число витков катушки, и направленный по продольной магнитной оси магнитного поля катушки так, что его положительное направление связано с направлением тока i правилом правого винта (см. рис. 5.2).

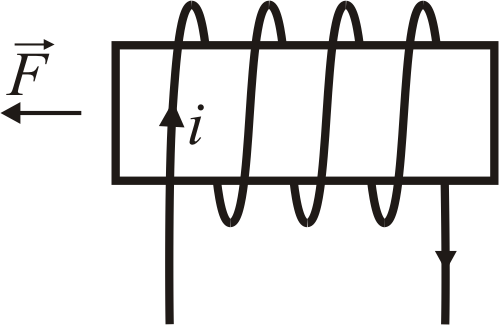
Рис. 5.2. Схема, поясняющая правило определения положительного направления МДС

Для переменных магнитных полей в случае изменения тока по синусоидальному закону соотношение для МДС записывается так:

, (5.4)

где – соответственно комплексные МДС и ток.

МДС называют также н а м а г н и ч и в а ю щ е й с и л о й (НС).