6. Основные понятия теории электрических цепей

Теория электромашинных устройств, кроме рассмотренных выше понятий магнитных цепей, широко использует также ряд понятий электрических цепей. В данном разделе напомним наиболее сложные из них. К таким понятиям относятся, прежде всего, определения электрических величин, описывающих электрические цепи переменного тока. Эти определения основываются на свойствах комплексных чисел. Комплексные числа используются также при рассмотрении теории векторного управления машинами переменного тока и при решении линейных дифференциальных и операторных уравнений, описывающих электромашинные устройства. Для студентов, изучающих теорию электромашинных устройств, крайне важна техника работы с комплексными числами. Здесь нужно, во-первых, помнить основные операции над комплексными числами. Во-вторых, необходимо чётко представлять геометрический смысл комплексного числа и, в-третьих, знать три формы записи комплексного числа: алгебраическую, тригонометрическую и показательную. Напомним основные сведения по перечисленным вопросам.

Понятие числа прошло длительную историю развития [17, с. 180, 181]. Первоначально на практике использовались только натуральные числа: 1, 2, 3 и т.д. Такие числа всегда позволяют выполнять операцию сложения, но не всегда операцию вычитания. Для реализации во всех случаях операции вычитания были введены целые отрицательные числа и нуль.

Целые положительные и отрицательные числа всегда позволяют выполнять операцию умножения. Но операция деления не всегда выполнима. Для реализации ее во всех случаях потребовалось введение обыкновенных дробей, т.е. чисел, равных отношению целых чисел (положительных и отрицательных).

Целые числа и обыкновенные дроби сформировали совокупность чисел, которые назвали рациональными числами. Любое рациональное число можно возвести в целую степень, также получив рациональное число. Но обратная операция – операция извлечения корней – не всегда выполнима на множестве рациональных чисел. Так, например, показано, что число не представляется ни целым числом, ни обыкновенной дробью, то есть не является рациональным числом. Это обстоятельство потребовало введения так называемых иррациональных чисел.

Рациональные и иррациональные числа образуют так называемое множество действительных чисел. Замечательным в отношении действительных чисел является тот факт, что если, как это показано в математике, каждому действительному числу сопоставить некоторую точку на числовой оси, то такая совокупность точек составит непрерывную линию.

С дальнейшим развитием математики и ее приложений возникла следующая проблема. Любое действительное число можно возвести в квадрат, получив также действительное число. Выполнить же обратную операцию – извлечение квадратного корня – не всегда возможно: невозможно, например, извлечь квадратный корень из отрицательного числа, если использовать только понятие действительных чисел. Необходимость же такой операции возникает, например, при решении уравнения

, (6.1)

которое формально можно решить так. Перепишем это уравнение в виде

(6.2)

Откуда следует, что формально решение можно записать следующим образом:

(6.3)

Вспоминая, однако, что квадрат любого действительного числа есть величина положительная, приходим к выводу о том, равенство (6.2) для действительных чисел не может выполняться, т.к. его левая часть всегда положительная или ноль, а правая является отрицательной. Таким образом, возникает противоречие. Следовательно, число х, задаваемое равенством (6.3), не может быть действительным числом, а операция извлечения квадратного корня из отрицательного числа невыполнима на множестве действительных чисел.

Из изложенного также следует, что уравнение (6.1) на множестве действительных чисел не имеет решения. Если все-таки потребовать, чтобы уравнение (6.1) имело решение, то нужно признать, что величина есть число какого-то нового типа. Этот тип чисел называют комплексными числами.

Подобная ситуация возникает и в других случаях решения квадратных уравнений. Действительно, для квадратного уравнения общего вида

(6.4)

решение, как известно, представляется так:

(6.5)

Введем следующее обозначение для второго слагаемого в равенстве (6.5):

. (6.6)

Тогда равенство (6.5) можно записать так:

. (6.7)

Если

, (6.8)

то число из (6.6) и (6.7) не может быть действительным, так как при возведении в квадрат обеих частей равенства (6.6) приходим к противоречию: положительная левая часть равна отрицательной правой.

Если потребовать, чтобы уравнение (6.4) всегда имело решение, то необходимо признать, что величина является числом нового типа. Это число, как и число , называют комплексным.

Заметим далее, что число имеет специальное название: оно именуется мнимой единицей и обозначается буквой i, а в электротехнике буквой j. Итак, имеем, что

. (6.9)

Преобразуем далее (6.6) формально так:

(6.10)

С учетом (6.9) получим из (6.10), что

(6.11)

Заметим, что в (6.11) подкоренное выражение в силу условия (6.8) является положительным. Значит, квадратный корень может быть вычислен с использованием понятия действительных чисел и представляет собой некоторое действительное число.

Введем обозначения

, . (6.12)

Тогда после преобразований равенства (6.7) с учетом обозначений (6.11) и (6.12) получим

(6.13)

Говорят, что соотношение (6.13) задает комплексное число в алгебраической форме. Здесь a, b – действительные числа; i – мнимая единица.

Говорят так же, что величина a – это реальная (действительная) часть, а величина b – это мнимая часть комплексного числа z. При этом для реальной и мнимой частей вводят соответственно обозначения Re z и Im z.

Итак,

Re z = a, Im z = b, (6.14)

Для того, чтобы отличать комплексные числа от других чисел, принято эти числа обозначать со знаком подчёркивания. Однако в данном разделе, чтобы упростить записи и сделать их менее громоздкими, знак подчёркивания опущен, когда ясно, что речь идет о комплексных числах.

Можно показать, что для комплексных чисел допустимы все алгебраические операции, если принять следующие правила:

1. два числа и 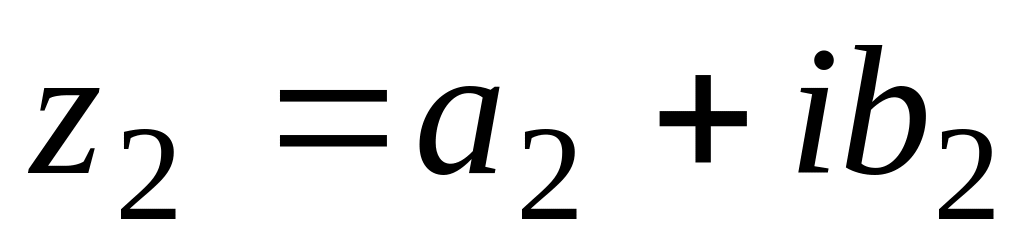равны тогда и только тогда, когда

, ; (6.15)

2. суммой чисел и называется число

; (6.16)

3. произведением чисел и называется число z, получаемое при перемножении и по обычным правилам алгебры и замене произведения на действительное число –1, что иллюстрируется следующими преобразованиями [18, с. 11]:

(6.17)

Заметим, что введение комплексных чисел позволило решить ряд важных задач, например, позволило доказать, что полином n-ой степени имеет n корней. Кроме того, позволило выполнять операцию взятия логарифмов отрицательных чисел, а также решать, например, уравнения вида

,

где k – любое число [17, c. 181].

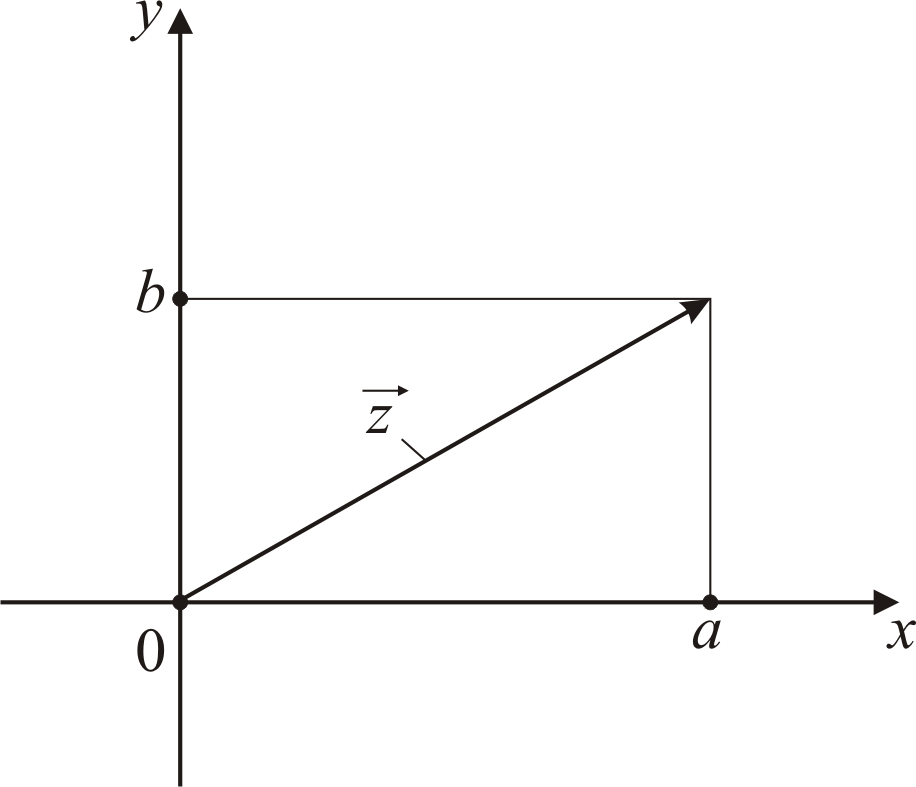
Рассмотрим геометрический смысл комплексного числа. Пусть имеется прямоугольная система координат (x, y) и комплексное число По оси абсцисс будем откладывать действительную часть a комплексного числа z, а по оси ординат – мнимую часть b. Тогда вектор (см. рис.6.1), основание которого лежит в начале координат, а вершина в точке с координатами (a, b), представляет собой геометрический образ комплексного числа z. Нетрудно видеть, что операция сложения (6.16) означает геометрически, что комплексные числа складываются так же, как и векторы, т.е. по правилу параллелограмма.

Рис. 6.1. Схема, поясняющая геометрический смысл комплексного числа в тригонометрической форме

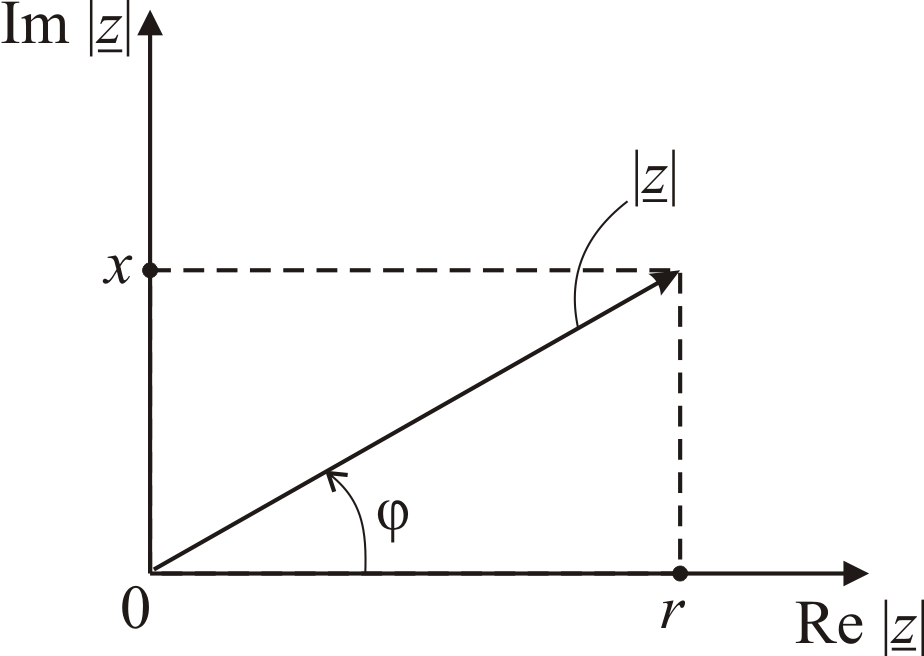
Рассмотрим геометрический смысл операции умножения, заданной равенствами (6.17).

Для этого введём так называемую тригонометрическую форму комплексного числа (см. рис. 6.2). Здесь r – длина вектора , именуемая модулем комплексного числа z; – угол между осью x и вектором , именуемый аргументом комплексного числа z.

Величины r и имеют также и другие обозначения: модуль числа z обозначают , а аргумент – символом arg z. Итак, arg z.

Рис. 6.2. Схема, поясняющая геометрический смысл комплексного числа в тригонометрической форме

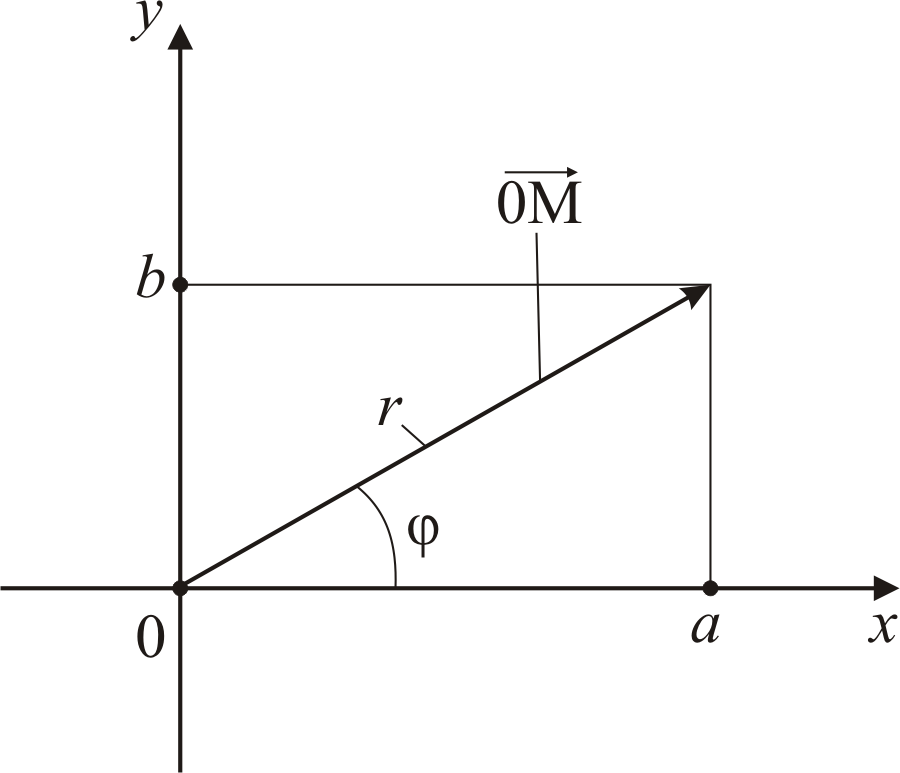
Из рис. 6.2 следует, что

, . (6.18)

Из (6.13) и (6.18) следует

(6.19)

Говорят, что (6.19) задаёт комплексное число в тригонометрической форме.

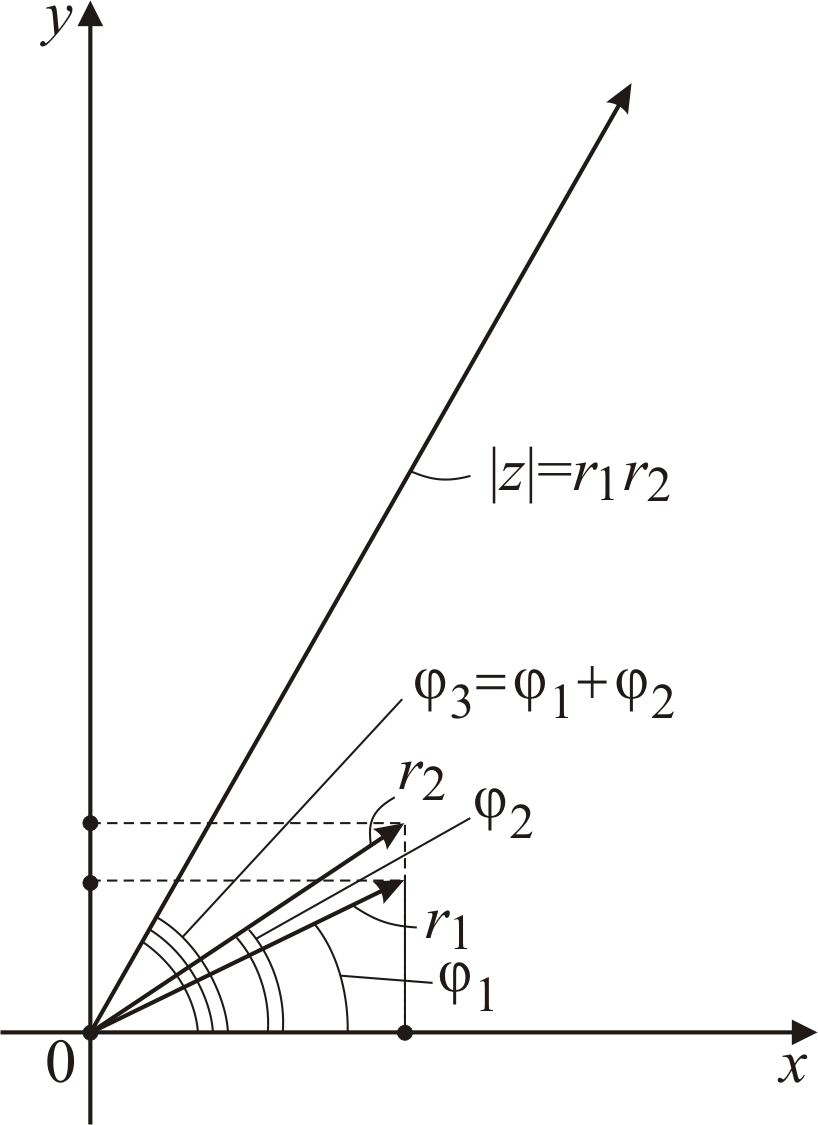
Перейдем теперь непосредственно к рассмотрению геометрического смысла операции умножения. Пусть имеется два числа, заданных в тригонометрической форме:

, (6.20)

. (6.21)

Определим произведение , опираясь на правило (6.17). Тогда после преобразований получим

(6.22)

Учитывая, что первое и второе слагаемые в квадратных скобках представляют собой косинус суммы углов φ₁ и φ₂, а третье и четвертое слагаемые – синус суммы тех же углов, то из (6.22) получим

(6.23)

Из (6.23) нетрудно видеть, что для получения произведения двух комплексных чисел необходимо просуммировать их аргументы, а модули перемножить. Геометрически это означает, что вначале необходимо вектор повернуть на угол (против часовой стрелки), а затем растянуть его длину в раз (см. рис. 6.3).

Рис. 6.3. Схема, поясняющая геометрический смысл операции умножения двух комплексных чисел

Опираясь на правило перемножения комплексных чисел в тригонометрической форме, нетрудно получить соотношение для возведения комплексного числа в n-ю степень. Действительно, пусть n =2. Тогда в силу (6.23) при имеем

(6.24)

При n =3 получим

(6.25)

Применив метод математической индукции, можно получить искомое соотношение для возведения комплексного числа в n-ю степень в следующем виде:

(6.26)

Остановимся далее на технике деления комплексных чисел, представленных в алгебраической форме.

Введем вначале следующее понятие. Число

(6.27)

называют комплексно сопряженным для числа

Пусть требуется определить частное z от деления двух чисел и , что можно записать так:

(6.28)

Умножим числитель и знаменатель соотношения (6.28) на число , которое является комплексно сопряженным для числа , и выполним затем следующие преобразования:

(6.29)

Эти преобразования и задают порядок действий при делении двух комплексных чисел, результатом которого является комплексное число, представленное в алгебраической форме.

Для комплексных чисел, заданных в тригонометрической форме нетрудно показать, учитывая (6.29) и (6.19), что справедливо

. (6.30)

Соотношение (6.30) показывает, что для получения частного от деления комплексного числа на число необходимо повернуть вектор по часовой стрелке на угол и отложить на полученном направлении вектор (иначе говоря, сжать длину вектора в раз).

Кроме двух рассмотренных выше форм представления комплексных чисел существует ещё третья форма – показательная. В теории комплексных чисел доказана так называемая формула Эйлера

(6.31)

Опираясь на формулу Эйлера (6.31), можно некоторое комплексное число

(6.32)

записать в виде

(6.33)

Соотношение (6.33) задаёт комплексное число в показательной форме.

Показательная форма удобна в случае выполнения операций умножения, деления и возведения в степень. Нетрудно показать, учитывая формулы (6.23), (6.26) и (6.30), что для двух комплексных чисел

, (6.34)

справедливо

(6.35)

(6.36)

Опираясь на (6.35) и (6.36) нетрудно показать, что модуль произведения двух комплексных чисел равен произведению модулей этих чисел, а модуль отношения двух комплексных чисел равен отношению модулей этих чисел. Математически эти утверждения могут быть записаны в следующем виде:

. (6.37)

Нетрудно также показать, что модуль произведения нескольких комплексных чисел равен произведению модулей этих чисел.

В случае, если комплексное число задано в алгебраической форме, т.е. z = a + jb, то его модуль и аргумент φ определяются, как это нетрудно видеть из рис. 6.2 с учетом (6.14), по формулам

. (6.38)

Остановимся далее на некоторых функциях комплексного переменного.

В теории функций комплексного переменного вводят, например, показательную функцию, которая используется в операционном исчислении, применяемом для исследования элементов и систем автоматического управления, в том числе, для анализа электромашинных устройств.

Пусть имеется комплексная переменная . Показательной называют функцию f(z) вида [18, с. 32; 19, с. 298]

Приведём к сведению соотношения для некоторых тригонометрических функций, а также для логарифмической, общей степенной и общей показательной функций [18, с. 35, 36, 42, 43].

Пусть имеется комплексная переменная . Тригонометрические функции комплексного аргумента z задаются по определению следующим образом:

.

Можно показать, что при таком определении тригонометрических функций комплексного аргумента для них справедливы все формулы тригонометрических функций действительного аргумента. Например, справедливы соотношения:

,

и т.п.

Пусть – комплексная переменная. Логарифмическая функция обозначается символом Ln(z) и задаётся соотношением

, . (6.39)

Пусть – произвольное комплексное число и – комплексная переменная. Общая степенная функция обозначается символом и задаётся соотношением

, . (6.40)

Пусть – произвольное комплексное число и – комплексная переменная.

Общая показательная функция обозначается символом и задаётся соотношением

(6.41)

В заключение заметим, что введение комплексных чисел является последним расширением числовой системы [17, с. 181]. Располагая комплексными числами, можно выполнить любые известные алгебраические операции, в частности, извлекать корни из отрицательных чисел, находить логарифмы отрицательных чисел, решать, например, уравнение , где а – любое комплексное число.

Таким образом, любые алгебраические действия над комплексными числами выполнимы, причем в результате этих действий опять получаются комплексные числа, а поэтому введение каких-то новых чисел для реализации алгебраических операций больше не требуется.

Рассмотрим далее основные понятия электрических цепей переменного тока, которые необходимо знать при изучении электромашинных устройств.

Электрическая цепь – совокупность объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об ЭДС, токе и напряжении [1, с. 11].

Пусть напряжение изменяется по закону гармонических колебаний (или по синусоидальному закону), т.е.

, (6.42)

где – амплитуда напряжения; – угловая частота изменения напряжения; – начальная фаза напряжения. Тогда, как известно из курса теоретических основ электротехники, при расчете цепей переменного тока может быть использован символический метод, основанный на применении следующих комплексных величин, соответствующих напряжению .

Величина

(6.43)

называется комплексной амплитудой напряжения [2, с. 187].

Величина

(6.44)

называется комплексным напряжением, соответствующим мгновенному напряжению из (6.42) [2, с. 187].

Величина

(6.45)

называется действующим напряжением, соответствующим мгновенному напряжению из (6.42).

Аналогичные понятия вводятся и для токов, изменяющихся по синусоидальному закону

, (6.46)

где – амплитуда тока; – угловая частота изменения тока; – начальная фаза тока.

Величина, равная отношению комплексного напряжения, действующего на некотором элементе электрической цепи, к комплексному току, протекающему по этому элементу, называется комплексным сопротивлением данного элемента электрической цепи [2, с. 191].

Комплексное сопротивление обозначается символом и вычисляется (согласно его определения) по формуле

, (6.47)

где – комплексный ток, соответствующий мгновенному току i из соотношения (6.46). Нетрудно видеть, что комплексное сопротивление является комплексным числом.

Напомним физический смысл комплексного сопротивления . Для этого преобразуем равенство (6.47) с учетом показательной формы числа , а также соотношений для комплексного напряжения и комплексного тока к виду

, (6.48)

где – соответственно модуль и аргумент числа . Из последнего соотношения видно, что

, (6.49)

. (6.50)

Соотношения (6.49) и (6.50) указывают, таким образом, следующий физический смысл комплексного сопротивления .

Во-первых, модуль комплексного сопротивления некоторого элемента электрической цепи равен отношению амплитуды напряжения, действующего на этом элементе, к амплитуде тока, протекающего по данному элементу. Во-вторых, аргумент комплексного сопротивления равен разности начальных фаз указанных напряжения и тока или, как говорят, сдвигу по фазе между указанными напряжением и током.

Из соотношения (6.47) с учётом (6.45) следует также, что

, (6.51)

где I – действующий ток.

Поэтому можно считать, что модуль комплексного сопротивления некоторого элемента электрической цепи равен отношению действующего напряжения к действующему току, соответствующими данному элементу.

Модуль комплексного сопротивления элемента электрической цепи называется полным сопротивлением этого элемента. Поэтому изложенные выводы в отношении модуля комплексного сопротивления справедливы и в отношении полного сопротивления.

Реальная часть комплексного сопротивления элемента электрической цепи называется активным сопротивлением этого элемента и обозначается символами r или R. Математически это определение, например, величины r записывается так:

. (6.52)

Мнимая часть комплексного сопротивления элемента электрической цепи называется р е активным сопротивлением этого элемента и обозначается символами x или X. Математически это определение, например, величины x записывается так:

. (6.53)

С учетом введенных понятий активного и реактивного сопротивлений можно записать комплексное сопротивление элемента электрической цепи в следующей алгебраической форме:

. (6.54)

Соотношение (6.54) позволяет указать геометрический смысл величин , , (см. рис. 6.4), задающих комплексное сопротивление .

Исходя из геометрического смысла комплексного сопротивления или опираясь на соотношения (6.38), (6.52) и (6.53), нетрудно получить формулу для определения полного сопротивления элемента электрической цепи по его активному и реактивному сопротивлениям в следующем виде:

. (6.55)

Через величины r и x можно также определить аргумент  комплексного сопротивления . Из геометрических соображений (см. рис. 6.4) ясно, что

. (6.56)

Аргумент комплексного сопротивления , как отмечалось выше, равен сдвигу по фазе между напряжением, которое действует на этом сопротивлении, и током, который протекает по данному сопротивлению.

Рис. 6.4. Схема, поясняющая геометрический смысл комплексного сопротивления

Таким образом, приходим к следующим выводам, которые справедливы в случае, если для электрической цепи известны ее электрическая схема замещения и значения параметров последней.

1. Для определения полного сопротивления некоторого участка электрической цепи необходимо вычислить комплексное сопротивление этого участка цепи в алгебраической форме , а затем найти его модуль по формуле (6.55).

2. Для определения сдвига по фазе  между током и напряжением, действующими на некотором участке электрической цепи, необходимо вычислить комплексное сопротивление этого участка цепи в алгебраической форме , а затем по формуле (6.56) вычислить искомый сдвиг по фазе .

Рассмотрим пример определения полного сопротивления и сдвига по фазе  между током и напряжением для электрической схемы замещения, представляющей собой параллельное соединение активного сопротивления R и индуктивности L. При этом будем полагать, что токи и напряжения данной схемы изменяются по гармоническому (синусоидальному) закону с круговой частотой ω.

Вначале следует определить комплексное сопротивление этой схемы замещения. Его можно найти, опираясь на общую формулу результирующего сопротивления параллельного соединения элементов электрической схемы замещения. Для двух элементов эта формула имеет следующий вид:

, (6.57)

где – комплексные сопротивления соответственно первого и второго элементов рассматриваемой схемы замещения. В данном примере . Подставив эти величины в (6.57), после преобразований получим

. (6.58)

Полное сопротивление есть модуль комплексного сопротивления . Модуль нетрудно найти, опираясь на рассмотренные выше общие правила преобразования комплексных чисел. Следуя этим правилам можно записать, что

. (6.59)

Для определения сдвига по фазе  необходимо вначале комплексное сопротивление представить через его реальную и мнимую части согласно (6.54). Найти указанные части можно в результате следующих преобразований, выполняемых по правилам преобразования комплексных чисел:

. (6.60)

Очевидно, что тогда

. (6.61)

Откуда в силу (6.56) следует искомое соотношение для сдвига по фазе

. (6.62)

Из соотношений (6.59) и (6.62) видно, что полное сопротивление параллельного соединения резистора и катушки индуктивности зависит от частоты ω подводимого к этому соединению напряжения. То же справедливо и для сдвига по фазе между напряжением и результирующим током рассматриваемого соединения.

Завершая рассмотрение данного примера, обратим внимание на одну особенность рассматриваемой электрической цепи. Ее активное r и реактивное х сопротивления зависят от частоты подводимого напряжения. Можно показать, что такой особенностью обладают и другие электрической цепи, содержащие в своем составе реактивные элементы.