Введение

Учебное пособие предназначено для студентов дневной и заочной форм обучения специальности “Управление и информатика в технических системах” (220200) при изучении дисциплины “Электромашинные средства автоматизации и управления”. Пособие может быть использовано также при изучении тех дисциплин, в которых рассматриваются принципы построения электромашинных устройств и их математических моделей как элементов автоматики.

Электромашинными называются такие устройства автоматики, в которых осуществляется преобразование электрической энергии в механическую энергию (или наоборот), основанное на явлении электромагнетизма.

При изучении принципа действия и конструкции электромашинных устройств автоматики требуется, таким образом, достаточно глубокое знание теории электромагнетизма.

При изучении электромашинных устройств автоматики весьма важными являются также вопросы построения математических моделей этих устройств как элементов систем автоматики. Такие модели позволяют, в частности, на этапе разработки системы автоматики синтезировать структуру и параметры регулирующих устройств, определить правильность функционирования системы автоматики в целом и оценить ее основные технические характеристики, например, время регулирования, перерегулирование, запасы устойчивости. Таким образом, уже на этапе проектирования оказывается возможным при наличии указанных моделей оценить эффективность принятых технических решений, что позволяет снизить последующие материальные и трудовые затраты на воплощение разрабатываемой системы автоматики в ‘‘металле’’, а также на ее испытания.

При построении моделей электромашинных устройств, как и при изучении их принципа действия, используются, прежде всего, законы электромагнетизма, а также вытекающие из этих законов инженерные методы электромагнитного расчета электромашинных устройств. Поэтому усвоение основных понятий теории электромагнетизма и электромагнитного расчета электромашинных устройств является основным условием успешного изучения теории указанных устройств.

1. Понятие магнитного поля. Магнитные величины и их единицы

Магнитное поле – одна из двух сторон электромагнитного поля, характеризующаяся силовым воздействием на движущуюся электрически заряженную частицу с силой, прямо пропорциональной заряду частицы и её скорости [1, с. 2].

Указанную в определении силу будем называть, следуя [2, с. 105], электромагнитной силой.

Из приведенного определения вытекает, что на неподвижный заряд электромагнитная сила не действует, а появляется только при движении заряда и возрастает прямо пропорционально скорости заряда. Обратим внимание на то обстоятельство, что данное определение указывает принципы выявления магнитного поля в данной точке пространства. Сформулировать эти принципы предлагается самостоятельно. При этом необходимо вспомнить, что на электрический заряд действует также сила и со стороны электрического поля. Но эта сила в отличие от электромагнитной силы не зависит от скорости движения заряда и, в частности, является ненулевой при неподвижном состоянии заряда.

Магнитная индукция. Приведенное определение магнитного поля дает качественные представления об основных свойствах и отличительных особенностях этого поля. При переходе к количественным представлениям о магнитном поле необходимо вспомнить, прежде всего, что в теории электромагнетизма установлены следующие факты.

Во-первых, установлено, что модуль электромагнитной силы, действующей в некоторой точке магнитного поля, зависит не только от модуля вектора скорости, но и от направления этого вектора в рассматриваемой точке. Причём для каждой точки магнитного поля существует своя единственная плоскость, при нахождении в которой вектора скорости заряда модуль магнитной силы достигает максимума F_m. Максимум F_m электромагнитной силы, как и её произвольное значение, что указывалось в определении магнитного поля, прямо пропорционален величине заряда q и прямо пропорционален модулю V скорости заряда, т. е. справедливо

F_m= kqV,

где k – коэффициент. В теории магнитного поля коэффициент k из приведённого равенства называется магнитной индукцией и обозначается символом В.

Таким образом, последнее равенство можно записать в виде

F_m= ВqV. (1.1)

Во-вторых, установлено, что для каждой точки магнитного поля существует своя единственная прямая, при совпадении с которой вектора скорости заряда модуль электромагнитной силы F = 0.

В-третьих, установлено, векторы и всегда взаимно перпендикулярны, т.е. магнитное поле не разгоняет заряд, а лишь изменяет направление его движения.

Перечисленные факты показывают, что в магнитном поле существуют особые силовые направления, т.е. направления, связанные с его силовым воздействием, которые следует каким-то образом описывать. В теории электромагнетизма показано, что описание этих силовых направлений может быть возложено на магнитную индукцию, если ее считать векторной величиной, модуль и направление которой определяются следующим образом. Модуль вектора определяется из соотношения (1.1), а направление этого вектора совпадает с прямой, при движении заряда вдоль которой электромагнитная сила F = 0. В теории электромагнетизма показано также, что при этих предположениях соотношение для определения вектора электромагнитной силы представляет собой следующее векторное произведение:

. (1.2)

На рис. 1.1 представлена геометрическая иллюстрация векторного произведения (1.2).

Рис. 1.1. Взаимное расположение

векторов , ,

Напомним, что по определению векторного произведения, модуль F магнитной силы задается соотношением

F = qVBsin  

где  – угол между векторами и , отсчитываемый от вектора к вектору .

Из (1.3), в частности, следует, что при  = 0 или  = 180⁰ электромагнитная сила F = 0, т.е. при движении частицы по направлению магнитной индукции, как это и отмечалось выше, электромагнитная сила отсутствует, а при  = 90⁰ или  = 270⁰ абсолютное значение модуля магнитной силы достигает максимума F_m.

Напомним, что электромагнитная сила является магнитной составляющей силы Лоренца , действующей на заряд в электромагнитном поле. Другая составляющая силы Лоренца (электрическая) обусловлена силовым воздействием электрического поля на заряд и задаётся равенством

, (1.4)

где – электрическая составляющая силы Лоренца; – напряженность электрического поля.

Сила Лоренца складывается из указанных двух составляющих и определяется равенством [2, c. 27]

. (1.5)

Векторы и определяют силовые воздействия соответственно магнитного и электрического полей на заряд. В этой связи эти векторы называют силовыми характеристиками соответственно электрического и магнитного полей. Заметим, что по аналогии с напряженностью следовало бы назвать вектор напряженностью магнитного поля. Однако по историческим причинам основную силовую характеристику магнитного поля назвали магнитной индукцией [3, c. 254].

При технических исследованиях магнитного поля для определения электромагнитной силы или магнитной индукции используется проводник с электрическим током. Это объясняется тем, что ток, как известно, представляет собой направленный поток движущихся электрических зарядов. Нетрудно показать [2, c. 26], опираясь на равенство (1.3), что электромагнитная сила dF, действующая на элемент dl (см. рис. 1.2) проводника с током, вблизи которого можно принять, что магнитная индукция неизменна, задается соотношением

 

где dF – электромагнитная сила; I – сила тока в проводнике; dl – длина проводника; – угол между положительными направлениями тока I и вектора , отсчитываемый от положительного направления тока I к положительному направлению вектора .

Действительно, пусть элемент dl содержит некоторый заряд dq, который движется со скоростью в положительном направлении тока I. Тогда согласно (1.3) получим, что

dF = dqVBsin  (1.7)

Время dt, в течение которого заряд пройдёт расстояние dl, очевидно, можно определить так: dt=dl/V. Откуда следует, что

.

Вспомнив далее, что по определению ток I = dq/dt, получим

dq = Idt .

Подставив последние два равенства в (1.7), получим соотношение (1.6), что и требовалось показать.

Соотношение (1.6) представляет собой закон Ампера в скалярной форме [4, с. 19; 5, с. 275].

Закон Ампера позволяет дать достаточно практичную формулировку физического смысла вектора магнитной индукции , учитывая, что при  = 90° сила dF достигает максимума dFmax, а при  = 0 dF = 0. Тогда магнитная индукция , действующая в некоторой точке магнитного поля – это вектор со следующими свойствами. Направление вектора совпадает с осевой линией пробного проводника с током, помещенного в данную точку таким образом, что электромагнитная сила, действующая на этот проводник, равна нулю, а модуль вектора равен отношению максимально возможной электромагнитной силы dFmax , действующей в данной точке на указанный проводник, и произведения величин I и dl.

Определение направления электромагнитной силы , действующей на проводник с током в магнитном поле, можно произвести с помощью правила левой руки, которое формулируется следующим образом. Если левую руку расположить так, чтобы нормальная к току проводника составляющая вектора магнитной индукции входила в ладонь, а ладонь была направлена по току в проводнике, то тогда отогнутый в плоскости ладони на 90⁰ большой палец укажет направление электромагнитной силы, действующей на этот проводник [4, с. 20].

Действие правила левой руки иллюстрирует рис. 1.2.

Для характеристики всего множества векторов магнитной индукции некоторого заданного магнитного поля используются линии магнитной индукции.

Линия, в каждой точке которой касательная совпадает с вектором магнитной индукции, действующей в этой же точке, называется линией магнитной индукции.

Линии магнитной индукции именуются в ряде изданий силовыми линиями магнитного поля. Линии магнитной индукции придаётся положительное направление, совпадающее с направлением какого-либо вектора магнитной индукции, касающегося этой линии.

Линия магнитной индукции позволяет определить направление вектора в любой точке этой линии (рис. 1.3, а). Можно решить и обратную задачу: построить линию магнитной индукции или её часть по нескольким векторам магнитной индукции (рис. 1.3, б).

Рис. 1.3. Схемы определения направлений векторов по направлению линии магнитной индукции (а) и направления линии

магнитной индукции по направлению векторов (б)

Линии магнитной индукции прямолинейного проводника бесконечной длины с током (в отсутствии иных магнитных полей) представляют собой совокупность концентрических окружностей (см. рис. 1.4, а), лежащих в плоскости, которая перпендикулярна проводнику, и имеющих центр, который лежит на оси проводника. Проводник на рис. 1.4, а изображен в поперечном разрезе и имеет форму круга. «Косой крест» в центре этого круга показывает направление тока в проводнике. Положительные направления тока и линий магнитной индукции связаны правилом правого винта (буравчика, штопора) [4, с. 9; 6, с. 136], которое применительно к данному случаю формулируется так. Если при завинчивании правого винта (буравчика) его острие движется в положительном направлении тока, а положительное направление линии магнитной индукции совпадает с направлением вращения головки этого винта (рукоятки буравчика), то говорят, что указанные направления связаны правилом правого винта.

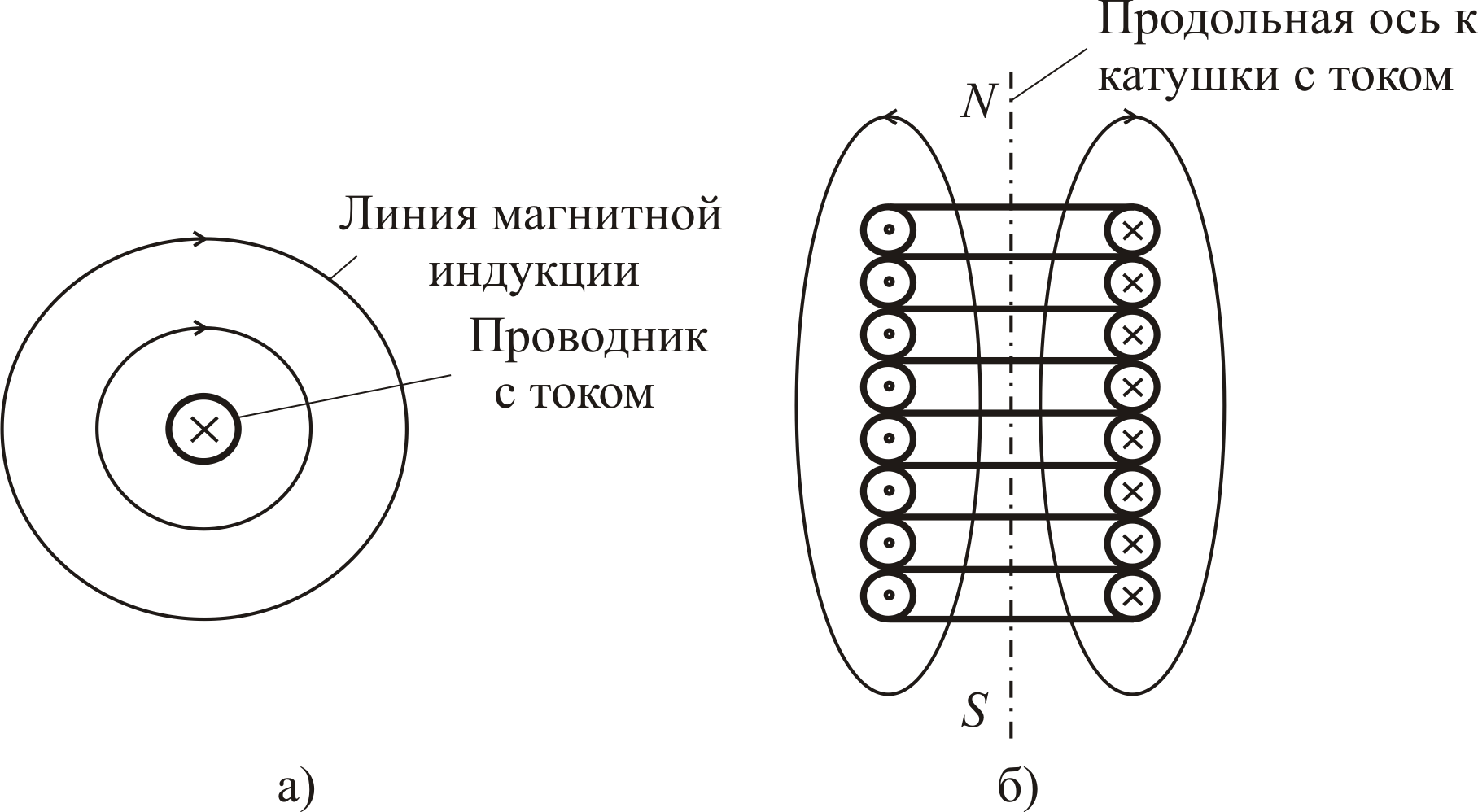
Рис. 1.4. Линии магнитной индукции прямолинейного проводника

бесконечной длины с током (а) и катушки с током (б)

Картина линий магнитной индукции катушки с током поясняется рис. 1.4, б. Здесь катушка изображена в разрезе, который сделан вдоль осевой линии катушки. Каждый виток катушки на разрезе представлен двумя окружностями, расположенными симметрично относительно осевой линии катушки. Знаки «точка» и «косой крест» указывают направления токов в витках катушки. Направления токов и линий магнитной индукции связаны правилом правого винта. Напомним, что на том конце катушки, из которого линии магнитной индукции выходят, образуется северный полюс N катушки, а в который входят – южный полюс S катушки [6, с. 137]. Напомним также, что аналогичный вид имеет магнитное поле полосового магнита.

Магнитное поле называется однородным, если в каждой точке этого поля = const (т.е. константа). Геометрически такое поле изображают прямыми параллельными линиями, расположенными на равных расстояниях друг от друга (рис. 1.5).

Такое изображение поля не противоречит свойству замкнутости линий магнитной индукции в предположении, что однородное поле есть часть некоторого общего магнитного поля, обладающего замкнутыми линиями магнитной индукции, либо при условии, что эти линии замыкаются на бесконечности.

Магнитный момент тока. Рассмотрим некоторый плоский контур C, ограничивающий собой площадь S (рис. 1.6).

Будем полагать, что по контуру протекает ток I. Введём единичный вектор , нормальный к плоскости, которой принадлежит контур C. За положительное направление вектора примем направление, связанное с положительным направлением тока I правилом правого винта (буравчика). То есть будем считать, что если при завинчивании правого винта направить движение его острия по вектору , то вращение головки винта совпадёт с направлением тока I.

Магнитный момент тока обозначается символом и задаётся равенством [2, c. 84; 3, c. 227]

. (1.8)

В силу (1.8) векторы и имеют одинаковое направление. Поэтому положительное направление магнитного момента связано, как и для вектора , с положительным направлением тока I правилом правого винта (см. рис. 1.6).

Заметим, что направление вектора совпадает с направлением (внутри контура C) линий магнитных индукций, созданных током I, а модуль m магнитного момента этого тока тем больше, чем больше ток I, и, следовательно, чем больше интенсивность магнитного поля. Таким образом, магнитный момент тока I является обобщенной характеристикой (по направлению и интенсивности) магнитного поля плоского контура, по границе которого протекает электрический ток I.

Магнитная постоянная. Магнитная постоянная обозначается символом _и имеет в СИ следующее значение:

Гн/м. (1.9)

Намагниченность и напряженность магнитного поля. Напомним, что между магнитным полем и электрическим током существует неразрывная взаимосвязь: магнитное поле при своём изменении порождает электрический ток, а электрический ток порождает магнитное поле. Для характеристики этой неразрывной взаимосвязи вводят две физические величины: намагниченность и напряженность магнитного поля. Введение этих двух величин обусловлено разделением электрического тока на две группы: макроскопические токи и молекулярные токи [2, c. 84].

Молекулярные токи – это электрические токи, обусловленные движением электрически заряженных элементарных частиц в атомах и молекулах. Молекулярные токи называют также элементарными токами [3, c. 250].

Для характеристики взаимосвязи молекулярных токов и созданного этими токами магнитного поля используется такая физическая величина как намагниченность. Намагниченность обозначается согласно ГОСТ 13494–77 символом . Во многих литературных источниках и более ранних редакциях ГОСТ, а также в данном пособии для обозначения намагниченности используется символ .

Дадим определение намагниченности . Предположим, что рассматривается некоторое вещество объёмом V (рис. 1.7), в котором движением элементарных заряженных частиц по замкнутым траекториям созданы молекулярные токи i_k, создающие магнитные моменты m_k, k = 1, ..., N , где N – количество частиц.

Намагниченностью некоторого объёма V вещества называют отношение суммы магнитных моментов молекулярных токов, занимающих этот объём вещества, к указанному объёму, что математически можно записать следующей формулой:

. (1.10)

Макроскопическими называют токи проводимости, переноса и электрического смещения.

Примером токов проводимости является направленное движение электронов в проводниках, токов переноса – движение заряженных частиц в вакуумных приборах от одного электрода к другому, а токов смещения – движение зарядов при поляризации молекул.

Для характеристики взаимосвязи макроскопических токов и созданного этими токами магнитного поля используется напряженность магнитного поля, обозначаемая символом . Понятие напряженности магнитного поля вводится следующим образом [7, с. 9; 8, с. 26; 9, с. 84].

Напряженностью магнитного поля называется векторная величина, равная разности вектора магнитной индукции , делённого на магнитную постоянную, и вектора намагниченности , что математически записывается так:

. (1.11)

Напомним, что напряженность и макроскопические токи связаны законом полного тока

, (1.12)

где = Hdlcos  – скалярное произведение векторов и , действующих в некоторой точке произвольно заданного бесконечно малого участка dl, принадлежащего контуру l; – вектор, имеющий длину dl и направленный в указанной выше точке участка dl по касательной к контуру l (см. рис. 1.8, а);  – угол между векторами и ; i_n – n-й ток, охватываемый замкнутым контуром l; n₀ – общее количество токов, охватываемых контуром l (положительные направления указанных токов связаны с направлением обхода контура l правилом правого винта). Взаимное расположение замкнутого указанного контура l и токов i_n(n = 1, ..., n₀) с указанием положительных направлений этих токов представлено на рис. 1.8, а.

Рис. 1.8. Графические пояснения к закону полного тока

Сумма токов в правой части соотношения (1.12) называется полным током, что и обусловливает название данного закона. Напомним далее [7, c.187, 506], что интеграл в (1.12) называется циркуляцией вектора вдоль замкнутого контура l.

Используя последние два понятия, закон полного тока можно сформулировать так: циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна полному току, который охватывается этим контуром [6, c. 163].

Приведем пример записи закона полного тока для контура и токов, изображенных на рис.1.8, б. Закон полного тока для данного примера запишется в следующем виде:

.

Циркуляция вектора напряженности магнитного поля вдоль замкнутого контура l может быть рассчитана, учитывая, что приближенно интеграл есть сумма, по следующей формуле (см. рис. 1.8, б):

,

где n – количество сторон произвольно вписанного в контур l многоугольника (см.рис. 1.8, б, где показаны две стороны многоугольника: (i–1)-я и i-я); H_i – длина вектора , действующего на стыке (i–1)-го и i-го участков; l_i – длина i-й стороны вписанного многоугольника; _i – угол между положительным направлением i-й стороны и вектором .

Относительная и абсолютная магнитные проницаемости. Из соотношения (1.11) следует, что для любой точки магнитного поля

. (1.13)

Зададим для произвольной точки магнитного поля некоторое направление, на которое спроектируем векторы , и . Пусть величины B, H и J есть проекции соответственно векторов , и на указанное направление. Тогда, как это известно, из аналитической геометрии, если векторы , и связаны равенством (1.13), то их проекции на некоторое направление связаны равенством

B = _ (H + J). (1.14)

Вынесем в (1.14) напряженность H за скобки, в результате чего получим

B = _H(1 + J/H).

Введя обозначение

 = J/H, (1.15)

где  – магнитная восприимчивость (символ  читается “хи”), получим из последних двух равенств соотношение

B = _.

Откуда с учетом обозначения

_r = 1 +  (1.15а)

следует, что

B = __r H. (1.16)

Величина _r называется относительной магнитной проницаемостью вещества.

Введем обозначение

_a = __r. (1.17)

Величина _a называется абсолютной магнитной проницаемостью вещества.

Соотношение (1.16) с учетом (1.17) можно преобразовать к виду

B = _aH. (1.18)

Заметим, что согласно (1.16) и (1.18) относительная _r и абсолютная _a магнитные проницаемости могут быть определены из следующих соотношений:

_r = B /(_H), (1.19)

_a = B / H. (1.20)

Эти соотношения используются, например, для расчетного определения относительной и абсолютной магнитных проницаемостей в некоторой точке исследуемого вещества в том случае, если имеются экспериментальные данные о магнитной индукции и напряженности магнитного поля в той же точке данного вещества.

Магнитный поток. Магнитным потоком называется поток вектора магнитной индукции [1]. Магнитный поток обозначается символом Ф и задается аналитически по­верхностным интегралом следующего вида:

, (1.21)

где S – поверхность интегрирования; = BdS cos – скалярное произведение векторов и ; – вектор магнитной индукции, действующей в произвольной точке бесконечно малой площадки, которая принадлежит поверхности S и имеет бесконечно малую площадь dS; – вектор, имеющий длину dS и направленный по нормали к поверхности S в той точке, где действует указанный выше вектор магнитной индукции ;  – угол между векторами и .

Напомним, что нормалью к поверхности в некоторой ее точке называется прямая, проходящая в указанной точке перпендикулярно плоскости, которая является касательной к данной поверхности в рассматриваемой точке.

Приближенно магнитный поток Ф вычисляют следующим образом (см. рис. 1.9, а).

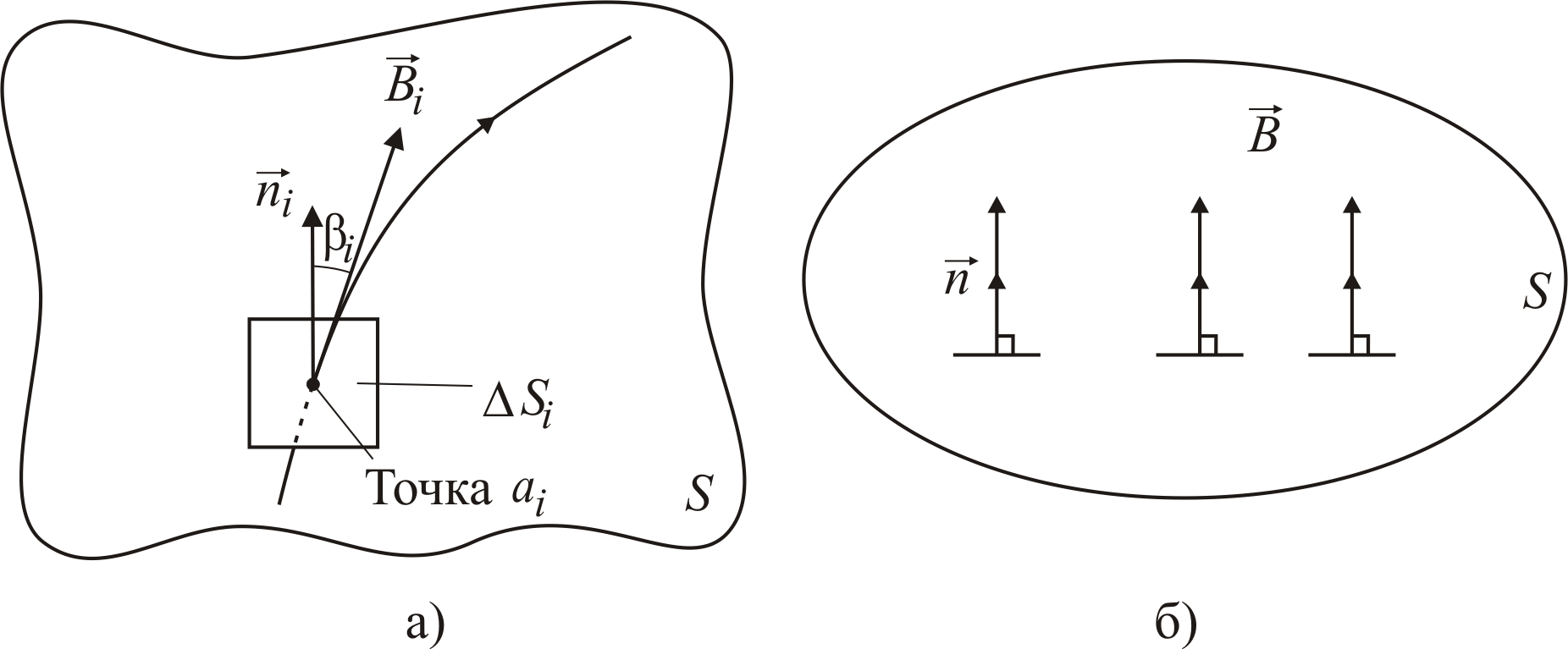
Рис. 1.9. К приближенному определению магнитного потока Ф (а) и

определению магнитного потока Ф однородного магнитного поля (б)

Вначале разбивают поверхность S на т элементарных площадок S_i, где i = 1, ... , т. Затем для каждой i-й площадки вычисляют произведение

B_i S_i cos _i,

где B_i – модуль магнитной индукции в некоторой произвольно выбранной точке a_i , принадлежащей i-й площадке; S_i – площадь i-й площадки; _i – угол между векторами B_i и n_i; n_i – единичный вектор, направленный по нормали к поверхности i-й площадки в точке a_i. Тогда получим, что

.

В случае однородного магнитного поля (см. рис. 1.9, б) магнитный поток Ф, пронизывающий плоскую поверхность площадью S при условии, что магнитная индукция перпендикулярна этой плоской поверхности, задается ра­венством

Ф = BS. (1.22)

Это равенство вытекает из соотношения (1.21). Действительно, = BdS cos. Так как по условию векторы перпендикулярны заданной плоской поверхности в каждой ее точке, то во всех этих точках углы  = 0, а cos = 1. По условию однородности магнитного поля во всех точках плоской поверхности B = const. С учетом изложенного можно записать следующую последовательность равенств:

.

Известно, что = S. Поэтому Ф = BS, что и требовалось показать.

Закон Био-Савара-Лапласа. Этот закон позволяет вычислить вектор магнитной индукции в некоторой точке магнитного поля, созданного в вакууме током I, протекающим по проводнику бесконечно малой длины dl, при условии, что проводник и точка находятся на расстоянии r. Математически закон Био-Савара-Лапласа записывается так [4, с. 15–18; 8, с. 221]:

,

где – вектор, имеющий длину dl и направленный по току I; – вектор, имеющий длину r и соединяющий точку расположения проводника dl и точку, в которой рассчитывается магнитная индукция (см. рис. 1.10).

Используя закон Био-Савара-Лапласа, можно вычислить результирующую магнитную индукцию магнитного поля, создаваемого любым количеством элементарных проводников, по которым, вообще говоря, могут протекать различные токи. Такое вычисление оказывается возможным, однако, при условии, что для исследуемого магнитного поля справедлив принцип суперпозиции (или принцип наложения).

О сущности принципа суперпозиции для магнитных полей напомним следующее. Пусть существует несколько магнитных полей, каждое из которых при отсутствии других полей характеризуется в некоторой точке пространства своим вектором магнитной индукции. Если для результирующего магнитного поля вектор магнитной индукции в указанной точке представляет собой векторную сумму магнитных индукций исходных полей, то говорят, что в указанной точке магнитного поля выполняется принцип суперпозиции для магнитной индукции.

Потокосцепление. Понятие потокосцепления вводится для электрических замкнутых цепей и обозначается символом .

Потокосцеплением замкнутой электрической цепи называют сумму магнитных потоков, пронизывающих всю поверхность, ограничиваемую внешним контуром этой цепи.

Потокосцепление используется, прежде всего, в законе электромагнитной индукции, который формулируется следующим образом. ЭДС е, индуктируемая в некотором замкнутом электрическом контуре магнитным полем, численно равна скорости изменения потокосцепления  этого контура, взятой со знаком минус.

Математически закон электромагнитной индукции записывается так:

е = – d/dt . (1.23)

Знак минус в этом законе записывается тогда, когда положительные направления ЭДС индукции е и линий магнитной индукции магнитного поля, вызвавшего эту ЭДС, связаны правилом правого винта. В противном случае перед величиной d/dt следует записывать знак плюс.

В случае одновиткового контура произвольной формы его потокосцепление  совпадает с магнитным потоком Ф, пронизывающим поверхность, которая ограничивается данным контуром, т.е.  = Ф.

В случае обмотки (см. рис. 1.11), состоящей из некоторого количества идентичных витков и имеющей форму пустотелого цилиндра, потокосцепление можно определить приближенно по формуле

, (1.24)

где W – количество витков; Ф – магнитный поток одного витка.

Приближенность соотношения (1.24) обусловлена тем, что оно не учитывает магнитный поток Ф₀, пронизывающий поверхность S₀ между двумя проводниками, соединяющими катушку с источником электроэнергии (см. рис. 1.11). Но этот поток Ф₀, создаваемый магнитной индукцией B₀, ничтожно мал. Поэтому полагают, что равенство (1.24) выполняется точно.

Закон электромагнитной индукции является основой для определения ЭДС индукции е_пр, возникающей в проводнике длиной dl, который движется поступательно со скоростью в магнитном поле с магнитной индукцией . Можно показать, опираясь на закон электромагнитной индукции, что абсолютное значение ЭДС индукции е_пр задается равенством

е_пр = BVdl sin , (1.25)

где  – наименьший угол между векторами и , а направление определяется правилом правой руки.

Правило правой руки формулируется так: если ладонь правой руки расположить так, что линии магнитной индукции будут входить в ладонь, а большой палец, отставленный в плоскости ладони на 90^o, будет показывать направление движения проводника в магнитном поле, то четыре пальца ладони покажут направление ЭДС е_пр, возникающей в этом проводнике.

Из соотношения для ЭДС индукции е_пр следует, что при   0 ЭДС , а при  = 0 ЭДС е_пр= 0, т.е. приходим к следующему выводу. Если проводник при своем движении пересекает линии магнитной индукции, то в нем наводится ненулевая ЭДС, а если проводник движется вдоль линий магнитной индукции ( = 0), то ЭДС в нем не наводится.

Продолжим рассмотрение понятия потокосцепления. Различают потокосцепление самоиндукции (или собственное потокосцепление) и потокосцепление взаимной индукции ( или взаимное потокосцепление) электрической цепи [1; 6, с. 149, 152].

Собственным потокосцеплением электрической цепи называют ее потокосцепление, обусловленное магнитным полем только того тока, который протекает по данной цепи. Собственное потокосцепление будем обозначать символом _L.

Взаимным потокосцеплением электрической цепи называют ее потокосцепление, обусловленное внешними магнитными полями. Взаимное потокосцепление будем обозначать символом _.

При рассмотрении двух электрических цепей взаимное потокосцепление обозначают символом _kj, где k – номер цепи, для которой определяется взаимное потокосцепление; j – номер цепи, ток которой обусловливает потокосцепление _kj [2].

В общем случае потокосцепление электрической цепи складывается из собственного и взаимного потокосцеплений. Символ используется в тех случаях, когда учитываются оба вида потокосцепления.

Собственная индуктивность электрической цепи. Обозначается собственная индуктивность символом L. Собственной индуктивностью или индуктивностью электрической цепи называют отношение мгновенного собственного потокосцепления _L этой цепи к протекающему по данной цепи мгновенному току i, вызвавшему указанное собственное потокосцепление, т. е.

L = _L/i. (1.26)

Правая часть равенства (1.26) записывается со знаком плюс тогда, когда положительные направления тока i и линий магнитной индукции магнитного поля, созданного этим током i, связаны правилом правого винта. В противном случае в правой части равенства (1.26) следует записывать знак минус.

Взаимная индуктивность. Это понятие вводится для двух электрических цепей, между которыми существует магнитная взаимосвязь [1]. Допустим, что в первой цепи протекает ток i₁, который обусловливает для второй цепи взаимное потокосцепление ₂₁. Тогда взаимной индуктивностью называется величина M₂₁, задаваемая следующим соотношением:

. (1.27)

Взаимодействие тех же двух цепей можно охарактеризовать и другой взаимной индуктивностью. Допустим, что во второй цепи протекает ток i₂, который обусловливает для первой цепи взаимное потокосцепление ₁₂. Тогда по аналогии можно ввести взаимную индуктивность M₁₂, задавая ее следующим равенством:

. (1.28)

В теории электромагнетизма показано, что если для магнитного поля, справедлив принцип суперпозиции в отношении результирующих векторов , , [6, с. 153], то

M₁₂ = M₂₁. (1.29)

Принцип суперпозиции был изложен выше для магнитной индукции. Аналогично принцип суперпозиции формулируется и для векторов и .

Запишем далее весьма важное для теории машин соотношение, которое позволяет определить потокосцепление некоторой k-й обмотки (катушки), находящейся в собственном поле и поле других обмоток. Это соотношение, опирающееся на понятия взаимной и собственной индуктивностей и вытекающее из закона Био-Савара-Лапласа, имеет, как это можно показать, следующий вид:

, (1.30)

где M_kj – взаимная индуктивность k-й и j-й обмоток, , j = 1, … , n; L_k – индуктивность k-й обмотки; i_j – ток j-й обмотки, j = 1, … , n.

Ценность соотношения (1.30) заключается в том, что расчет магнитных полей машин при его использовании сводится к определению взаимных индуктивностей, которые представляют собой коэффициенты, зависящие только от относительно простых геометрических и магнитных характеристик машин.

Физический смысл относительной магнитной проницаемости вещества. Пусть имеются две одинаковые катушки, конструктивные схемы которых приведены на рис. 1.12. Одна катушка не имеет сердечника и располагается в пустоте (см. рис. 1.12, а). Другая катушка намотана на замкнутый сердечник, выполненный из некоторого вещества (см. рис. 1.12, б).

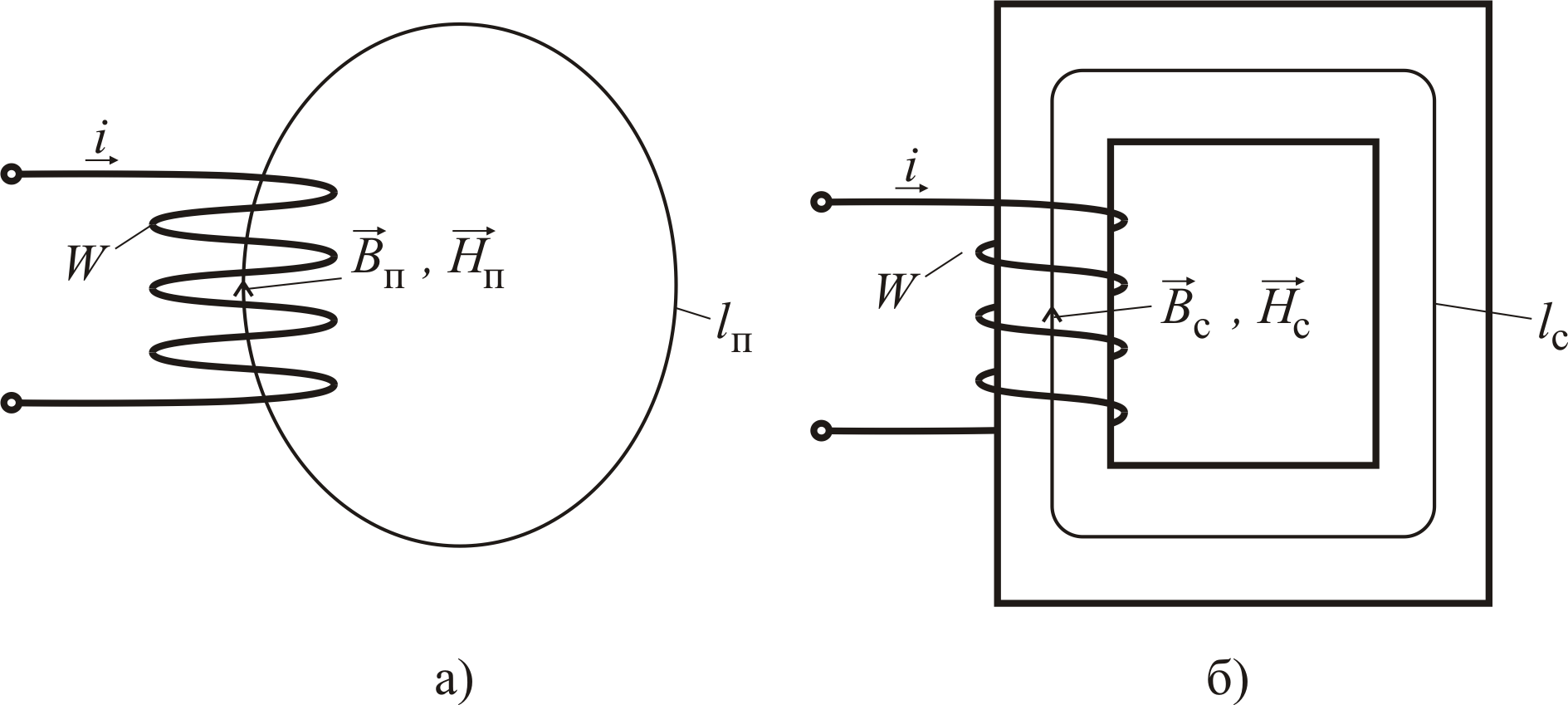
Рис. 1.12. Электромагнитные схемы двух одинаковых катушек:

без сердечника в пустоте (а) и с сердечником (б)

Пусть катушка с сердечником при протекании по ней тока i создает внутри сердечника магнитную индукцию В_с . Пусть катушка без сердечника при протекании по ней того же тока i создает внутри катушки магнитную индукцию В_п .

Покажем, что отношение магнитной индукции В_с к магнитной индукции В_п равно относительной магнитной проницаемости _rc сердечника. Иначе говоря, покажем, что относительная магнитная проницаемость _rc замкнутого сердечника катушки есть коэффициент усиления этим сердечником магнитной индукции, создаваемой данной катушкой без сердечника.

Для определения магнитных индукций В_п и В_с катушек определим вначале соответственно напряженности H_п и H_c магнитных полей, действующих внутри катушек.

При этом воспользуемся законом полного тока, принимая следующие допущения. Во-первых, в качестве замкнутых контуров выберем линии магнитной индукции l_п и l_с (см. рис. 1.12) так, чтобы l_{п } l_с. Во-вторых, будем полагать, что напряженности всех точек линии l_п одинаковы и равны H_п. В-третьих, допустим, что напряженности всех точек линии l_с одинаковы и равны H_с. Тогда на основании закона полного тока можно записать, что

H_п= iW / l_п, (1.31)

H_c = iW / l_c. (1.32)

Откуда с учетом принятого допущения, что l_{п } l_с, следует

H_{п } H_c. (1.33)

В силу (1.16) получим, что

В_п = __rп H_п, (1.34)

В_с = __rс H_с. (1.35)

Из формул (1.34) и (1.35) с учетом (1.33) после преобразований следует

. (1.36)

Вспоминая, что

, (1.37)

где J_п – намагниченность пустоты, и учитывая, что в пустоте отсутствуют атомы вещества, а значит и их магнитные поля, т.е J_п = 0, получаем согласно (1.37), что

_rп = 1. (1.38)

Тогда из (1.36) с учетом (1.38) после преобразований следует, что

. (1.39)

Это и означает, что сердечник усиливает в _rc раз магнитную индукцию В_п, создаваемую в пустоте катушкой с током.

Существуют вещества, которые могут в 10...1,5·10⁶ раз увеличивать магнитную индукцию, создаваемую реальными токами, протекающими по реальным катушкам без сердечников. Это означает, что существуют вещества, у которых _rc = 10...1,5·10⁶.

Магнитная индукция связана с целым рядом величин монотонно возрастающими зависимостями. Поэтому существенное увеличение магнитной индукции приводит и к существенному увеличению указанных величин. Так, например, магнитная индукция прямо пропорционально связана с электромагнитной силой, что приводит к существенному увеличению электромагнитных усилий катушки с током при помещении в нее сердечника. Заметим, что только при таком усилении (в 10...1,5·10⁶ раз) магнитных индукций и электромагнитных сил электромашинные устройства могут быть использованы в производственных механизмах.

Магнитная индукция определяет также магнитный поток. При этом нетрудно показать, что относительная магнитная проницаемость _rc является также коэффициентом усиления магнитного потока, создаваемого внутри катушки.

Действительно, допустив, что поля во внутренних объемах катушек однородны, получим согласно (1.22) следующие соотношения для магнитных потоков Ф_с и Ф_п катушек в их поперечных сечениях:

Ф_с=В_сS_с, (1.40)

Ф_п=В_пS_п, (1.41)

где S_п, S_с – площади поперечных сечений катушек. Так как рассматриваемые катушки принимаются идентичными, т.е. S_п= S_с, то из (1.40) и (1.41) следует, что

В_с/В_п=Ф_с/Ф_п. (1.42)

Из (1.39) и (1.42) далее нетрудно получить

, (1.43)

что и доказывает приведенное выше утверждение об усилении сердечником магнитного потока катушки с током.

Таким образом, приходим к следующим выводам.

1. Основное назначение сердечника катушки с током состоит в усилении магнитной индукции и магнитного потока, создаваемых указанным током.

2. Коэффициент усиления магнитной индукции и магнитного потока равен (в случае замкнутого сердечника) относительной магнитной проницаемости сердечника _rc.

Степень усиления веществом магнитной индукции определяется тем видом магнетизма, который реализуется в данном веществе. Изложение известных разновидностей магнетизма вещества приводится в следующем разделе.

Единицы магнитных величин. Единицы магнитных величин в системе СИ приведены в таблице «Наименования, обозначения и единицы магнитных величин» [9].

Таблица

Наименования, обозначения и единицы магнитных величин

Магнитная величина			Единица магнитной величины
Наименование	Обозначение		Наименование	Обозначение
	По ГОСТ 13494–77	В пособии		Рус­ское	Между-народное
Магнитная индукция	B	B	Тесла	Тл	Т
Магнитный момент	m	m	Ампер - квадратный метр	А·м2	Н/m
Магнитная постоянная	μ0	μ0	Генри на метр	Гн/м	H/m
Намагниченность	M	J	Ампер на метр	А/м	A/m
Напряженность магнитного поля	H	H	Ампер на метр	А/м	A/m
Магнитная восприимчивость			Безразмерная	–	–
Относительная магнитная проницаемость	μ r	μ r	Безразмерная	–	–
Абсолютная магнитная проницаемость	a, 	a	Генри на метр	Гн/м	H/m
Магнитный поток	Ф	Ф	Вебер	Вб	Wb
Потокосцепление	Ψ	Ψ	Вебер	Вб	Wb
Собственная индуктивность	L	L	Генри	Гн	H
Взаимная индуктивность	M	M	Генри	Гн	H