1. Особенности применения и задачи кластерного анализа. Виды расстояний между объектами и их особенности.

Исследователь располагает информацией:

• n - подлежащих классификации наблюдений, заданных матрицей X, размерности nxp.

• Отсутствует априорная информация о характере распределения наблюдений X_i (i=1,2,…,n)

• Отсутствуют обучающие выборки

Общая постановка задачи автоматической классификации

Всю анализируемую совокупность объектов , представленную в виде

• матрицы наблюдений X «объект-свойство»,

• либо матрицы парных расстояний R

разбить на сравнительно небольшое число однородных, в определенном смысле, групп или классов.

При этом априорная информация о количестве кластеров и их характеристиках отсутствует

Решение задачи заключается в определении естественного расслоения исходных наблюдений на четко выраженные кластеры, лежащие друг от друга на некотором расстоянии.

Наиболее трудным и менее формализованным является определение понятие однородности объектов.

Для этого вводят понятие

• расстояния между объектами d_ij = d (О_i,О_j) – расстояние между О_i и О_j объектами

• степень близости (сходства) d_ij i-го объекта к j-му

Выбор метрики или меры близости является узловым моментом исследования, от которого зависит окончательный вариант разбиения объектов на классы.

Выбор метрики или меры близости в каждом конкретном случае должен производиться в зависимости от:

• целей исследования,

• физической и статистической природы вектора наблюдений Х,

• априорных сведений о характере вероятностного распределения Х.

Однородность группы => генеральная совокупность с одновершинной плотностью распределения (полигоном частот). Если при этом известно, что наблюдения X_i извлекаются из нормальных генеральных совокупностей с одной и той же матрицей ковариаций ∑, то естественным является расстояние махаланобисного типа.

1.Обобщенное (взвешенное) расстояние Махаланобиса

- вектор-столбец, соответствующий i – му наблюдению

X_ij - значение j-го показателя для i-го объекта;

- симметричная неотрицательно-определенная матрица «весовых коэффициентов», которая обычно выбирается диагональной

- ковариационная матрица, соответствующая р -мерному вектору наблюдений X_i

2. Обычное Евклидово расстояние

Получается из метрики Махаланобиса в предположении, что

• элементы вектора X_i взаимно независимы и имеют одну и туже дисперсию 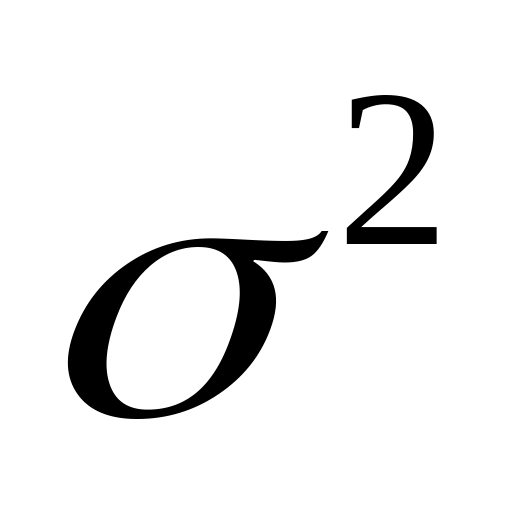, то есть

• Все показатели одинаково важны для классификации, то есть

Использование этого расстояния оправдано в следующих случаях:

а) наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение (т.е. компоненты Х взаимно независимы и имеют одну и ту же дисперсию)

б) компоненты вектора наблюдений Х однородны по физическому смыслу и одинаково важны для классификации;

в) признаковое пространство совпадает с геометрическим пространством.

3.Взвешенное Евклидово расстояние

• где w_l, “вес” пропорционально степени важности признака. Обычно принимают 0£w£1, где l=1,2,...р.

• Определение “весов”, как правило, связано с дополнительными исследованиями, например, организацией опроса экспертов и обработкой их мнений.

• Попытки определения весов только по информации, содержащейся в выборке, как правило, не дают желаемого успеха

4. Хеммингово расстояние

Используется как мера различия объектов, задаваемых дихотомическими (атрибутивными) признаками и равно числу несовпадений значений соответствующих признаков в рассматриваемых i-м и j-м объектах.