
- •Свойства транспонированных матриц
- •Умножение матриц
- •Условие существования обратной матрицы. Для того, чтобы квадратная матрица a имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.Е. DetA ≠ 0 . Метод Гаусса—Жордана
- •С помощью матрицы алгебраических дополнений
- •Метод Гаусса приведения матрицы к ступенчатому виду
- •Доказательство (условия совместности системы) Необходимость
- •]Достаточность
- •Векторная форма записи
- •Матричная форма записи
Векторная форма записи
Система уравнений может быть записана в векторном виде:
A1x1 + A2x2 + ... + Anxn =B
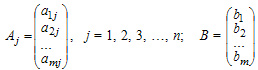
Матричная форма записи
В матричной записи система линейных уравнений может быть записана следующим образом:
AX=B
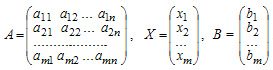
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместность см выше
15-ый вопрос
Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.
Далее не знаю----------------------------------------------------------------------------------------------------------------------------------------------------
16-ый вопрос
17-ый вопрос
18-ый вопрос
Теорема (о базисном миноре): Пусть — базисный минор матрицы , тогда:
базисные строки и базисные столбцы линейно независимы;
любая строка (столбец) матрицы есть линейная комбинация базисных строк (столбцов).Если — квадратная матрица, и , то строки и столбцы этой матрицы линейно зависимы.
Теорема 3.1 о базисном миноре. В произвольной матрице каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Действительно,
без ограничения общности предполагаем,
что в матрице
размеров
базисный
минор расположен в первых ![]() строках
и первых
столбцах.
Рассмотрим определитель
строках
и первых
столбцах.
Рассмотрим определитель
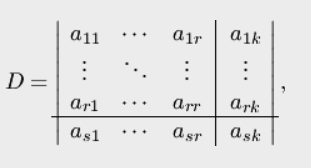
который
получен приписыванием к базисному
минору матрицы
соответствующих
элементов s-й строки и k-го столбца.
Отметим, что при любых ![]() и
и ![]() этот
определитель равен нулю. Если
этот
определитель равен нулю. Если ![]() или
или ![]() ,
то определитель
,
то определитель ![]() содержит
две одинаковых строки или два одинаковых
столбца. Если же
содержит
две одинаковых строки или два одинаковых
столбца. Если же ![]() и
и ![]() ,
то определитель
равен
нулю, так как является минором (r+l)-ro
порядка. Раскладывая определитель по
последней строке, получаем
,
то определитель
равен
нулю, так как является минором (r+l)-ro
порядка. Раскладывая определитель по
последней строке, получаем
![]()
где ![]() —
алгебраические дополнения элементов
последней строки. Заметим, что
—
алгебраические дополнения элементов
последней строки. Заметим, что ![]() ,
так как это базисный минор. Поэтому
,
так как это базисный минор. Поэтому
![]() ,
где
,
где ![]()
Записывая
последнее равенство для ![]() ,
получаем
,
получаем
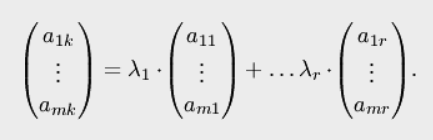
т.е. ![]() -й
столбец (при любом
)
есть линейная комбинация столбцов
базисного минора, что и требовалось
доказать.
-й
столбец (при любом
)
есть линейная комбинация столбцов
базисного минора, что и требовалось
доказать.
