§ 6. Метод вариации произвольных постоянных.
Применим
этот метод для решения ЛНС ДУ (5.1). Общее
решение ЛОС ДУ (3.1) дается формулой
где
и
- произвольные постоянные. Будем искать
решение системы (5.1) в виде
(6.1)
где
и
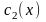- функции, подлежащие определению.
Подставим
(6.1) в (5.1):
Откуда
получаем
Аналогично
получаем второе уравнение для функций
:
.
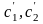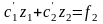Итак,
для производных
имеем систему уравнений
(6.2)
определитель
которой есть определитель Вронского
для фундаментальной системы решений
системы (3.1), который не обращается в
нуль ни в одной точке (a,b).
Поэтому решая систему (6.2), однозначно
определяются
и
:
и
.
Интегрируем эти выражения и подставляем
результат в формулу (6.1).
43) Интегрирование линейного однородного уравнения в частных производных первого порядка.
44) Решение задачи Коши для линейного однородного уравнения в частных производных.
Если
суть первые интегралы системы
то
общее решение однородного линейного
уравнения с частными производными имеет
вид
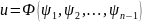где Ф-любая
функция, имеющая непрерывные частные
производные по 
Задача
Коши:
найти решение u,
удовлетворяющее условию
Составляем систему функциональных уравнений:
………..
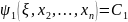
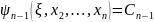
из
которой выражаем 
через
:
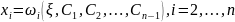Функция
и есть решение задачи Коши.