21)Линейная краевая задача. Функция Грина.

22)Приведение линейных дифференциальных уравнений к простейшему виду.

Нету((

24.Понятие нормальной системы. Теорема существования и единственности решения задачи Коши для нормальной системы. Схема доказательства.

Нормальные системы обыкновенных дифференциальных уравнений.

Определение. Совокупность соотношений вида:

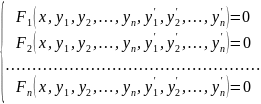
где х- независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.

Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.

Такая система имеет вид: (1)

Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.

Нормальная система в векторных обозначениях примет вид

где  .

Определение. Вектор-функция   называется решением нормальной системы (1) на промежутке  , если:

1.

2.

3.

Рассмотрим начальное условие

Точка (x0,y0) называется начальной точкой, а ее координаты x0,y0 называются начальными данными.

Определение. Задача нахождения решения нормальной системы (1), удовлетворяющего начальному условию (2), называется задачей Коши.

Система уравнений вида

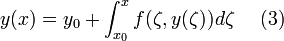
где  , называется системой интегральных уравнений.

Вектор-функция   называется решением на промежутке   системы (3), если:

1.

2.

3.

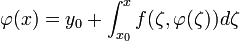
Лемма об эквивалентности. Вектор-функция   - решение задачи Коши (1) при условии (2) тогда и только тогда, когда   решение системы интегральных уравнений (3).

Теорема существования и единственности решения задачи Коши.

Пусть вектор-функция   удовлетворяет на каждом компакте области G условию Липшица

Тогда:

1) найдется такое δ > 0, что при | x − x0 | решение задачи Коши (1) при условии (2) существует,

2)решение задачи Коши единственно

В силу леммы об эквивалентности доказательство теоремы сводится к доказательству существования и единственности решения системы интегральных уравнений (3).

A)Существование

Поскольку   и G - открытое множество, то   что замкнутый цилиндр   принадлежит G. В силу того, что цилиндр Gpq компакт то

Будем строить решение системы интегральных уравнений (3) методом приближений Пикара при | x0 − x | < δ, где  . Определим последовательные приближения следующим рекурентным образом при  :

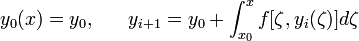
ясно, что каждая yi(x) непрерывна при (x,y), и что 

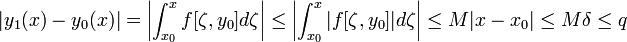
Как известно из курса анализа, равномерная сходимость функционального ряда   эквивалентна равномерной сходимости ряда вида

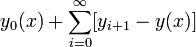
докажем оценку

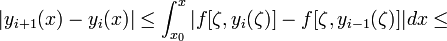
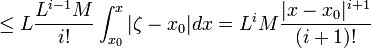
По теореме Вейршрасса получем, что

И

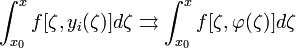
Единственность следует из леммы Гронуолла.

33.Структура общего решения линейной неоднородной системы. Метод вариации постоянных.

Определение 1. ЛНС ДУ называется система уравнений следующего вида (5.1) где - заданные непрерывные на интервале (a,b) функции.

Т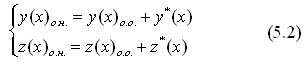 еорема 1. Общее решение ЛНС ДУ (5.1) представляет собой сумму общего решения соответствующей ЛОС ДУ (3.1) и какого-либо частного решения системы (5.1):

Доказательство.

1. Прежде всего докажем, что (5.2) является решением ЛНС ДУ (5.1). Для этого, подставим выражение (5.2) в (5.1) и покажем, что в результате получим тождество.

т.е. имеем ₀₌₀. Аналогичный вывод имеет место и для второго уравнения системы (5.1).

2. Во втором разделе доказательства докажем, что выражение (5.2) дает общее решение ЛНС. Для этого надо показать, что всегда найдутся числа такие, что выделенное из семейства (5.2) частное решение будет удовлетворять начальным условиям (5.3). Согласно теореме 2 § 3 выражение (5.2) можно переписать в виде: (5.4) где и образуют фундаментальную систему решений ЛОС ДУ. Подставим в (5.4) начальные условия: Или (5.5) Определитель этой системы уравнений есть определитель Вронского

Но согласно теореме 1 § 3 он не равен нулю , следовательно, система уравнений (5.5) имеет решение и притом единственное: . Теорема доказана.