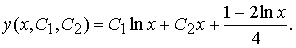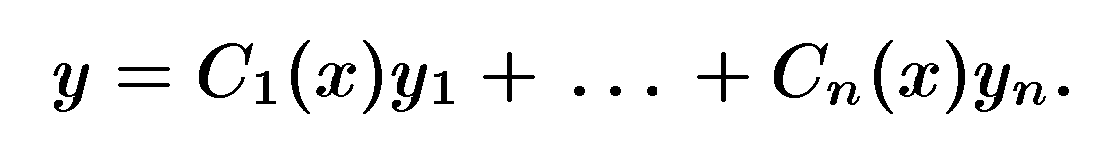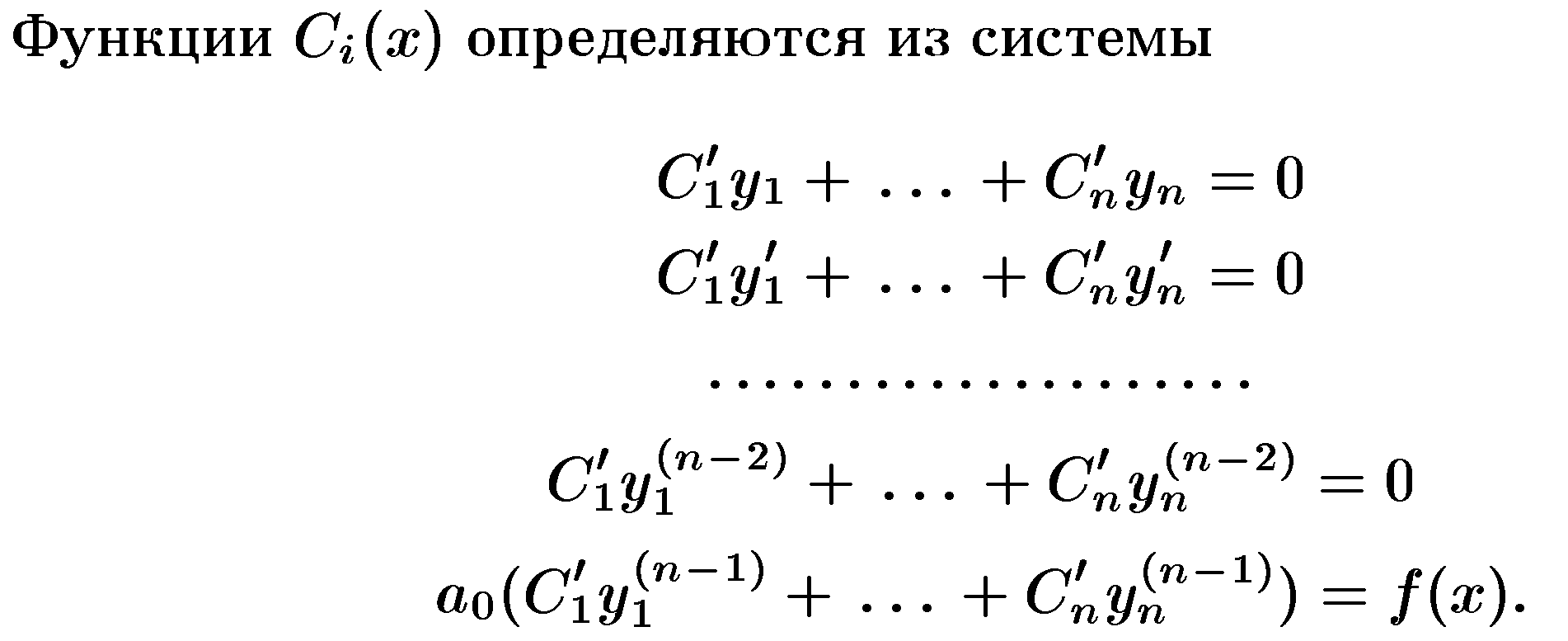16)Фундаментальная система решений. Структура общего решения линейного однородного уравнения.

Рассмотрим линейное однородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.

Иными словами любые n линейно независимых решений   y₁(x), y₂(x),..., y_n(x) уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0 образуют фундаментальную систему решений.

 

Доказано, что у однородного линейного дифференциального уравнения с непрерывными коэффициентами существует фундаментальная система решений.

Пусть задана некоторая линейно независимая система n векторов из R_n:

И пусть функции   y₁(x), y₂(x),..., y_n(x) — решения линейного однородного уравнения с начальными условиями:

Функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений линейного однородного уравнения.

Структура общего решения линейного однородного уравнения.

Рассмотрим на [a; b] линейное однородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянных C₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x,C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x),y₂(x),..., y_n(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x),

где C₁,...,C_n — произвольные постоянные.

17)Формула Остроградского – Лиувилля.

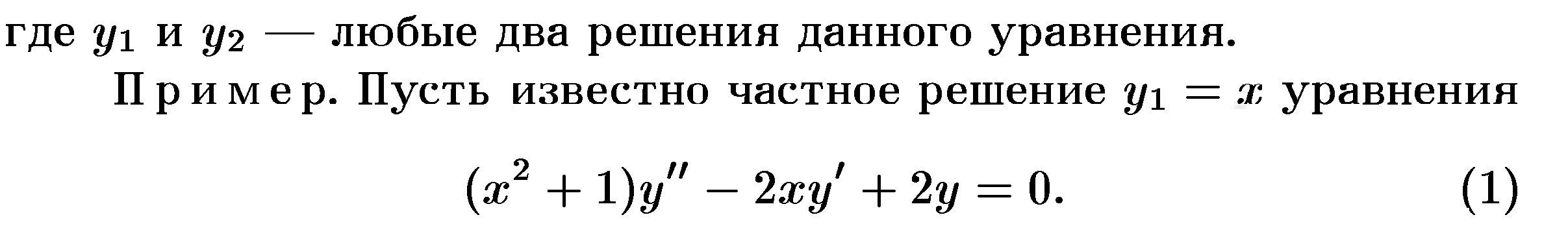
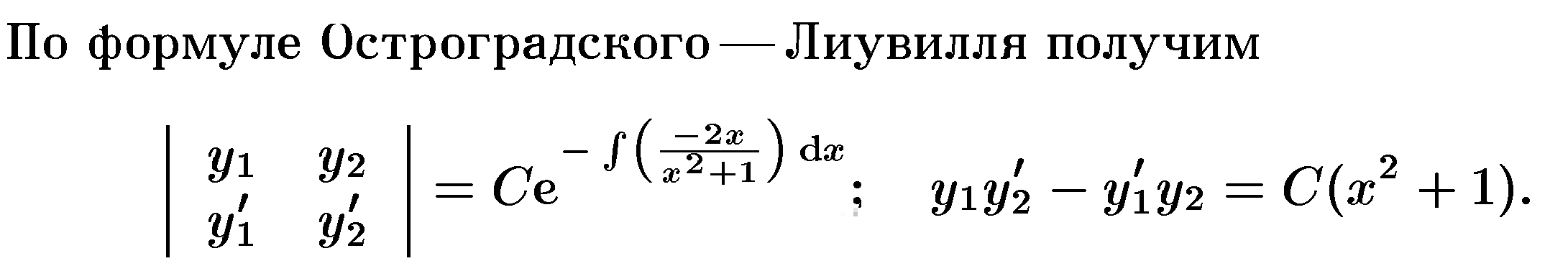
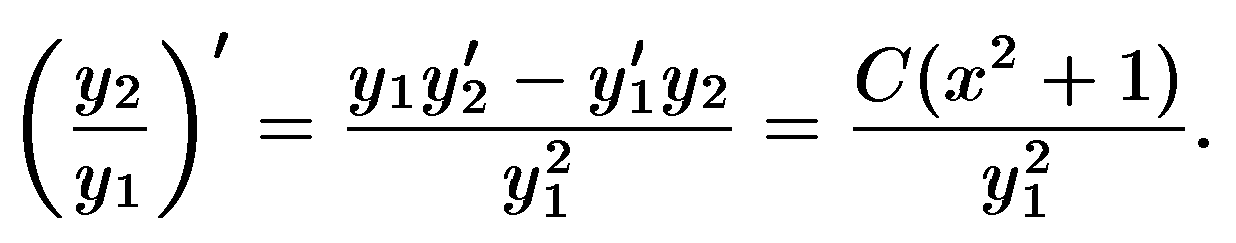
18)Линейное неоднородное уравнение. Структура общего решения. Метод вариации постоянных.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянных C₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x,C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

Справедливо следующее утверждение ( теорема о структуре общего решения линейного неоднородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x),y₂(x),..., y_n(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x) + y*(x),

где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.