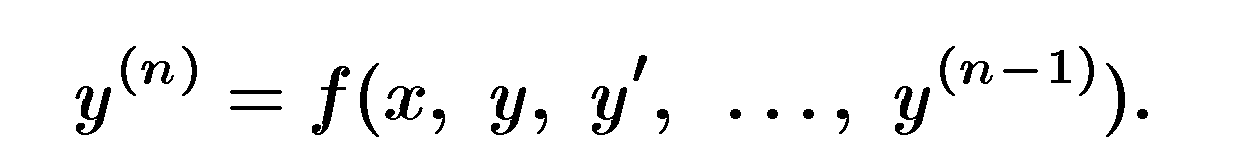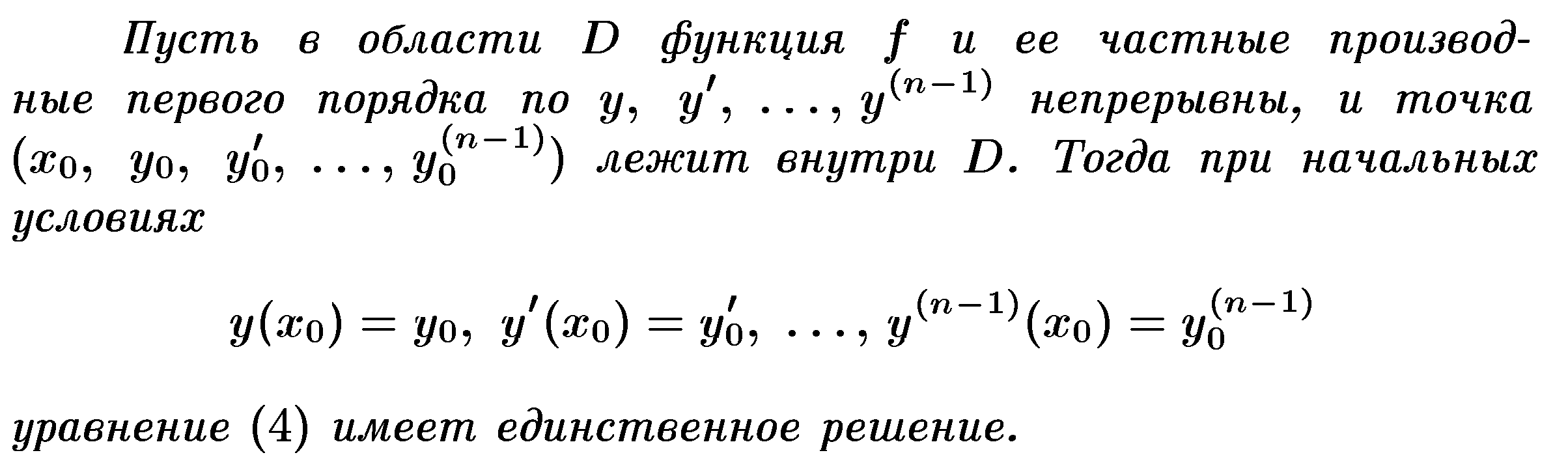7)Теорема существования и единственности решения для уравнения .

9.Уравнения Лагранжа и Клеро.

Уравнением Лагранжа называется дифференциальное уравнение, линейное относительно x и y, т.е.

уравнение вида 

A(p)y+B(p)x=C(p),p=y′,

где коэффициенты A, B, C - данные дифференцируемые функции от производной p=y′. Разрешая это уравнение относительно y (считая A(p)/=0) , приводим его к виду

y=ϕ(p)x+ψ(p).  (1)

Дифференцируя дифференциальное уравнение (1) по x, получим

dydx=p=ϕ′(p)dxdpx+ϕ(p)+ψ′(p)dxdp.   (2)

Если в (2) рассматривать x=x(p), получим линейное уравнение (при  ϕ(p)/=p) 

dydx+ϕ′(p)ϕ(p)−px=ψ′(p)p−ϕ(p).  (3)

дифференциальное уравнение (3), как известно, интегрируется в квадратурах. Пусть x=λ(p,c) его

общее решение. Тогда подставляя x=λ(p,c) в (1), находим решение уравнения Лагранжа в

параметрической форме (4):

x=λ(p,c)

y=ϕ(p)λ(p,c)+ϕ(p) 

Если из системы (4) удается исключить параметр p, то получим общий интеграл уравнения

Лагранжа в форме 

Φ(x,y,c)=0.

Случай ϕ(p)=p  надо рассмотреть отдельно. В этом случае из (1) уже нельзя получить уравнение (3).

Уравнение Клеро является частным случаем уравнения Лагранжа.Оно получается из него при ϕ(p)=p  и имеет вид 

y=px+ψ(p),  (1)

где ψ(p) - данная дифференцируемая функция. Дифференцируя обе части (1) по x, получаем

dydx=p=p+xdxdp+ψ′(p)dxdp

или [x+ψ′(p)]dxdp=0.

При dp/dx=0  получаем p=c=const и, подставляя это в (1), находим общее решение

y=cx+ψ(c).  (2)

Итак, общее решение уравнения Клеро получается из самого уравнения Клеро заменой p=y′

 на произвольную постоянную c. Решение (2) геометрически представляется семейством прямых от

одного параметра c. Пусть теперь x+ψ′(p)=0. Отсюда x=−ψ′(p)  и это подставляя в (1), находим решение уравнения Клеро в параметрической форме (3):

x=−ψ′(p) 

y=−pψ′(p)+ψ(p) 

Решение (3) не содержит произвольной постоянной и оно не получается из общего решения (2).

11.Дифференциальные уравнения го порядка. Понятие решения. Понятие общего решения и общего интеграла.

Линейные дифференциальные уравнения n-го порядка. Общая теория.

   Однородные и неоднородные линейные уравнения n-го порядка

   Линейное уравнение n-го порядка имеет следующий общий вид:

            y ⁽ⁿ⁾ + p₁ (x) y ^{(n – 1)} + … + p_{n – 1} (x) y ' + p_n (x) y = f (x).       (10.1)

   Если в рассматриваемом интервале изменения x функция f (x) тождественно равна нулю, то уравнение (10.1) принимает вид

            y ⁽ⁿ⁾ + p₁ (x) y ^{(n – 1)} + … + p_{n – 1} (x) y ' + p_n (x) y = 0.       (10.2)

и называется однородным. Если f (x) ≠ 0, то уравнение (10.1) называется неоднородным.

 Понятие о комплексном решении однородного линейного уравнения

   Для однородного линейного уравнения наряду с действительными решениями следует ввести понятие комплексного решения. Дадим сначала понятие о комплексной функции от действительной переменной. Пусть даны две действительные функции u(x) и v(x), определенные в интервале (a, b).

   Функцию

            y(x) = u(x) + iv(x ( ) i =  )      (10.6)

будем называть комплексной функцией от действительной переменной x, определенной в интервале (a, b). При этом функции u(x) и v(x) называются действительной и мнимой частями комплексной функции y(x).

   Действительная и мнимая части комплексного решения однородного линейного уравнения являются действительными решениями этого уравнения, так что знание одного комплексного решения дает возможность найти два действительных решения.

   Свойства решений однородного линейного уравнения

   Ниже увидим, что знание частных решений однородного линейного уравнения значительно облегчает (а иногда позволяет до конца решить задачу полного интегрирования этого уравнения) построение общего решения. Это оказывается возможным благодаря тому, что частные решения однородного уравнения обладают следующими замечательными свойствами:

1. Если y₁ = y₁ (x) — частное решение однородного линейного уравнения L(y) = 0, то

            y = Cy₁,

где C — произвольная постоянная, тоже является решением этого уравнения.

Таким образом, зная одно частное решение, можем (без квадратур!) получить целое (однопараметрическое) семейство решений.

Это свойство иногда выражают так: решение однородного линейного уравнения определяется с точностью до постоянного множителя.

2. Если y₁ = y₁ (x) и y₂ = y₂ (x) — частные решения однородного уравнения L(y) = 0, то их сумма

            y = y₁ + y₂

тоже является решением этого уравнения.

Наличие свойств 1 и 2 говорит о том, что множество решений однородного линейного уравнения является линейным пространством.

3. Если y₁, y₂, …, y_m — частные решения уравнения L(y) = 0, то

            y =  C_ky_k,

где C₁, C₂, …, C_m — произвольные постоянные, тоже является решением этого уравнения

12)Задача Коши для уравнения го порядка. Теорема существования и единственности решения. Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x),  …  , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число nназывается порядком уравнения. 

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

y⁽ⁿ⁾ = f(x, y, y ',  y '',  …  , y^{(n − 1)}).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. 

Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0,    x>x₀,

удовлетворяющего условиям

y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 Условия   y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1} называются начальными данными, начальными условиями или данными Коши.

 Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0, называется частным решением.

 Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1.Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Теорема существования и единственности решения для уравнения n-ого порядка.