6.Теорема существования и единственности решения задачи Коши: .

a) Сведение к эквивалентному интегральному уравнению.

б) Построение последовательных приближений.

в) Сходимость последовательных приближений.

Теорема о существовании и единственности.

Так как дифференциальное уравнения имеет бесконечное множество решений, то речь идет не о числе решений, а о том, как можно описать совокупность всех решений данного дифференциального уравнения.

Теорема. Пусть (1)

дифференциальное уравнение. Будем предполагать, что задана на некотором открытом множестве , которое принадлежит плоскости (декартовых координат). Предположим, что и непрерывны на . Тогда:

1. Для любой точки найдется решение уравнения (1), которое удовлетворяет условию (2)

2. Если два решения уравнения (1) совпадают хотя бы в одной точке , то решение и будут тождественно равны для всех значений переменной , для которых они определены.

Определение. Числа 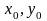называется начальными значениями для решения , а условие (2) называется начальными условиями. Теорема утверждает, что координаты могут быть начальными значениями для некоторого решения уравнения (1). Два решения с общими начальными условиями совпадают.

Геометрическая интерпретация.

Через некоторую точку Г проходит только одна интегральная кривая. Решением (1) обычно называется некоторая функция , заданная на некотором определенном интервале 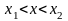. Наряду с этой функцией может быть определена функция 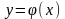, которая также является решением, но она задана на другом интервале 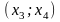. Второй пункт утверждает, что 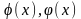совпадают на интервале, на котором они обе определены. Если полностью содержит , то решение , заданное на это есть продолжение решения . Поэтому если подразумевать под интегральной кривой график не продолжаемого решения, то утверждение о том, что через каждую точку проходит единственная кривая становится точным.

Доказательство:

1. Переход от дифференциального уравнения к интегральному.

а) Пусть некоторое решение (1) определенное на 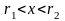,тогда выполняется тождество: (*)

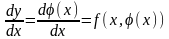при этом пусть: . Проинтегрировав (*), получим: 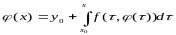. (3) Продифференцировав соотношение (3) по x, получаем (*) , то есть интегральное уравнение (3) эквивалентно дифференциальному уравнению (*) с соответствующими начальными условиями.

б) Пусть непрерывная функция, определенная на . Причем график этой функции целиком расположен в открытом множестве Г. Точка ,тогда воспользуемся правой частью тождества (3) и поставим в соответствие 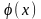некоторую функцию 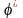, которая также определена на и 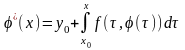(4) График в общем случае может и не принадлежать открытому множеству Г. Такая запись позволяет рассматривать правую часть (4) как оператор, который ставит в соответствие 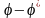, то есть . 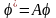(5)

Рассмотрим интегральное уравнение (3) и перепишем его в виде

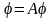. (6)

в) Последовательность непрерывных функций 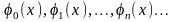, (7) заданных на отрезке будет сходиться равномерно, если

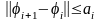, (8) причем 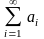-сходящийся ряд .

Сущность метода последовательных приближений (метод Пикара).

Строится последовательность функций , все эти функции непрерывны и определены на , точка . Каждая функция (7) определяется через предыдущую

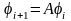, i=0,1,… (9)

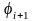Если график функции , то функция определяется по формуле (9) . Для того чтобы могла быть определена функция нужно чтобы график функции . Это требование можно выполнить, выбрав достаточно малым. За счет уменьшения длины можно добиться того, чтобы для последовательности (7) выполнялось соотношение:

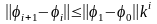, где . (10) Тогда , то есть функциональная последовательность (7) будет равномерно сходиться, и её предел будет удовлетворять соотношению (5).