2.Уравнения с разделяющимися переменными

Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида (3.1)

или уравнение вида (3.2)

Для того, чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделенными переменными, произвести следующие действия:

;

Теперь надо решить уравнение g(y)= 0. Если оно имеет вещественное решение y=a, то y=a тоже будет решением уравнения (3.1).

Уравнение (3.2) приводится к уравнению с разделенными переменными делением на произведение :

, что позволяет получить общий интеграл уравнения (3.2): 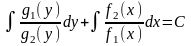. (3.3)

Интегральные кривые (3.3) будут дополнены решениями , если такие решения существуют.

Уравнения, приводящиеся к уравнениям с разделяющимися переменными. Многие дифференциальные уравнения путем замены переменной могут быть приведены к уравнениям с разделяющимися переменными. Уравнение вида   , (6)

где   и   - постоянные, приводится к уравнению с разделяющимися переменными, если ввести новую неизвестную функцию  . Тогда

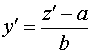  ,  , получим

  ,

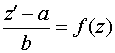   - уравнение с разделяющимися переменными.

3. Однородные и приводящиеся к ним уравнения.

Определение 1. Уравнение 1-го порядка называется однородным, если для его правой части при любых справедливо соотношение , называемое условием однородности функции двух переменных нулевого измерения. Теорема. Любая функция - однородна и, наоборот, любая однородная функция нулевого измерения приводится к виду . Доказательство. Первое утверждение теоремы очевидно, т.к. . Докажем второе утверждение. Положим 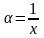, тогда для однородной функции , что и требовалось доказать.

Определение 2. Уравнение (4.1)

в котором M и N – однородные функции одной и той же степени, т.е. обладают свойством при всех , называется однородным.

Очевидно, что это уравнение всегда может быть приведено к виду (4.2) , хотя для его решения можно этого и не делать.

Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле y=zx, где z(x) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: или или .

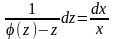Интегрируя, получаем общий интеграл уравнения относительно функции z(x) , который после повторной замены дает общий интеграл исходного уравнения. Кроме того, если - корни уравнения , то функции 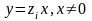- решения однородного заданного уравнения. Если же 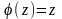, то уравнение (4.2) принимает вид

и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые: .

Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку x=zy.

Дифференциальные уравнения, приводящиеся к однородным.

4. Линейные и приводящиеся к ним уравнения.

Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид: , (7.1) где P(x) и Q(x) – заданные непрерывные функции от x. Если функция , то уравнение (7.1) имеет вид: 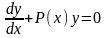(7.2) и называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением.

Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными: (7.3)

Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(x) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(x) так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:

.

Подставляя найденную производную в уравнение (7.1), будем иметь:

или .

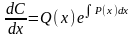Откуда , где 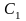- произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет (7.4)

Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при . Этот важный вывод выделим в виде теоремы.

Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения 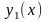, то все остальные решения имеют вид , где - общее решение соответствующего линейного однородного дифференциального уравнения.

Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде 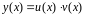. Тогда 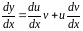. Подставим найденную производную в исходное уравнение: .

Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) за скобку: (7.5) Потребуем обращения в нуль круглой скобки: .

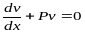Решим это уравнение, полагая произвольную постоянную C равной нулю: . С найденной функцией v(x) вернемся в уравнение (7.5): .

Решая его, получим: .

Следовательно, общее решение уравнения (7.1) имеет вид:

Уравнение Бернулли. Определение. Уравнением Бернулли называется уравнение вида , (1) где n – любое число, не обязательно целое. При уравнение Бернулли превращается в линейное неоднородное уравнение. При n=1 оно превращается в линейное однородное уравнение. Таким образом, уравнение Бернулли служит некоторым обобщением линейных уравнений, в общем случае оно является нелинейным дифференциальным уравнением (при и ). Однако во всех случаях его решение тесно связано с решением линейного уравнения. Теорема. Пусть и . Тогда уравнение Бернулли (1) подстановкою сводится к решению линейного уравнения (для функции z). Замечание. Уравнение Бернулли (1) может быть решено другим способом. Введем вместо неизвестной функции две неизвестные функции и , такие, что . (7)

Подставляя это в уравнение (1), получим:

(8)

Из этого одного уравнения определить две функции u и v нельзя. Для того, чтобы определить конкретные функции и , необходимо задать еще одну зависимость между и , причем вообще говоря, произвольную.

Но проще всего положить . (9)

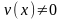Тогда уравнение (8) примет вид: или, считая (или, что то же, ) . (10)

Так как есть решение однородного линейного уравнения (9), то его можно считать его известным: . (11)

Здесь, при интегрировании уравнения (8), мы положили произвольную постоянную . Это можно делать, так как за функцию мы можем взять любое решение уравнения (9).

Итак, известно. Отсюда следует, что уравнение (10) для определения будет с разделяющимися переменными (считаем ). (12)

Отсюда получаем : или (13)

Формулы (11) и (13) позволяют построить решение уравнения Бернулли

.

Такой способ решения годится и для и n=1. В этом случае только формула (13) будет иметь другой вид, именно: 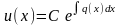, где С – произвольная постоянная.