Математичне очікування та коваріація цінних паперів

Математичне очікування		Коваріація
i	mi	Vij	І	ІІ	ІІІ
І	11	І	8	1	– 2
ІІ	5	ІІ	1	2	– 1
ІІІ	3	ІІІ	– 2	– 1	1

Необхідно: знайти структуру оптимального портфеля та відповідний ризик за умови очікуваної ефективності портфеля m_p = 6 %; визначити оптимальну структуру ризикової частини портфеля за умови наявності безризикових цінних паперів з ефективністю 2 %; визначити його ефективність і ризик.

Розв’язання

Визначимо структуру оптимального портфеля та відповідний ризик за умови значення очікуваної ефективності портфеля m_p = 6 %

;

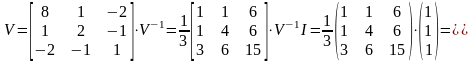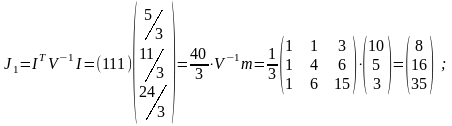
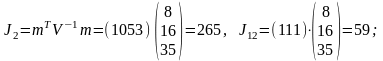
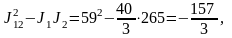
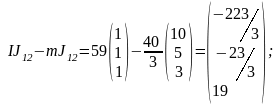
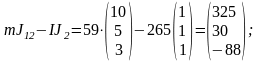
Звідси .

Таким чином, оптимальним вкладенням буде такий їх розподіл між активами: І — 37,6 %; ІІ — 18,5 %; ІІІ — 43,9 %.

При цьому

.

Знайдемо оптимальну структуру ризикової частини портфеля за умови наявності безризикових цінних паперів з ефективністю 2 %; визначимо його ефективність і ризик

;

.

; .

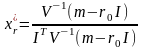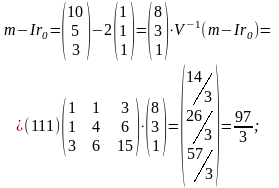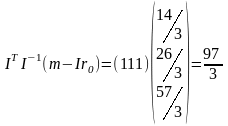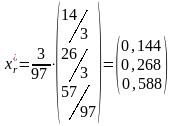Отже, структура ризикової частини портфеля така: І — 14,45 %; ІІ — 26,8 %; ІІІ — 58,8 %.

При цьому ;

;

.

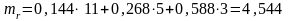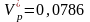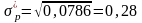Висновок: оптимальна структура портфеля за умови очікуваної ефективності портфеля m_p = 6 % становить: І — 37,6 %; ІІ — 18,5 %; ІІІ — 43,9 %, ризик — 84,2 %.

Оптимальна структура ризикової частини портфеля за умови наявності безризикових цінних паперів з ефективністю 2 %: І — 14,45 %; ІІ — 26,8 %; ІІІ — 58,8 %, ризик — 28,2 %.

Приклад 7.1

Адміністрація театру вирішує, скільки потрібно замовити програмок для вистав. Вартість замовлення — 200 грн плюс 0,3 грн за штуку. Програмки продаються за 0,6 грн за штуку, і до того ж дохід від реклами становить додатково 300 грн. Із минулого досвіду відомо відвідування театру (табл. 1).

Таблиця 1

Відвідування театру

Відвідування, осіб	4000	4500	5000	5500	6000
Імовірність	0,1	0,3	0,3	0,2	0,1

Припускається, що 40 % відвідувачів купують програмки. Потрібно побудувати платіжну матрицю доходів і визначити, яку кількість продукції театру необхідно замовити за допомогою таких критеріїв, як: математичне сподівання, дисперсія, середньоквадратичне відхилення та коефіцієнт варіації. За іншими критеріями ПР в умовах ризику розв’язок прикладу наведено в розділі 5.

Розв’язання

Побудуємо платіжну матрицю прибутків (табл. 2).

Таблиця 2

Матриця прибутків, тис. Грн

Пропозиція програмок (40 % відвідувачів), Аi	Попит на програмки, Sj
	1600	1800	2000	2200	2400
4000 · 0,4 = 1600	(1600 · 0,6 + 300) – – (1600· 0,3 + 200) = 580	580	580	580	580
4500 · 0,4 = 1800	(1600 · 0,6 + 300) – – (1800 · 0,3 + 200) = 520	(1800 · 0,6 + 300) – – (1800 · 0,3 + 200) = 640	640	640	640
5000 · 0,4 = 2000	460	580	700	700	700
5500 · 0,4 = 2200	400	520	640	760	760
6000 · 0,4 = 2400	340	460	580	700	820
Імовірність	0,1	0,3	0,3	0,2	0,1

Розрахуємо показники кількісної оцінки ризиків: математичне сподівання, дисперсію, середньоквадратичне відхилення та ко- ефіцієнт варіації (табл. 3).

Висновок: найбільший імовірний прибуток можливо отримати за умови замовлення 2000 програмок. Найменше відхилення від очікуваного результату та найменший ризик (0 %) має перший варіант (А₂), згідно з яким адміністрації театру необхідно замовляти 1600 штук програмок. Порівнюючи значення ймовірних прибутків та ступеня ризику доцільно обрати другий варіант, який передбачає замовлення 1800 програмок. За А₂ ризик неотримання очікуваного прибутку в розмірі 628 тис. грн становить 5,7 %.