Вибір оптимального рішення за критерієм вальда
Варіант рішення |
Варіанти станів середовища |
mіnj{V(Ai, Sj)} |
maxi mіnj{V(Ai, Sj)} |
||
S1 |
S2 |
S3 |
|||
А1 |
2,5 |
3,5 |
4,0 |
2,5 |
А1 |
А2 |
1,5 |
2,0 |
3,5 |
1,5 |
|
А3 |
3,0 |
8,0 |
2,5 |
2,5 |
А3 |
А4 |
7,5 |
1,5 |
3,5 |
1,5 |
|
За критерієм Вальда оптимальними будуть альтернативні рішення А1 і А3, які вважаються еквівалентними, тобто мають однакові переваги для виконання.
Для того щоб застосувати критерій Севіджа, потрібно побудувати матрицю ризику як лінійне перетворення функціоналу оцінювання.
Для побудови матриці ризику використаємо такі формули:
для
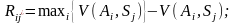(8)
для
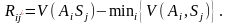(9)
Матрицю ризику побудуємо в табл. 6.
Таблиця 6
Побудова матриці ризику
Варіант рішення |
Матриця прибутків (V(Ai, Sj)) |
Матриця ризику (Rij) |
|||||
Варіанти станів середовища |
Варіанти станів середовища |
||||||
S1 |
S2 |
S3 |
S1 |
S2 |
S3 |
||
А1 |
2,5 |
3,5 |
4,0 |
7,5 – 2,5 = 5,0 |
8,0 – 3,5 = 4,5 |
4,0 – 4,0 = 0 |
|
А2 |
1,5 |
2,0 |
3,5 |
7,5 – 1,5 = 6,0 |
8,0 – 2,0 = 6,0 |
4,0 – 3,5 = 0,5 |
|
А3 |
3,0 |
8,0 |
2,5 |
7,5 – 3,0 = 4,5 |
8,0 – 8,0 = 0 |
4,0 – 2,5 = 1,5 |
|
А4 |
7,5 |
1,5 |
3,5 |
7,5 – 7,5 = 0 |
8,0 – 1,5 = 6,5 |
4,0 – 3,5 = 0,5 |
|
Тепер можна застосувати критерій Севіджа до матриці ризику за формулою:
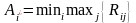. (10)
Таблиця 7
Вибір оптимального рішення за критерієм Севіджа
Варіант рішення |
Варіант стану середовища |
maxj{Rij} |
mini maxj{Rij} |
||
S1 |
S2 |
S3 |
|||
А1 |
5,0 |
4,5 |
0 |
5,0 |
|
А2 |
6,0 |
6,0 |
0,5 |
6,0 |
|
А3 |
4,5 |
0 |
1,5 |
4,5 |
А3 |
А4 |
0 |
6,5 |
0,5 |
6,5 |
|
За критерієм Севіджа оптимальним буде альтернативне рішення А3 (табл. 7).
За допомогою критерію Гурвіца встановимо баланс між випадками крайнього оптимізму ат випадками крайнього песимізму за допомогою коефіцієнта оптимізму . Цей коефіцієнт визначається від нуля до одиниці та показує ступінь схильностей особи, що приймає рішення, до оптимізму чи песимізму. Якщо = 1, то це свідчить про крайній оптимізм, якщо = 0 — крайній песимізм. За умов задачі = 0,6.
Оптимальну альтернативу за критерієм Гурвіца знаходимо за формулами:
для
. (5.11)
для
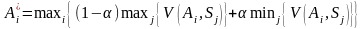. (5.12)
Оптимальним рішенням за критерієм Гурвіца буде альтернативне рішення А3 (табл. 8).
Таблиця 8
Вибір оптимального рішення за критерієм Гурвіца
Варіант рішення |
Варіант стану середовища |
maxj {V(Ai, Sj)} |
minj {V(Ai, Sj)} |
· maxj{V(Ai, Sj)} + + (1 – )minj{V(Ai, Sj)} |
maxi{ · maxj{V (Ai, Sj)} + (1 – ) × × minj{V(Ai, Sj)}} |
||||||
S1 |
S2 |
S3 |
|||||||||
А1 |
2,5 |
3,5 |
4,0 |
4,0 |
2,5 |
4,0 · 0,6 + 2,5 · 0,4 = 3,4 |
|
||||
А2 |
1,5 |
2,0 |
3,5 |
3,5 |
1,5 |
3,5 · 0,6 + 1,5 · 0,4 = 2,7 |
|
||||
А3 |
3,0 |
8,0 |
2,5 |
8,0 |
2,5 |
8,0 · 0,6 + 2,5 · 0,4 = 5,8 |
А3 |
||||
А4 |
7,5 |
1,5 |
3,5 |
7,5 |
1,5 |
7,5 · 0,6 + 1,5 · 0,4 = 5,1 |
|
||||
Висновок: розрахунок за всіма даними критеріями довів доцільність виробництва продукції за альтернативним варіантом А3.
Приклад 5.2 |
Дано платіжну матрицю (табл. 1). Спростити матрицю за рахунок відбраковування явно невигідних стратегій [31].
Таблиця 1