Розв’язання

Оптимальну альтернативу за критерієм Байєса знаходимо за формулами:

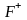
для ; (1)

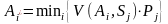для . (2)

Ми знаходимо оптимальну альтернативу випуску продукції з погляду максимізації прибутків, тобто функціонал оцінювання має позитивний інгредієнт — F⁺, і будемо використовувати відповідні формули (розрахунки подано в табл. 2).

Таблиця 2

Вибір оптимального рішення за критерієм Байєса

Варіант рішення	Варіанти станів середовища			V(Ai, Sj) · Pj	maxi{V(Ai, Sj) · Pj}
	S1	S2	S3
А1	2,5	3,5	4,0	2,5 · 0,25 + 3,5 · 0,55 + 4,0 · 0,2 = 3,35
А2	1,5	2,0	3,5	1,5 · 0,25 + 2,0 · 0,55 + 3,5 · 0,2 = 2,18
А3	3,0	8,0	2,5	3,0 · 0,25 + 8,0 · 0,55 + 2,5 · 0,2 = 5,65	А3
А4	7,5	1,5	3,5	7,5 · 0,25 + 1,5 · 0,55 + 3,5 · 0,2 = 3,40

За критерієм Байєса оптимальним буде альтернативне рішення А3.

Критерій Лапласа характеризується невідомим розподілом імовірностей на множині станів середовища та базується на принципі «недостатнього обґрунтування», який означає: коли немає даних для того, щоби вважати один зі станів середовища більш імовірним, то ймовірності станів середовища треба вважати рівними. Оптимальну альтернативу за критерієм Лапласа знаходимо за формулами:

для 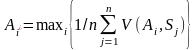; (3)

для . (4)

Таблиця 3

Вибір оптимального рішення за критерієм Лапласа

Варіант рішення	Варіант стану середовища					maxi{1/nV(Ai, Sj)}
	S1	S2	S3
A1	2,5	3,5	4,0		1/3 · (2,5 + 3,5 + 4,0) = 3,33
A2	1,5	2,0	3,5		1/3 · (1,5 + 2,0 + 3,5) = 2,33
A3	3,0	8,0	2,5		1/3 · (3,0 + 8,0 + 2,5) = 4,50	А3
A4	7,5	1,5	3,5		1/3 · (7,5 + 1,5 + 3,5) = 4,16

За критерієм Лапласа оптимальним буде альтернативне рішення А3 (табл. 3).

За правилом максимакс альтернативу знаходимо за формулою:

. (5)

Скориставшись цим правилом, визначаємо максимальні значення для кожного рядка та вибираємо найбільше з них.

За правилом максимакс оптимальним буде альтернативне рішення А3 (табл. 4).

Таблиця 4

Вибір оптимального рішення за правилом максИмакс

Варіант рішення	Варіант стану середовища				maxj{V(Ai, Sj)}		maxi mахj{V(Ai, Sj)}
	S1	S2	S3
А1	2,5	3,5	4,0	4,0
А2	1,5	2,0	3,5	3,5
А3	3,0	8,0	2,5	8,0		А3*
А4	7,5	1,5	3,5	7,5

Критерій Вальда вважається найобережнішим із критеріїв. Оптимальне альтернативне рішення за цим критерієм знаходимо за формулами:

для 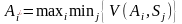; (6)

для . (7)

Таблиця 5