Граничні похибки

Стратегії, Sі	Прибуток за з/е умов					∆і
	1	2	3	4	5
S1	17	5	24	10	4	15,61
S2	11	20	14	32	46	25,53
S3	35	5	3	37	2	38,86
S4	15	14	10	30	6	13,42
S5	17	23	20	9	12	10,08
S6	19	4	16	2	1	20,43

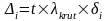, (8)

де t — критерій Стьюдента (таблична величина),  — рівень значущості, або ймовірність, з якою відхиляється рівень граничної похибки.

Додамо граничну похибку до середньої ефективності (математичного сподівання) й дістанемо максимально можливий рівень ефективності із заданою ймовірністю: . У результаті віднімання матимемо мінімально можливе значення очікуваної ефективності: 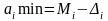. Чим менше значення граничної похибки (граничного відхилення), тим безпечніша й надійніша стратегія. Такою є п’ята стратегія.

Результати розрахунків подано в табл. 10.

Таблиця 10

Максимально та мінімально можливий рівень ефективності

Стратегії, Sі	Прибуток за з/е умов					aimax	aimin
	1	2	3	4	5
S1	17	5	24	10	4	29,59	– 1,63
S2	11	20	14	32	46	41,73	– 9,33
S3	35	5	3	37	2	65,37	– 12,35
S4	15	14	10	30	6	28,74	1,90
S5	17	23	20	9	12	27,42	7,26
S6	19	4	16	2	1	34,32	– 6,54

За табл. 10 ми можемо проаналізувати зміни граничних інтервалів ефективності стратегій:

• a_imax характеризує максимальну границю інтервалу ефективності, тобто очікувані прибутки; тут кращою є третя стратегія;

• a_imin характеризує мінімальне значення інтервалу ефективності; коли воно від’ємне, тоді ми можемо бачити розмір утрат; виходячи з цих умов вигіднішою є п’ята стратегія, завдяки своїй не збитковості та найбільшому додатному значенню.

Визначимо ризик на основі розмаху варіації:

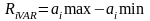. (9)

Результати розрахунків подано в табл. 11.

Чим більше розмах варіації, тим більший ризик притаманний стратегії. Отже, п’ята стратегія є найменш ризикованою.

Таблиця 11