Розв’язання

1. Визначення середньої ефективності кожної стратегії:

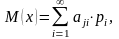(1)

де і — номер стратегії;

j — номер зовнішньоекономічної умови;

a_ij — прибуток, який може отримати фірма від і-стратегії за j-умов.

Результати розрахунків подано в табл. 2.

Таблиця 2

Ефективність стратегій

Стратегії, Sі	Прибуток за з/е умов						Мі
	1	2	3	4	5
S1	17	5	24	10	4	14
S2	11	20	14	32	46	16,2
S3	35	5	3	37	2	26,5
S4	15	14	10	30	6	15,3
S5	17	23	20	9	12	17,3
S6	19	4	16	2	1	13,9
Рі	0,64	0,18	0,05	0,08	0,05	×

Оскільки ми знаємо, що чим більша середня ефективність стратегії, тим вигідніша стратегія, то, керуючись матрицею табл. 2 прикладу 7.1, бачимо, що третя стратегія має найбільшу середню ефективність і є найвигіднішою, а решта стратегій № 1; 2; 4; 5; 6 найменш ефективні.

2. Кількісна оцінка ризикованості кожної стратегії на основі показників варіації:

а) за дисперсією:

. (2)

Результати розрахунків подано в табл. 3.

Таблиця 3

Дисперсії стратегій

Стратегії, Sі	Прибуток за з/е умов						Dі
	1	2	3	4	5
S1	17	5	24	10	4	31,62
S2	11	20	14	32	46	84,52
S3	35	5	3	37	2	195,89
S4	15	14	10	30	6	23,38
S5	17	23	20	9	12	13,18
S6	19	4	16	2	1	54,16
Рі	0,64	0,18	0,05	0,08	0,05	×

Дисперсія є одним з абсолютних показників кількісної оцінки ризику. Чим більша дисперсія, тим більший ризик притаманний стратегії. Виходячи з цього стратегія № 5 характеризується меншим ризиком, ніж решта стратегій, тобто за цим показником п’ята стратегія є вигіднішою;

б) на основі стандартного відхилення (сигма):

. (3)

Результати розрахунків подано в табл. 4

Таблиця 4