3 Порядок выполнения работы

Для решения поставленных задач введем обозначения:

Y(t)– доход в момент времени t;

С(t)– потребление в момент времени t;

I(t)– инвестиции в момент времени t.

Исходя из основного допущения модели, в котором предполагается, что скорость роста дохода пропорциональна инвестициям: , где В - коэффициент капиталоемкости прироста дохода, запишем уравнение динамики дохода, дополнив его начальным условием:

(1)

Первый вариант модели получается, если считать С(t) = 0. Хотя с практической точки зрения такой вариант не реализуем, все же он позволяет определить максимальные технически возможные темпы роста. В этом случае получаем:

(2)

(2) – задача Коши для линейного однородного дифференциального уравнения, и её решение (доказать) имеет вид:

Таблица 1 – Динамика дохода при С=0

t	Y1	C1
0	80,00	0,00
1	88,41	0,00
2	97,71	0,00
3	107,99	0,00
4	119,35	0,00
5	131,90	0,00
6	145,77	0,00
7	161,10	0,00
8	178,04	0,00
9	196,77	0,00
10	217,46	0,00

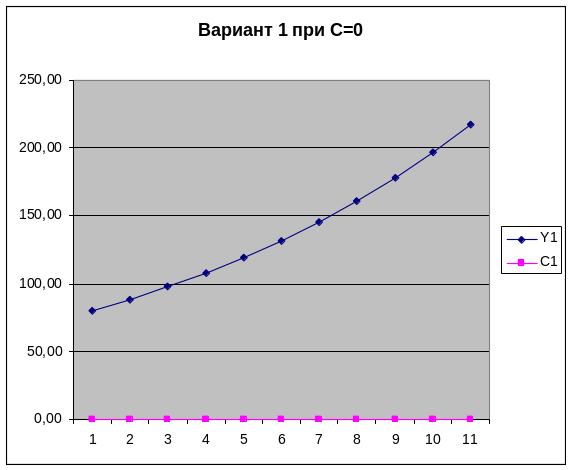
Рисунок 1 – Динамика дохода при нулевом уровне потребления

Непрерывный темп прироста здесь равен = 1/В, что соответствует максимально технологически возможному темпу прироста.

Рассмотрим второй вариант, С(t) = С постоянно во времени. Исходя из базовой модели Харрода-Домара (1), получаем неоднородное линейное дифференциальное уравнение

Решение (доказать самостоятельно) имеет вид

.

Непрерывный темп прироста дохода [ ] в этом варианте равен . В начальный момент времени (при t=0) он составляет и, возрастая при t→∞, стремится к 1/B. То есть доход растет, а постоянный объем потребления составляет все меньшую его долю. Величина в скобках есть норма накопления в момент времени t; темп прироста дохода пропорционален этой величине, как и показателю приростной капиталоотдачи 1/B.

Таблица 1 – Динамика дохода при С=const

t	Y2	C2
0	80,00	60,00
1	82,10	60,00
2	84,43	60,00
3	87,00	60,00
4	89,84	60,00
5	92,97	60,00
6	96,44	60,00
7	100,28	60,00
8	104,51	60,00
9	109,19	60,00
10	114,37	60,00

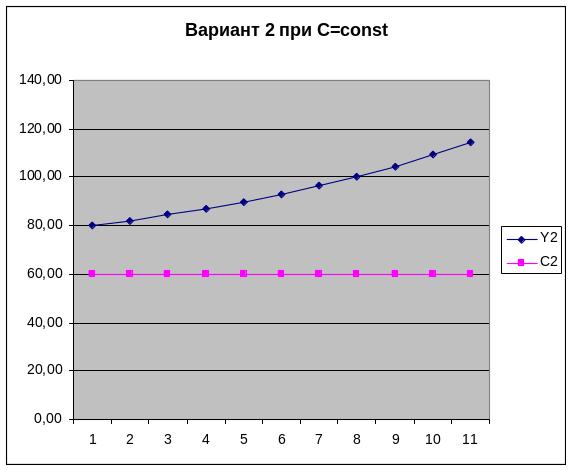
Рисунок 2 – Динамика дохода при постоянном уровне потребления

Следовательно, при прочих равных условиях рост нормы накопления пропорционально увеличивает темпы прироста дохода. В то же время это снижает уровень текущего потребления, и возникает проблема согласования конкурентных целей увеличения темпов роста и уровня текущего благосостояния.

Рассмотрим третий вариант модели с показателем потребления С(t), растущим с постоянным темпом r:

Модель примет вид:

Решение поставленной задачи (проверить самостоятельно) имеет вид:

(**)

Далее рассмотрим, как влияет на характер решения величина r.

1 случай. Предположим, что r>1/В, тогда потребление будет занимать все большую и в конце концов - подавляющую часть дохода, что сведет к нулю сначала инвестиции, а затем и доход. Ясно это и из формулы решения модели, поскольку в случае r>1/B коэффициент 1/(1-Br) отрицателен, а е^rt растет быстрее, чем е ^(1/B)t, - следовательно, второе слагаемое при этом отрицательно и через некоторое время «перевесит» первое.

Таблица 1 – Динамика дохода при

t	Y31	C31
0	80,00	60,00
1	81,44	73,28
2	81,49	89,51
3	79,65	109,33
4	75,32	133,53
5	67,72	163,10
6	55,89	199,21
7	38,61	243,31
8	14,39	297,18
9	-18,63	362,98
10	-62,78	443,34

Рисунок 3 – Динамика дохода при темпе прироста потребления r1= 0,4 (> 1/B).

Из графика видно, что с течением времени потребление будет занимать все большую и, в конце концов, – подавляющую часть дохода. В результате инвестиции придут к нулевой отметке, а затем и доход. Данная модель не может рассматриваться как оптимальная, поскольку в экономике появляется ситуация накопления ради потребления.

2 случай. Если в рассматриваемой модели роста 1/B>r> ₀/B, то требуемый темп прироста потребления оказывается слишком высоким для экономики. В этом случае коэффициент отрицателен и, поскольку 1/B>r, первое, отрицательное слагаемое в решении «перевешивает» в конце концов, второе. Поэтому темп прироста дохода падает и становится с некоторого момента отрицательным. Через некоторое время сам доход становится равным нулю, после чего модель теряет экономический смысл. В данном случае слишком низкой оказывается начальная норма накопления ₀.

Таблица 4 – Динамика дохода при

t	Y32	C32
0	80,00	60,00
1	80,26	98,92
2	75,26	163,10
3	61,01	268,90
4	30,89	443,34
5	-26,11	730,95
6	-128,18	1205,13
7	-305,43	1986,93
8	-607,55	3275,89
9	-1116,59	5401,03
10	-1967,96	8904,79

Рисунок 4 – Динамика дохода при темпе прироста потребления, r2 = 0,3 (1/B>r> 0/B).

3 случай. Если r < ₀/B, то норма накопления, а вместе с ней и темп прироста дохода растут, причем последний в пределе приближается к 1/B. Однако в этом случае происходит “накопление ради накопления”, ибо потребление растет заданным темпом r, а темп прироста дохода удается увеличить за счет более быстрого роста инвестиций. Норма накопления ₀ здесь превышает Вr, и если исходить из задачи максимизации объема потребления, то эта норма слишком высока. Более высокий ее уровень требует увеличения инвестиций I(0) за счет сокращения потребления С(0) в начальный момент, что при фиксированном темпе прироста потребления r обусловливает более низкий его уровень на всей траектории.

Рисунок 5 – Динамика дохода и потребления при темпе прироста потребления, r3. = 0,05

4 случай. Предположим, что , тогда из (6) остается, что (7) - данное соотношение называется моделью Харрода.

Рисунок 6 – Динамика дохода при темпе прироста потребления, r4 = 0,333 (r= 0/B).

Следовательно нужный темп прироста потребления при r < 1/B можно поддерживать, как видно из графика, при ₀ = Вr. Таким образом, если требуется поддерживать постоянный темп прироста потребления r, не превышающий технологического темпа, то для максимизации объема потребления за любой период нужно установить начальную норму накопления ₀ = Вr.

Если r = р₀, то темп прироста дохода равен темпу прироста потребления, и решением является . Норма накопления (t)в этом случае постоянна во времени и равна ₀, а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоемкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.

Более сложен вопрос о том, какой уровень темпа r более предпочтителен. Большая его величина позволяет обеспечить больший объем потребления за длительный период, но это происходит за счет сокращения потребления на начальном этапе. Таким образом, для выбора значения r (если оно предполагается постоянным) нужна информация о межвременных предпочтениях лица, принимающего решение.

Для того, чтобы не происходило накопления ради накопления, целесообразно выбирать темпы прироста потребления на уровне ρ₀/В, т.е. в нашем случае на уровне 0,08333. В этой модели темп прироста дохода равен темпу прироста потребления. Темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоемкости.

Из анализа всех построенных моделей можно сделать вывод, что первая модель развития экономики при темпе прироста потребления r1= 0,4 (> 1/B) не может рассматриваться как оптимальная, поскольку в экономике появляется ситуация накопления ради потребления. Во второй модели при темпе прироста потребления r2=0,3 (1/B>r>a0) наблюдается ситуация, в которой темп прироста дохода падает и становится с момента времени t=4,5 отрицательной величиной. В результате сам доход становится равным нулю, модель теряет экономический смысл. Наиболее оптимальным вариантом развития экономики является модель (рис.9), с темпом роста потребления /В=0,08333 и нормой накопления в данном случае постоянной во времени ₀=0,25, поскольку темп прироста дохода равен темпу прироста потребления. Темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоемкости.