8. Наиболее важными методами интегрирования являются: 1) метод непосредственного интегрирования (метод разложения), 2) метод подстановки (метод введения новой переменной), 3) метод интегрирования по частям.
I. Метод непосредственного интегрирования
Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.
II. Метод подстановки (интегрирование заменой переменной)
Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле
∫f(x)dx=∫f(φ(t))φ'(t)dt
Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной.
III. Метод интегрирования по частям
Метод интегрирование по частям основан на следующей формуле:
∫udv=uv-∫vdu
где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.
9. Пусть на отрезке [ab] дана непрерывная функция y=f(x). Необходимо найти площадь криволинейной трапеции (криволинейная трапеция- часть плоскости, заключенная между графиком функции, осью ОХ и вертикальными прямыми х=а и х=b)
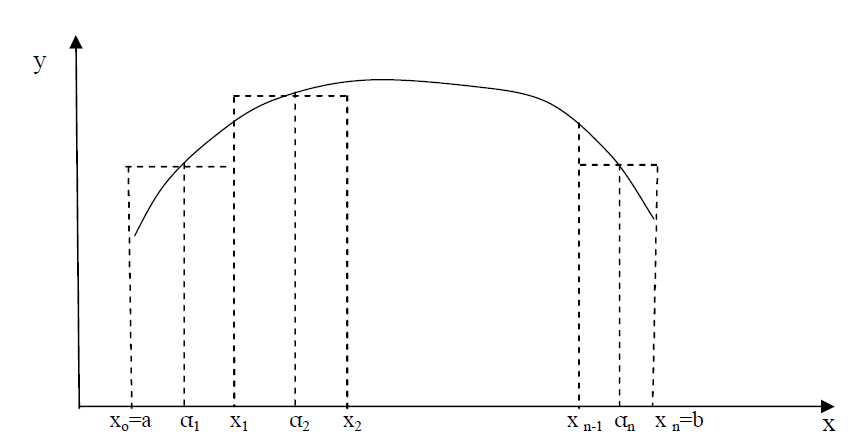
Разобьем отрезок [ab] на n отрезков точками xo=a , x1 , x2 …….. x n=b . Длина каждого из отрезков будет равна: Δx= xo- x1,….,Δxn= xn- xn-1. Внутри каждого отрезка разбиения возьмем точки α1, α2…..αn и вычислим значения функции в этих точках: f(α1), f(α2),….., f(αn). Составим сумму площадей полученных прямоугольников:
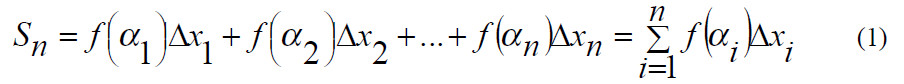
Сумма (1) называется интегральной суммой функции y=f(x) на отрезке [a,b] и
представляет собой сумму площадей всех прямоугольников и, следовательно,
приближенно выражает площадь криволинейной трапеции, и тем точнее, чем больше число участков разбиения и чем меньше длина каждого из них.
Опр. 1 Определенным интегралом от функции y=f(x) на отрезке [a,b] называется предел интегральной суммы (1), когда число участков разбиения стремится к бесконечности, а длина каждого из них стремится к нулю:
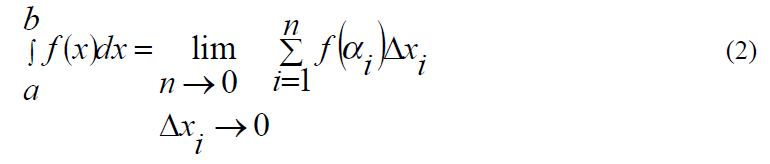
Где a и b называются пределами интегрирования, причем а – нижний предел
интегрирования, а b – верхний предел интегрирования. Геометрический смысл неопределенного интеграла - площадь криволинейной трапеции.
10.
11. Основные понятия об обыкновенных дифференциальных уравнения (оду)
Дифференциальное уравнение - это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значения её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные.
Все дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения(ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Порядком или степенью дифференциального уравнения называется наибольший порядок производных, входящих в дифференциальное уравнение.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени. Формулировка второго закона Ньютона для материальной точки дает простейший пример обыкновенного дифференциального уравнения второго порядка с неизвестной функцией координат точки и временем, выступающим в роли независимой переменной.
Обыкновенное
дифференциальное уравнение
(ОДУ)
-ого
порядка — это уравнение вида
где
—
неизвестная функция (возможно,
вектор-функция; в таком случае часто
говорят о системе
дифференциальных уравнений),
зависящая от независимой переменной
,
штрих означает дифференцирование
по
.
Решением
дифференциального уравнения
называется
раз
дифференцируемая
функция
,
удовлетворяющая уравнению во всех
точках своей области определения. Обычно
существует целое множество таких функций
(такое параметризованное семейство
рещений называется общим
решением дифференциального уравнения),
и для выбора одного из них требуется
наложить на него дополнительные условие:
например, потребовать, чтобы решение
принимало в данной точке данное значение.
Полученное единственное решение
называется частным решением. Общее
решение обыкновенного дифференциального
уравнения
-ого
порядка может быть выражено в виде
где
,
-
произвольные постоянные. Если общее
решение задано в неявном виде выражением
то это выражение называют общим интегралом дифференциального уравнения.
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение вида
или
называется дифференциальным уравнением с разделяющимися переменными.
Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.
Для
решения такого дифференциального
уравнения
необходимо домножить или разделить обе
части дифференциального
уравнения на
такое выражение, чтобы в одну часть
уравнения входили только функции от
и
,
в другую часть уравнения - только функции
от
,
.
Затем в полученном дифференциальном
уравнении надо
проинтегрировать обе части:
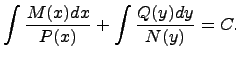
12.
ОСНОВНЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Основные
определения и термины
Возникновение
отказов в информационных системах
зависит от разных факторов и носит
случайный характер. Поэтому для
количественной оценки различных
характеристик систем используются
вероятностные методы.
В теории
вероятностей случайной называется
величина, которая в результате опыта
может принять то или иное значение,
предугадать которое заранее и достоверно
невозможно.
Событием в теории
вероятностей считается всякий факт,
который в результате опыта может
произойти, а может и не произойти.
Для
количественного сравнения между собой
событий по степени их возможности
используется определенное число, которое
тем больше, чем более возможно событие.
Такое число называется вероятностью
события.
В практике о вероятности
события судят по частоте его появления.
Если
в n
опытах событие А появилось m
раз, то его частота или статистическая
вероятность может быть определена
соотношением
.
Невозможным
называется событие, которое заведомо
не произойдет. Вероятность невозможного
события равна нулю.
Достоверным
называется событие, которое обязательно
произойдет. Вероятность достоверного
события равна единице.
Вероятность
произвольного случайного события
изменяется от нуля до единицы.
Если
случайное событие имеет очень малую
вероятность, то практически можно
считать, что в единичном опыте это
событие не наступит. Очень малая
вероятность – это значения, заключенные
между 0,01 и 0,05. Это свойство называется
принципом практической невозможности
маловероятных событий.
При
неограниченном увеличении числа опытов
статистическая вероятность сходится
по вероятности к математической, т. е.
частота с вероятностью сколь угодно
близкой к единице, приближается к
математической вероятности Р(А).
Если
исходы (результаты) испытаний единственно
возможны и равновозможны, математическая
вероятность события А может быть
вычислена по формуле:
,
где
n
– общее число равновозможных элементарных
исходов испытаний;
m
– число благоприятных исходов, в которых
появляется событие А.
При вычислении
величин m
и n
используется теория сочетаний.
Число
сочетаний из m
элементов по n
вычисляется по любой из двух
формул:
,
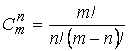(2.1)
.
(2.2)