
- •Вектор алгебрасы Векторлар өстендә сызыкча гамәлләр башкару.
- •Векторның озынлыгы. Юнәлтүче косинуслар. Ноктаның координаталары. Нокталар арасындагы ераклык.
- •Векторларның скаляр тапкырчыгышы.
- •Векторларның вектор тапкырчыгышы.
- •Векторларның катнаш тапкырчыгышы.
- •14. Векторларны скаляр тапкырлау.
- •15. Векторларның вектор тапкырчыгышы.
- •16. Векторларның катнаш тапкырчыгышы.
Векторларның катнаш тапкырчыгышы.
Векторларның катнаш
тапкырчыгышы дип
һәм
векторларын
векторча тапкырлап килеп чыккан векторны,
![]() векторына
скалярча тапкырлаганга тигез булган
сан
атала:
векторына
скалярча тапкырлаганга тигез булган
сан
атала:![]() .
Геометрик мәгънәсе:
векторларның катнаш
тапкырчыгышы
,
һәм
векторларыннан
төзелгән параллелепипед
күләменә тигез була :
.
Геометрик мәгънәсе:
векторларның катнаш
тапкырчыгышы
,
һәм
векторларыннан
төзелгән параллелепипед
күләменә тигез була :
![]() .
.
Векторларның катнаш тапкырчыгышының үзлекләре:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() һәм
һәм
![]() -компланар
-компланар
![]() ;
;
Координаталары белән
бирелгән
,
һәм
![]() векторлары өчен катнаш тапкырчыгыш
түбәндәге формула ярдәмендә исәпләнә:
векторлары өчен катнаш тапкырчыгыш
түбәндәге формула ярдәмендә исәпләнә:
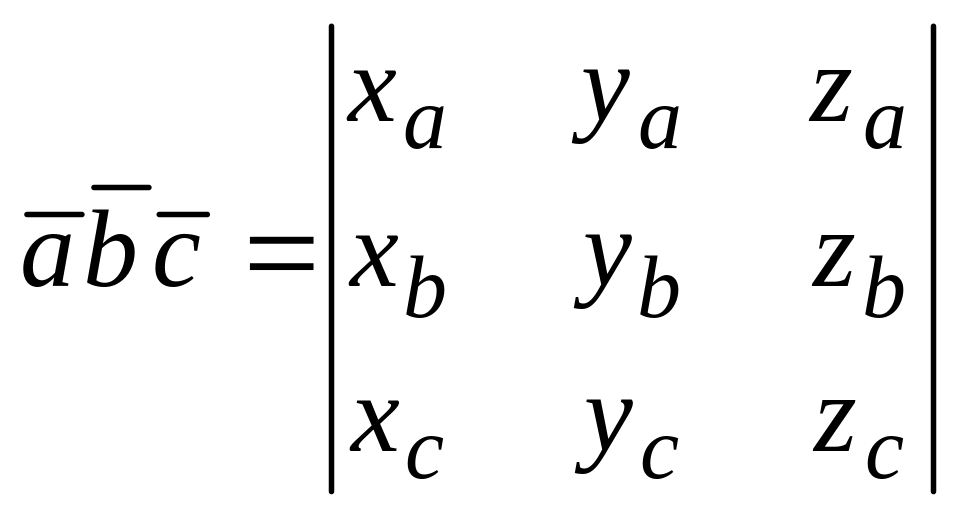 .
.
Векторларның катнаш тапкырчыгышының кайбер өстәмәләре:
1) Кабыргалары
,
һәм
![]() векторларында
яткан тетраэдр һәм параллелепипед
күләмнәре түбәндәге формула ярдәмендә
исепләнә:
векторларында
яткан тетраэдр һәм параллелепипед
күләмнәре түбәндәге формула ярдәмендә
исепләнә:
![]() .
.
2) Фәзадагы
векторларның ориентациясен билгеләү:
![]() –уң;
–уң;
![]() –сул.
–сул.
3) Векторларның компланарлык шарты :
![]() һәм
-
компланар.
һәм
-
компланар.
4)
![]() ноталарының
бер яссылыкта ятуларын билгеләү:
ноталарының
бер яссылыкта ятуларын билгеләү:
![]()
Мисал 1.
![]() ,
,
![]() ,
,
![]() векторының компланар
булуларын күрсәтергә.
векторының компланар
булуларын күрсәтергә.
Чишү.
,
,
![]() векторларының
катнаш тапкырчыгышын табабыз:
векторларының
катнаш тапкырчыгышын табабыз:

![]() .
.
![]() ,
димәк, бирелгән векторлар компланар.
,
димәк, бирелгән векторлар компланар.
Җавап: , , - компланар.
Мисал 2.
Түбәләре
![]() ,
,
![]() ,
,
![]() ,
,
![]() булган тетраэдрның күләмен
табарга.
булган тетраэдрның күләмен
табарга.
Чишү.
![]() ,
,
,
,
![]() векторларын,
ягъни тетраэдрның
кабыргаларын табабыз:
векторларын,
ягъни тетраэдрның
кабыргаларын табабыз:
![]() ,
,
![]() ,
,
![]() .
.
Табылган векторларның катнаш тапкырчыгышын исәплибез:

![]() .
.
Димәк,
![]() .
.
Җавап:
![]() (күләм
берәмлеге)
(күләм
берәмлеге)
2.88
![]() векторлары уң һәм алар үзара
перпендикуляр:
векторлары уң һәм алар үзара
перпендикуляр:
![]() Исәпләргә:
Исәпләргә:
![]() .
.
2.89
![]() векторлары – сул. Әгәр
векторлары – сул. Әгәр
![]() булса,
табарга:
.
булса,
табарга:
.
2.90
![]() векторларының
ориентациясен билгеләргә:
векторларының
ориентациясен билгеләргә:
а)![]() ;
б)
;
б)![]() .
.
2.91 Бердәйлекләрне исбатларга:
а)![]()
б)![]()
2.92 Әгәр
![]() булса,
тпакырчыгышларны исәпләргә:
булса,
тпакырчыгышларны исәпләргә:
а)![]() б)
б)
![]() .
.
2.93 Векторларның компланарлыгын тикшерергә:
a)
![]() ;
;
б)
![]()
2.94
![]() нинди кыйммәтләр алганда
векторлары
компланар булачак?
нинди кыйммәтләр алганда
векторлары
компланар булачак?
а)
![]()
б)
![]()
2.95
![]() векторлары,
барлык векторлар күплегендә, базисны
тәкил итүне тикшерергә :
векторлары,
барлык векторлар күплегендә, базисны
тәкил итүне тикшерергә :
a)
![]() ;
;
б)
![]()
2.96 Нокталар бер яссылыкта яталармы?
а)
![]() ,
B(1,2,1), C(2,3,0),
,
B(1,2,1), C(2,3,0),
![]() ;
;
б) A(7,0,3),
![]() ,
,
![]() ,
,
![]() .
.
2.97 Әгәр
![]() ,
,
![]() ,
,
![]() булса,
тетраэдрының
күләмен исәпләргә.
булса,
тетраэдрының
күләмен исәпләргә.
2.98 Тетраэдрының
күләмене 5;
![]() ,
B(3,0,1),
,
B(3,0,1),
![]() –
аның түбәләре. Ординаталар күчәрендә
ятучы D түбәсенең
координаталарын табарга.
–
аның түбәләре. Ординаталар күчәрендә
ятучы D түбәсенең
координаталарын табарга.
2.99
тетраэдрының түбәләре:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() биеклегенең
озынлыгын табарга..
биеклегенең
озынлыгын табарга..
2.100
![]() векторларында
төзелгән параллелепипед
биеклеген табарга. Нигез итеп
векторларында
төзелгән параллелепипед
биеклеген табарга. Нигез итеп
![]() һәм
һәм
![]() векторларында
төзелгән параллелограммны
алырга
векторларында
төзелгән параллелограммны
алырга
2.101 Өчпочмаклы
![]() призмасында
призмасында
![]() һәм
һәм
![]() векторлары нигезне билгелиләр, ә
векторлары нигезне билгелиләр, ә
![]() векторы ян кабырга буенча юнәлгән.
Призманың күләмен һәм бииеклеген
табарга.
векторы ян кабырга буенча юнәлгән.
Призманың күләмен һәм бииеклеген
табарга.
2.102
![]()
![]() компланар
булмаган векторлар бирелгән.
компланар
булмаган векторлар бирелгән.
![]() векторының
озынлыгын табарга, биредә Н
- О ноктасының АВС
яссылыгына ортогональ
проекциясе.
векторының
озынлыгын табарга, биредә Н
- О ноктасының АВС
яссылыгына ортогональ
проекциясе.
Вектор алгебрасы буенча мөстәкыйль эш вариантлары.
14. Векторларны скаляр тапкырлау.
14.1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() нокталары бирелгән. Табарга
нокталары бирелгән. Табарга
![]() .
.
14.2.
![]() векторы
векторы
![]() һәм
һәм
![]() векторларына
перпендикуляр һәм
векторларына
перпендикуляр һәм
![]() шартын канәгатьләндерә.
векторының
координаталарын табарга.
шартын канәгатьләндерә.
векторының
координаталарын табарга.
14.3. Түбәләре![]() ,
,
![]() ,
,
![]() ,
,
![]() нокталарында булган дүрткырлыкның
квадрат булмавын исбатларга.
нокталарында булган дүрткырлыкның
квадрат булмавын исбатларга.
14.4.
![]() һәм
һәм
![]() векторларында төзелгән параллелограмм
диагональләре арасындагы
почмакны табарга.
векторларында төзелгән параллелограмм
диагональләре арасындагы
почмакны табарга.
14.5.
![]() ,
,
![]() ,
,
![]() ,
,
![]() нокталары
бирелгән.
нокталары
бирелгән.
![]() һәм
һәм
![]() векторлары
арасындагы почмакны табарга.
векторлары
арасындагы почмакны табарга.
14.6.
![]() һәм
һәм
![]() үзара
перпендикуляр ортлар.
үзара
перпендикуляр ортлар.
![]() векторының озынлыгын табарга.
векторының озынлыгын табарга.
14.7.
һәм
векторлары
![]() почмагы тәшкил итәләр һәм
почмагы тәшкил итәләр һәм
![]()
![]() Табарга
Табарга
![]()
14.8.
![]()
![]() векторлары
бирелгән. Табарга
векторлары
бирелгән. Табарга
![]() .
.
14.9. Дүрткырлыкның
![]()
![]()
![]()
![]() түбәләре бирелгән.
түбәләре бирелгән.
![]() һәм
һәм![]() диагональләренең үзара перпендикуляр
булуларын исбатларга.
диагональләренең үзара перпендикуляр
булуларын исбатларга.
14.10
![]()
![]()
![]() векторлары
бирелгән. Исәпләргә
векторлары
бирелгән. Исәпләргә
![]() .
.
14.11. Өчпочмакның
![]()
![]()
![]() түбәләре бирелгән. В
түбәсе янындагы эчке
почмакны табарга. 14.12. Түбәләре
түбәләре бирелгән. В
түбәсе янындагы эчке
почмакны табарга. 14.12. Түбәләре
![]()
![]()
![]() булган өчпочмакның эчке почмакларын
табарга һәм бу өчпочмакның тигезъянлы
булганлыгын исбатларга.
булган өчпочмакның эчке почмакларын
табарга һәм бу өчпочмакның тигезъянлы
булганлыгын исбатларга.
14.13.
һәм
векторлары
![]()
![]() почмагы
тәшкил итәләр һәм
почмагы
тәшкил итәләр һәм
![]() ,
,
![]() .
.
![]() һәм
һәм
![]() векторлары
арасындагы почмакны табарга.
векторлары
арасындагы почмакны табарга.
14.14.
![]()
![]() нокталары
бирелгән.
нокталары
бирелгән.
![]() векторы
юнәлешендәге күчәргә
векторы
юнәлешендәге күчәргә
![]() векторының проекциясен
табарга.
векторының проекциясен
табарга.
14.15.
һәм
векторлары
![]() почмагы
тәшкил итәләр һәм
почмагы
тәшкил итәләр һәм
![]() .
Табарга
.
Табарга
![]()
14.16.
![]()
![]()
![]() векторы бирелгән. Табарга
векторы бирелгән. Табарга
![]() .
.
14.17.
һәм
векторлары
почмагы
тәшкил итәләр һәм
![]() .
Табарга
.
Табарга
![]()
14.18.
векторы
![]() һәм
һәм![]() векторларына перпендикуляр
һәм
векторларына перпендикуляр
һәм
![]() шартын канәгатьләндерә.
векторын
табарга.
шартын канәгатьләндерә.
векторын
табарга.
14.19.
һәм
векторлары
![]() почмагы
тәшкил итәләр һәм
почмагы
тәшкил итәләр һәм
![]() .
Табарга
.
Табарга
![]()
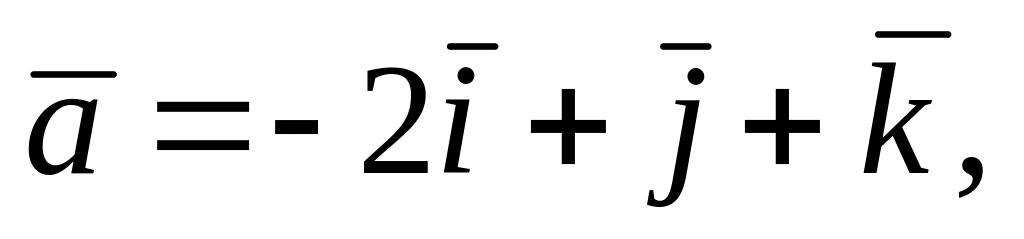
 ,
,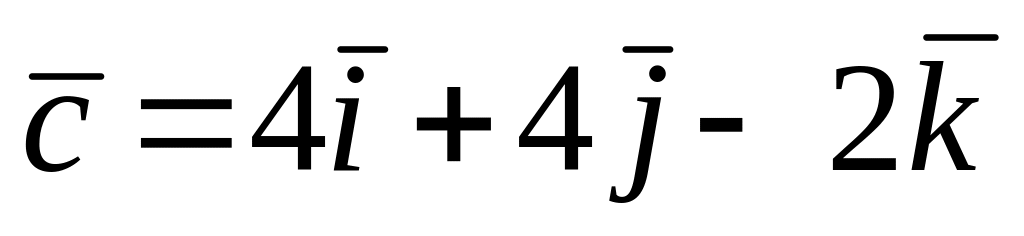 векторлары бирелгән. Табарга
векторлары бирелгән. Табарга
 .
.
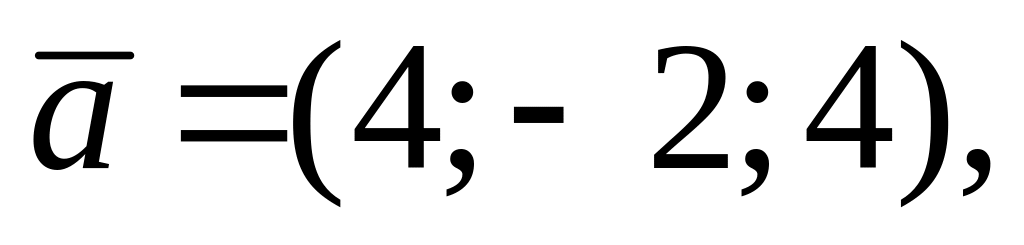
 векторлары бирелгән. Табарга
векторлары бирелгән. Табарга
векторы
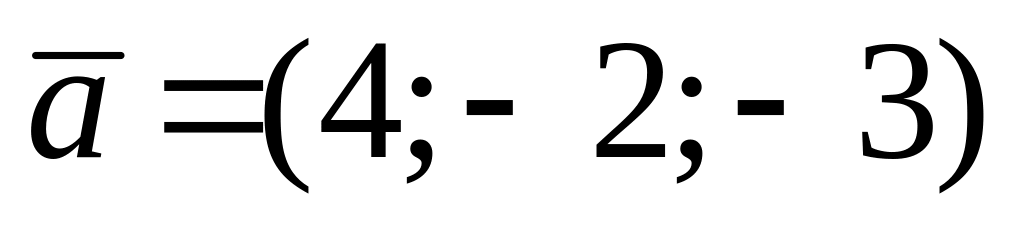 һәм
һәм
 векторларына перпендикуляр,
векторларына перпендикуляр,
 һәм ул Оу күчәре белән җәенке почмак
ясый. Аның координаталарын
табарга.
һәм ул Оу күчәре белән җәенке почмак
ясый. Аның координаталарын
табарга. векторы
юнщлеше белән тәңгәл килүче
күчәргә
векторы
юнщлеше белән тәңгәл килүче
күчәргә
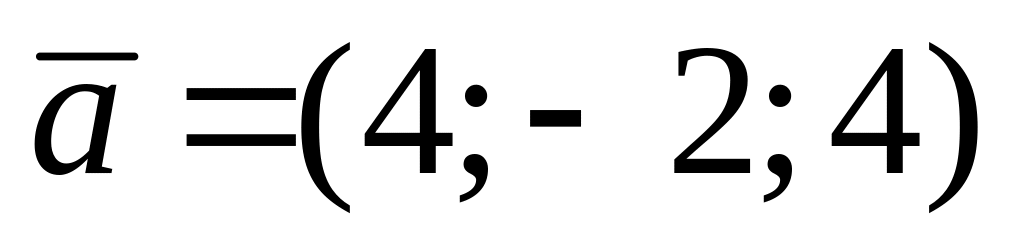 веторының
проекциясен табарга.
веторының
проекциясен табарга.

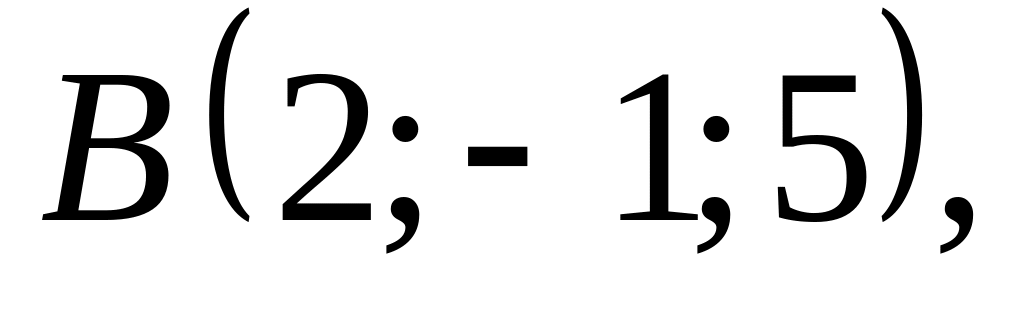
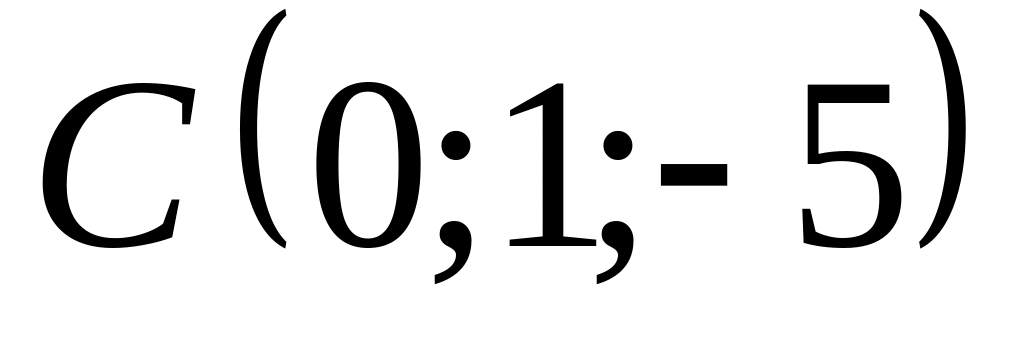 нокталары
бирелгән. Табарга
нокталары
бирелгән. Табарга
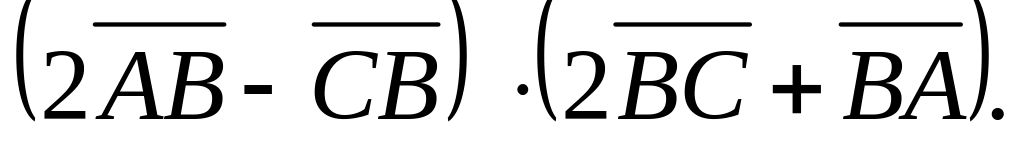
Oz күчәренә һәм
 векторына
перпендикуляр булган
векторына
перпендикуляр булган
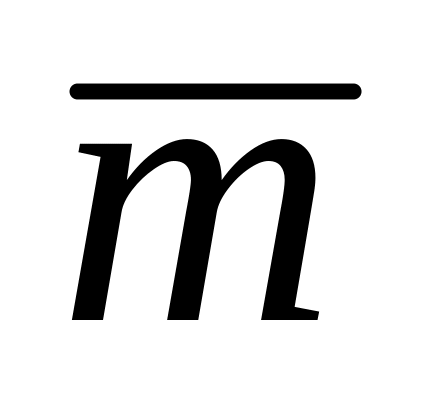 векторы
Оx күчәре белән кысынкы
почмак ясый һәм
векторы
Оx күчәре белән кысынкы
почмак ясый һәм
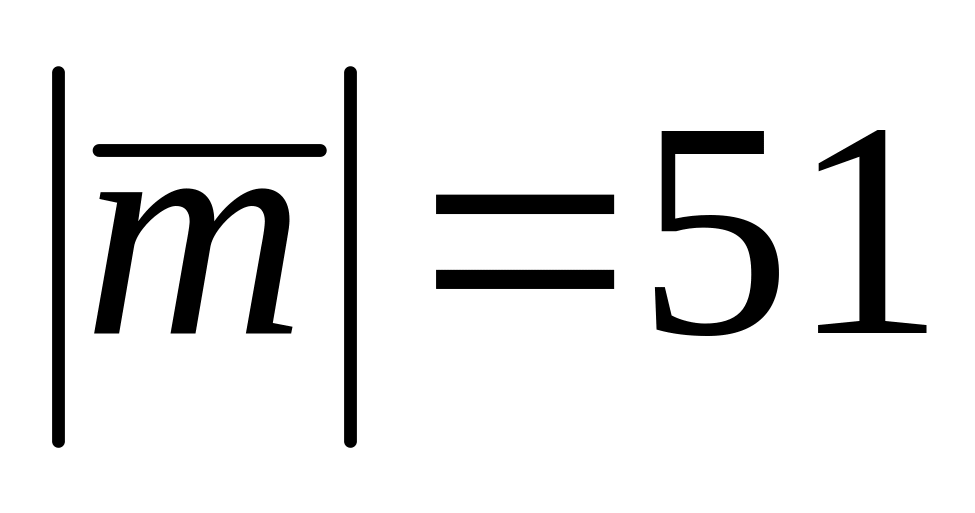 .
Аның координаталарын
табарга.
.
Аның координаталарын
табарга.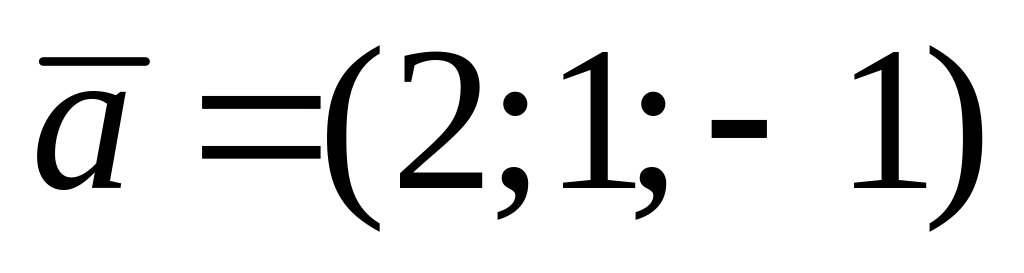 векторына
коллинеар һәм
векторына
коллинеар һәм
 шартын
канәгатьләндерүче
шартын
канәгатьләндерүче
 векторын табарга.
векторын табарга. һәм
һәм
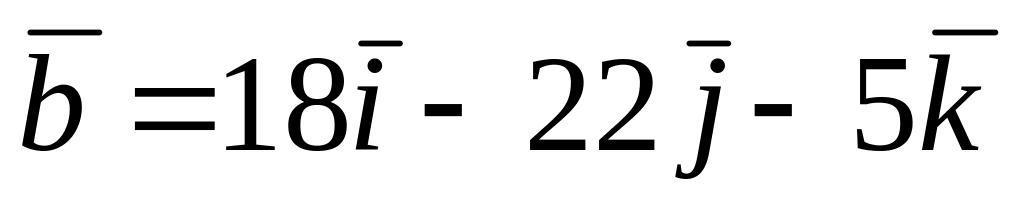 векторларына
перпендикуляр
векторы
Оy күчәре
белән җәенке почмак ясый һәм
векторларына
перпендикуляр
векторы
Оy күчәре
белән җәенке почмак ясый һәм
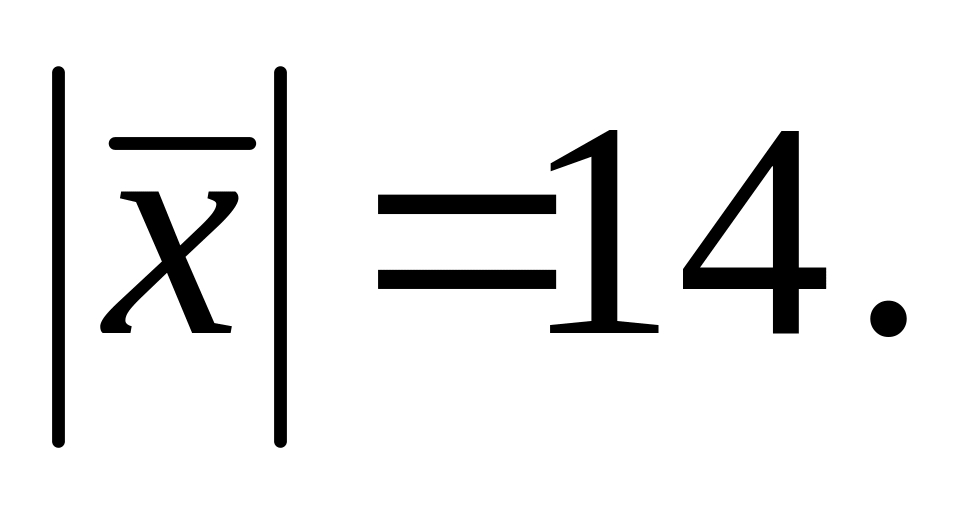 Аның координаталарын
табарга.
Аның координаталарын
табарга.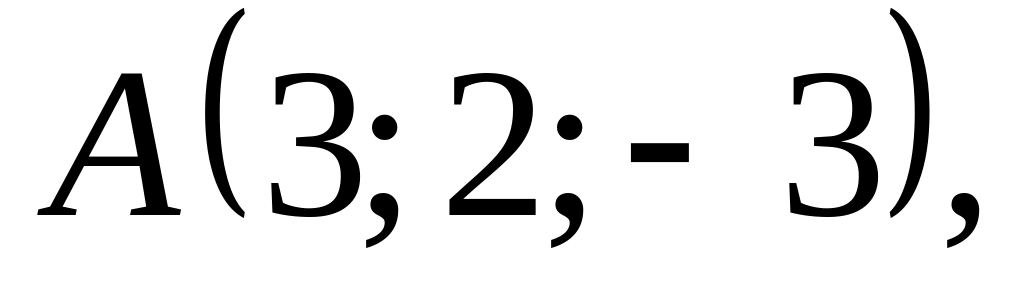

 өчпочмакның түбәләре
бирелгән. А түбәсе янындагы эчке
почмакны табарга.
өчпочмакның түбәләре
бирелгән. А түбәсе янындагы эчке
почмакны табарга.
Өч вектор бирелгән
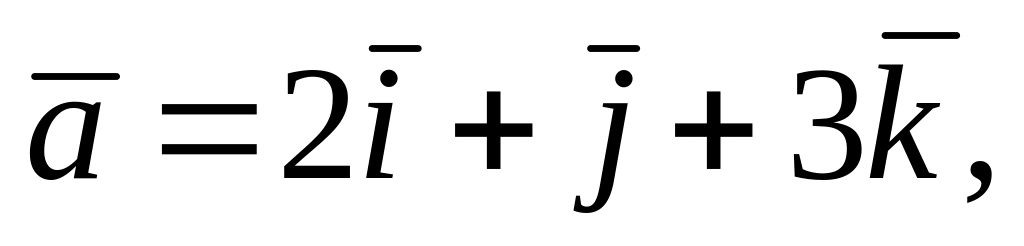
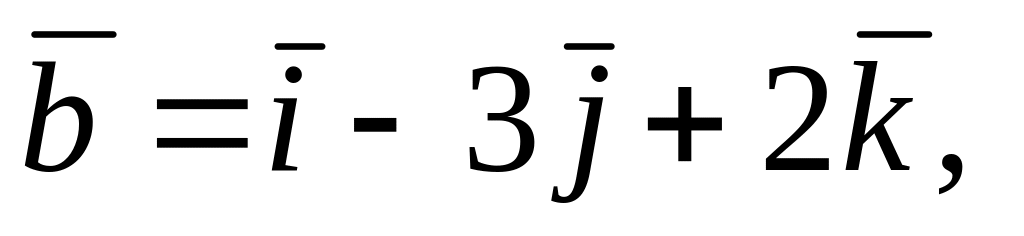

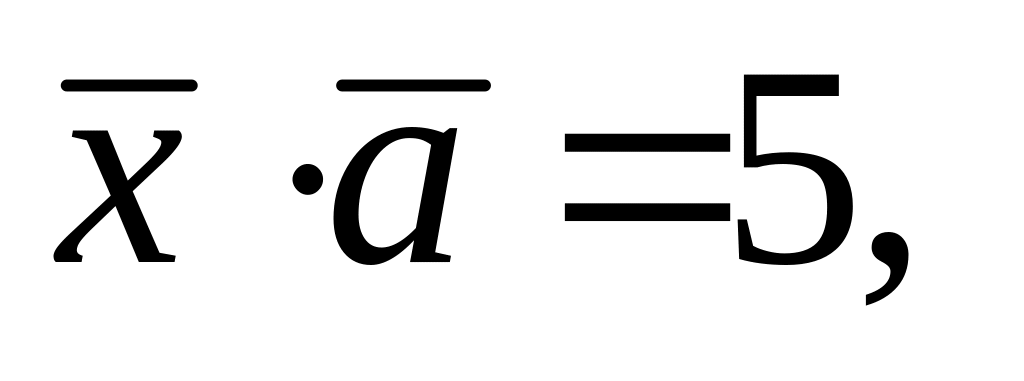
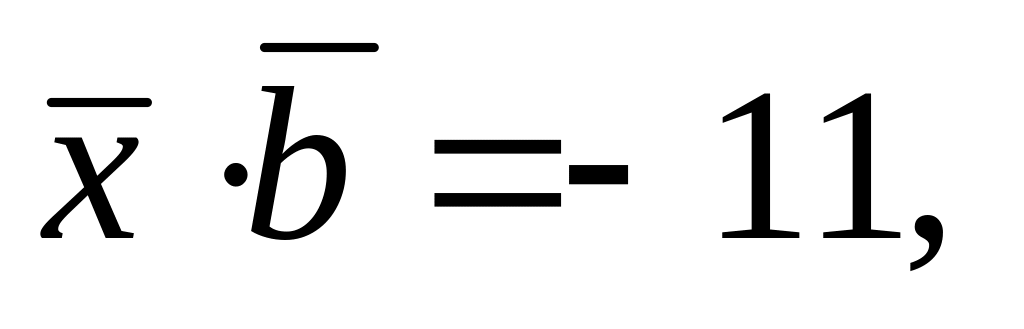
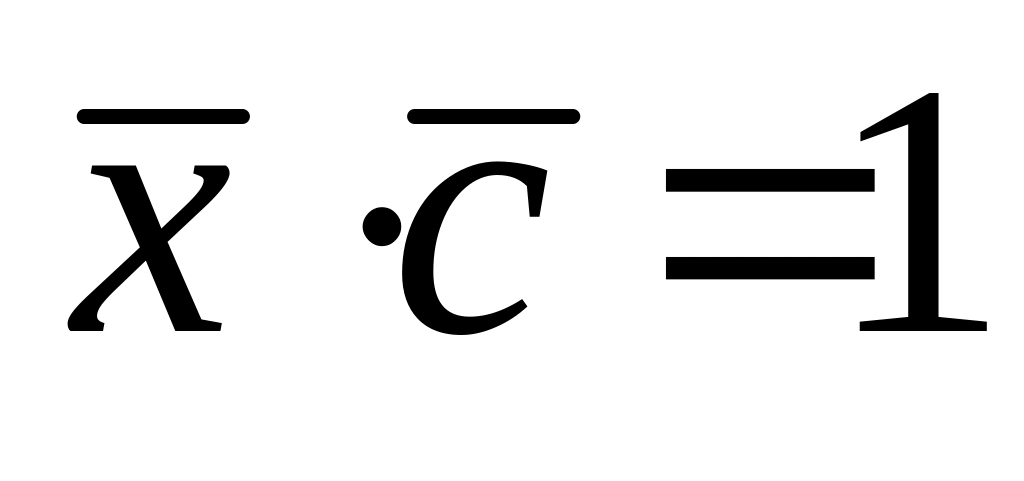 шартларын канәгатьләндерүче
векторын табарга.
шартларын канәгатьләндерүче
векторын табарга.Түбәләре

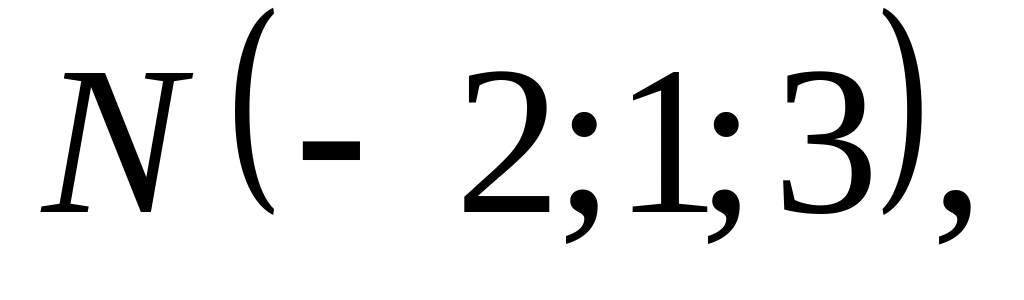
 нокталарында булган
өчпочмакның эчке почмаклары кысынкы
икәнлеген исбатларга.
нокталарында булган
өчпочмакның эчке почмаклары кысынкы
икәнлеген исбатларга.
