Векторларның вектор тапкырчыгышы.

һәм векторларының вектор тапкырчыгышы дип өченче вектор атала: . Ул түбәндәге шартларны канзгатьләндерә: 1) ;

2) һәм ;

3) - уң ориеттацияле векторлар.

Әгәр векторының очыннан караганда векторыннан векторына иң кыска борылыш сәгать теле йөрешенә каршы якка булса, компланар булмаган векторлар җыелмасы уң дип, ә каршы очракта сул дип атала.

Векторларның вектор тапкырчыгышы билгеләмәсеннән күренчәнчә:

.

Вектор тапкырчыгышының үзлекләре:

1) ; 2)

3) ; 4) , биредә - сан;

каноник базис векторлары өчен:

, , , , , .

Координаталары белән бирелгән һәм векторлары өчен вектор тапкырчыгышы түбәндәге формула ярдәмендә исәпләнә:

.

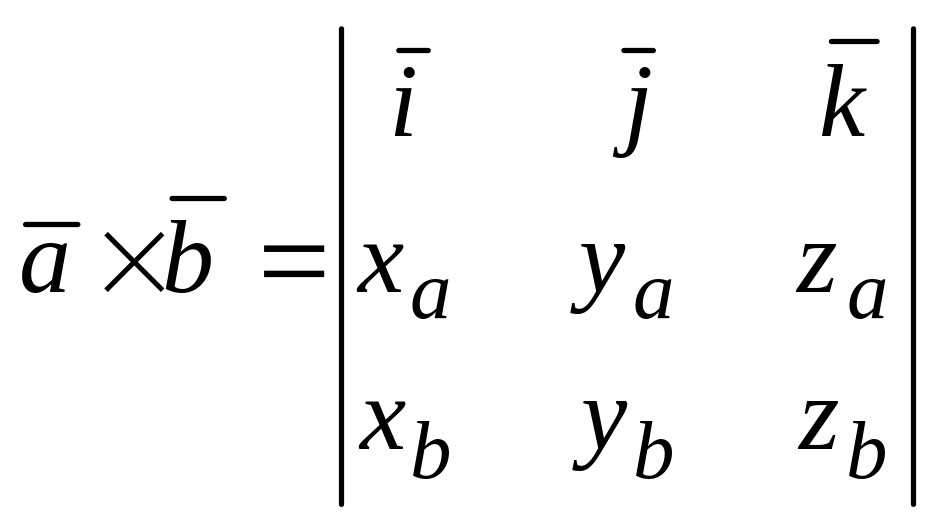Вектор тапкырчыгышның кайбер өстәмәләре:

1) Яклары һәм векторларында яткан өчпочмак һәм параллелограмм мәйданнары түбәндәге формула ярдәмендә исәпләнә:

.

2) һәм векторларының параллельлеген тикшерү: .

3) Фәзаның ниндидер О ноктасына карата ноктасына куелган кәченең моменты түбәндәге формула ярдәмендә исәпләнә: .

Мисал 1. һәм векторларында төзелгән параллелограмм мәйданын табарга, биредә , .

Чишү.

Параллелограмм мәйданы түбәндәге формула ярдәмендә исәпләнә:

.

Вектор тапкырчыгыш үзлекләрен кулланып, һәм векторларының вектор тапкырчыгышын табабыз:

,

чөнки , , .

Бу очракта

.

Җавап: .

Мисал 2. Түбәләре , , булган өчпочмак бирелгән. Аның мәйданын һәм биеклеген табарга.

Чишү.

өчпочмагының мәйданы векторларында төзелгән параллелограмм мәйданының яртысына тигез. һәм векторларының координаталарын табабыз:

, .

Бу векторларның вектор тапкырчыгышы түбәндәгечә табыла:

.

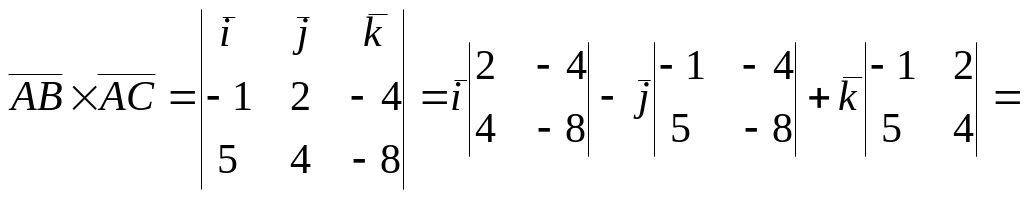
Димәк,

( мәйдан берәмлеге)

Икенче яктан

.

Моннан .

Димәк,

.

Җавап: .

2.71 Әгәр булса, исәпләргә:

а) ; б) .

2.72 Аңлатмаларны гадиләштерергә:

а) б) ;

в) ; г) .

2.73 векторларында төзелгән параллелограмм мәйданын табарга, биредә араларындагы почмак 60°булган берәмлек векторлар.

2.74 Диагональләре һәм векторлары булган параллелограмм мәйданын табарага, - берәмлек векторлар һәм

2.75 векторының координаталарын табарга:

a) б)

2.76 векторлары бирелгән. Векторның координаталарын табарга:

а) ; б) .

2.77 һәм нинди кыйммәтләр алганда векторы векторына коллинеар була:

а) ; б) .

2.78 Әгәр булса, векторын табарга.

2.79 Түбәләре , , нокталарында булган өчпочмакның мәйданын табарга.

2.80 Түбәләре нокталарында булган өчпочмакның биеклеген табарга.

2.81 векторлары бирелгән. , векторларына перпендикуляр һәм уңай ориентацияле булырлык итеп юнәлгән, берәмлек векторын табарга.

2.82 векторы Oz күчәренә һәм векторына перпендикуляр, Ox күчәре белән кысынкы почмак төзи. булганда аның координаталарын табарага.

2.83 һәм векторларына перпендикуляр, орты белән җәенке почмак төхүче һәм булган векторының координаталарын табарага.

2.84. һәм векторларына перпендикуляр, шартын канәгатьләндерүче векторының координаталарын табарага.

2.85 көче ноктасына куелган. Координата башлангычына карата бу көчнең моментын табарага.

2.86 көче ноктасына куелган. ноктасына карата бу көчнең моментын табарага.

2.87 ноктасына куелган өч көч бирелгән: . ноктасына карата бердәй тәэсир итүче көчнең озынлыгын һәм юнәлтүче косинусларын табарга.