41. Гипергеометриялық үлестірім және оның сандық сипаттамалары.
Дискретті ξ кездейсоқ шамасының гипергеометриялық үлестірімі болады , егер оның k=1,2,3,....,min(n;M) мәнінде
ықтималдықтары бар болса, мұндағы k=1,2,3,....,min(n;M), k≤N;n≤N;n,M,N – натурал сандар.
Алдыңғы
формуладан (
)
мынандай қатынас шығатынын атай кетелік:
Гипергеометриялық үлестірімнің математикалық күтімін табайық:
Қосынды
ішіндегі
–ды
түрінде жазып, сәйкес қысқартуларды
орындасақ, мынаны аламыз:
Біз
жоғарыда ортаңғы қосындыны (2)-формула
арқылы
түрінде жаздық. Енді
есептелік:
Бұдан
Теорема.
n,M,N параметрімен үлестірілген ξ кездейсоқ
шамасының гипергеометриялық үлестірімінің
математикалық күтімі:
Ал
дисперсиясы :
тең.
42. Бірқалыпты үлестірім. Анықтамасы және сандық сипаттамалары.
Ықтималдықтар тығыздығы
теңдiгiмен
анықталатын Х кездейсоқ шамасын
бiрқалыпты
үлестiрiмдi
(равномерное распределение) деп атайды.
Енді
f(x) бойынша интегралдық функция Ғ(х)
мәнін анықтайық. Ол үшін
формуласын пайдаланамыз.
Егер
х
a
болса, онда f(x)
= 0
болды.Сондықтан Ғ(х)
= 0.
Егер а<x
b
болғанда
.
болғанда
.
Демек,
Енді математикалық үмітті және дисперцияны табайық:
.
Демек,
.
43. Көрсеткішті үлестірім. Анықтамасы және сандық сипаттамалары.
Ықтималдық тығыздығы
мұндағы
параметр, теңдiгiмен анықталатын Х
кездейсоқ шамасын көрсеткiштiк
заң бойынша үлестiрiмдi
деп атайды.
Анықтама.
Егер Х кездейсоқ шамасы мына үлестірім
тығыздығы
арқылы
берілсе, онда ол көрсеткіштік үлестірім
заңымен берілген дейді. Мұндағы
- тұрақты оң шама.
Интегралдық функциясын табайық:
.
Сонымен
Бұл үлестірімнің сандық сипаттамалары:
=
яғни
.
яғни
Кездейсоқ шаманың (а; b) аралығынан мән қабылдау ықтималдығы
;
44. Гамма үлестірім. Анықтамасы және сандық сипаттамалары.
Гамма үлестірім. Математикалық талдау курсында меншіксіз және параметрлі интегралдар тобына жататын гамма функциясының анықтамасын еске түсірелік:
Сөйтіп,
параметрінің
функциясы
аралығында анықталған,
үздіксіз.Бұл функцияны есептеу
формуласына
негізделген.
(2)-формуласын дәлелдеу үшін бөліктеп интегралдаса болғаны:
Егер
n натурал сан болса,
Гамма үлестірімді ξ кездейсоқ шамасының тығыздық функциясы
(3)
Теңдіктерімен
анықталады, мұндағы α>0 және λ>0,
өйткені f(x)≥0 және
Гамма үлестірімнің сипаттауыш функциясы
Формуласымен,ал k-шы ретті моменті
формуласымен
есептеледі.
Олай болса, математикалық күтімі мен дисперсиясы табылды:
және
Гамма
үлестірімі арқылы бірқатар үлестірім
заңдарын шығарып алуға болады.Мәселен,
болса,гамма үлестірімі,көрсеткіштік
үлестірімге айналады.
45. Нормаль үлестірім. Анықтамасы және сандық сипаттамалары.
Үздіксіз кездейсоқ Х шамасының ықтималдықтар үлестірімін қалыпты деп атайды, егер оның ықтималдықтар үлестірім заңы ықтималдық тығыздығымен анықталса
.
(1)
мұндағы
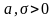нақты параметрлер
Бұл кездейсоқ шаманың математикалық
үмітін табайық:
,
яғни
.Сонымен
параметр
қалыпты заң үшін математикалық үміт
болады.Енді дисперсиясын табайық:
Өйткені мүшелеп интегралдасақ
болады.
Сонымен,
, ал
орташа квадраттық ауытқуы болады.Қалыпты
үлестірімі бар кездейсоқ шаманың
математикалық үміті мен дисперсиясын
есептеп отырып, оның анықтамасына
қатынасатын параметрлердің ықтималдық
мәнін аштық: бұл анықтамадағы
параметрі
математикалық үмітті, ал
параметрі дисперсияны көрсетеді.
Теорема.
Қалыпты үлестірімді кездейсоқ шаманың
берілген
аралығына түсу ықтималдығы
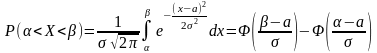.формуласы
бойынша анықталады, мұндағы
Лаплас функциясы.