34. Дискретті кездейсоқ шаманың дисперсиясы, орта квадраттық ауытқуы. Қасиеттері
Кездейсоқ шаманың мәндері оның математикалық үмітінен ауытқитындығы түсінікті. Міне, осы ауытқуды бағалау үшін дисперсия ұғымы енгізіледі. Х кездейсоқ шаманың дисперсиясын таңбасымен D(Х) белгіленеді:
Х-дискретті кездейсоқ шама, М(Х)-осы кездейсоқ шаманың математикалық үміті болсын. Бұл жағдайда Х-М(Х) айырмасын, кездейсоқ шама мәндерінің математикалық үміттен ауытқуы деп аталады. Кездейсоқ Х шамасының таралу заңы:
Х |
|
|
... |
|
|
Р |
|
|
... |
|
|
берілсін. Бұл жағдайда Х-М(Х) ауытқудың үлестірім заңы
Х-М(Х) |
|
|
... |
|
|
Р |
|
|
... |
|
|
Теорема.
Ауытқудың математикалық үміті нөлге
тең, яғни М
.
Дәлелдеу.
.
АНЫҚТАМА. Дискреттік Х кездейсоқ шамасының дисперсиясы деп кездейсоқ шаманың оның математикалық үмітінен ауытқуы квадратының математикалық үмітін айтады және оны былай белгілейді:
.
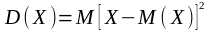Сонымен
дисперсияны анықтайтын
(2)
формуласы келіп шығады. Дисперсияның қасиеттері:
1-қасиет. Тұрақты шаманың дисперсиясы нөлге тең: D(С)=0, С=const.
Дәлелдеу.
(2)
формула бойынша
D(С)=М(С
2-қасиет.
Тұрақты
көбейткіш дисперсия белгісінің алдына
квадратталып шығады: D(СХ)=С
Дәлелдеу. Бұл қасиетті дәлелдеу үшін де (1) формуланы пайдаланамыз:
D(СХ)=М((СХ)
3-қасиет.Тәуелсіз екі кездейсоқ шамалардың қосындысының дисперсиясы олардың дисперсияларының қосындысына тең: (Х+У)=D(Х)+D(У).
Дәлелдеу.
(1)
формулаға математикалық үміттің
қасиеттерін қолданып, кездейсоқ
шамалардың тәуелсіздігін ескерсек,
Кездейсоқ шаманың алатын мәндерінің
оның орта мәнінен ауытқуын (шашырауын)
бағалау үшін тағы бір сандық сипаттама
орташа
квадраттық ауытқу
қолданылады
Орташа
квадраттық ауытқу деп дисперсиядан
алынған квадрат түбірді айтады, яғни
(3)
1-теорема. Егер тәжірибені бір рет жүргізгендегі А оқиғасының ықтималдығы р-ға тең болса q=1-p, ол оқиғаның пайда болу санының дисперсиясы pq-ға тең болады.
х |
1 |
0 |
|
P |
q |
Дисперсияны есептеп табайық:
М(Х)=
;
М(Х
,
D(Х)=М(Х
.
2-теорема.Егер бір тәжірибеде оқиғаның ықтималдығы р-ға тең болса q=1-p, ол оқиғаның тәжірибені n рет қайталағанда пайда болу санының дисперсиясы npq-ға тең болады, яғни D(Х)=npq.
Дәлелдеу.1-теорема бойынша бір тәжірибеде оқиғаның пайда болу санының дисперсиясы pq-ға тең. Тәжірибе n рет қайталанғандықтан, 3- қасиет бойынша pq+pq+…+pq=npq.
Мысал.Әрбіреуінде оқиғаның пайда болу ықтималы 0,3 болатын 15 тәуелсіз тәжірибе жүргізілген. Осы тәжірибедегі оқиғаның пайда болу саны –Х шамасының дисперсиясын табу керек.Шешуі. Есептің шарты бойынша n=15, p=0,3 олай болса q=1-0,3=0,7.
Сондықтан,
іздеп отырған дисперсиямыз: D(Х)=