Бернулли схемасы. Бернулли формуласы. 18.

Бернулли схемасындағы ең ықтимал табыс саны. 19.

Биномиаль үлестірім. Анықтамасы және сандық сипаттамалары. 37.

Бірқалыпты үлестірім. Анықтамасы және сандық сипаттамалары42..

Гамма үлестірім. Анықтамасы және сандық сипаттамалары. 44.

Гаустік кездейсоқ вектор және оның қасиеттері. 48.

Геометриялық үлестірім және оның сандық сипаттамалары. 39.

Гипергеометриялық үлестірім және оның сандық сипаттамалары. 41.

Екі өлшемді кездейсоқ шамалар. Олардың үлестірімі. 25.

Екі өлшемді нормаль (гаустік) үлестірім. 29.

Кездейсоқ шама: анықтамасы, үлестірім заңы, үлестірім функ және оның қасиеттері. 22.

Ковариация. Ковариациялық матрица. Қасиеттері. 46.

Комбинаторика эл-і. Комбинация. Қайталанымды комб(Алыну реті еск қайт таңд. Бльцман-Максвелл статист). 5.

Комбинаторика эл-і. Комбинация. Қайталанымсыз комб(Алыну реті еск қайт таңд. Орнал, Орын алмастыру). 6.

Комбинаторика эл-і. Комбинация. Өспелі комб(Бірмезгілде жасалатын таңд. Ферми-Дирак статистикасы). 7.

Корреляция коэффициенті. Қасиеттері. Корреляциялық матрица. 47.

Көп өлшемді кездейсоқ шамалардың (векторлардың) маргинал үлестірімдері. 26.

Көрсеткішті үлестірім. Анықтамасы және сандық сипаттамалары. 43.

Математкиалық статистикадағы бас жиынтық және таңдама. Вариациялық қатар. Полигон. Гистограмма53..

Муавр-Лапластың жергіліктік және интегралдық теоремалары. Қолданылу мысалдары. 21.

Нормаль үлестірілген өзара тәуелсіз кездейсоқ шамалардың қосындысының үлес қорыту. 32.

Нормаль үлестірім. Анықтамасы және сандық сипаттамалары. 45.

Орталық шектік теорема. Қолданылу мысалдары. 52.

Өзара тәуелсіз кездейсоқ шамалар. Тәуелсіз болу критерийлері 28.

Параметрлерді бағалау есебі. Нүктелік баға. Ығыспаған баға, тиянақты баға және тиімді баға. Мысалдары. 55.

Пуассон үлестірім. Анықтамасы және сандық сипаттамалары. 38.

Пуассонның жуықтау формуласы. 20.

Сенімділік инт-ы. Дисперсиясы белг нормаль үлестірімнен алынған таңд б-ша б-сіз матем күтімге сен-к инт. 56.

Сенімділік инт-ы.Матем күтімі белгілі норм үл-нен алынған таңд б-ша б-сіз дис сен-к инт. Хи-квадрат үл к ш.57.

Теріс биномиальді үлестірім. Анықтамасы және сандық сипаттамалары. 40.

Тәуелсіз сынақтар тізбегі 17.

Шартты үлестірім. Қасиеттері 27.

Ықтималдықтарды қосу формуласы. 12.

Эмпирикалық үлестірім функциясы. Белгісіз теориялық үлестірімге ықтималдық б-ша жинақталатындығы. 54.

1. Элментар оқиға. Элментар оқиғалар кеңістігі. Мысалдары.

2. Оқиғалар және оқиғаларға амалдар қолдану. Мысалдары.

3. Оқиға жиілігі, оның қасиеттері. Статистикалық орнықтылық.

4. Ықтималдық аксиомалары және олардың салдарлары

8. Ықтималдықтың классикалық анықтамасы.

9. Геометориялық ықтималдықтар. Кездесу туралы есеп.

10.Шартты ықтималдық және оның қасиеттері.

11. Ықтималдықтарды көбейту формуласы.

13. Оқиғалардың толық тобы. Толық ықтималдықтар формуласы.

14. Байес формуласы. Дәлелдеу және қолданылу мысалдары.

15. Тәуелсіз оқиғалар анықтамасы. Тәуелді және тәуелсіз оқиғаларға мысалдар.

16. Қос-қостан тәуелсіздік және жиынтық тәуелсіздік. Бернштейн мысалы.

23. Дискрет кездейсоқ шамалар: үлестірім қатары, үлестірім функциясы

24. Үзіліссіз кездейсоқ шамалар: үлестірім тығыздығы, үлестірім функциясы. Қасиеттері.

30. векторының үлестірімі арқылы түріндегі кездейсоқ шама үлестірімін табу мысалд.

31. Екі тәуелсіз кездейсоқ шаманың қосындысының үлестірімі. Үйірткі (свертка) форм.

33. Дискретті кездейсоқ шаманың математикалық күтімі. Қасиеттері.

34. Дискретті кездейсоқ шаманың дисперсиясы, орта квадраттық ауытқуы. Қасиеттері.

35. Үзіліссіз кездейсоқ шаманың математикалық күтімі. Қасиеттері.

36. Үзіліссіз кездейсоқ шаманың дисперсиясы, орта квадраттық ауытқуы. Қасиеттері

49. Чебышев теңсіздігі. Дәлелдеу.

50. Марков теңсіздігі. Дәлелдеу.

51. Үлкен сандар заңы.

1.Элементар оқиға. Элементар оқиғалар кеңістігі .мысалдары

2. Оқиғалар және оқиғаларға амалдар қолдану. Мысалдары.

3.Оқиға жиілігі, оның қасиеттері. Статистикалық орнықтылық.

8. Ықтималдық классикалық анықтамасы

Классикалық анықтамасы

Жалгасы келеси бетте

5.Комбинаторика элементтері. Комбинация. Қайталанымды комбициялар (Алыну реті ескерілетін қайтымды таңдамалар. Бльцман-Максвелл статистикасы).

6. Комбинаторика элементтері. Комбинация. Қайталанымсыз комбинациялар (Алыну реті ескерілетін қайтымсыз таңдамалар. Орналастырулар. Орын алмастырулар).

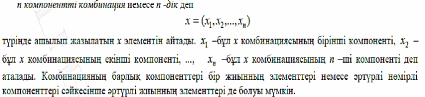
7.Комбинаторика элементтері. Комбинация. Өспелі комбинациялар(Бірмезгілде жасалатын таңдамалар. Ферми-Дирак статистикасы).

9. Геометориялық ықтималдықтар. Кездесу туралы есеп.

`

10. Шартты ықтималдық және оның қасиеттері.

Дәлелдеуі. Белгілеулер енгіземіз: n- саны А олқиғасының пайда болуын немесе болмауын білдіретін жалпы нәтижесінің саны;

- саны А оқиғасының пайда болуына қолайлы нәтижелер саны;

m- саны В оқиғасының пайда болуын немесе болмауын білдіретін жалпы нәтижесінің саны; - саны В оқиғасының болуына қолайлы жағдайлар саны; nm- саны АВ оқиғасының болуының жалпы саны; - саны АВ оқиғасының пайда болуна қолайлы жағдайлар саны. Сонымен анықтама бойынша: Р(АВ)= Р(А)Р(В).

11. Ықтималдықтарды көбейту формуласы.

Дәлелдеуі. Белгілеулер енгіземіз:

n- саны А олқиғасының пайда болуын немесе болмауын білдіретін жалпы нәтижесінің саны;

- саны А оқиғасының пайда болуына қолайлы нәтижелер саны;

m- саны В оқиғасының пайда болуын немесе болмауын білдіретін жалпы нәтижесінің саны;

- саны В оқиғасының болуына қолайлы жағдайлар саны;

nm- саны АВ оқиғасының болуының жалпы саны;

- саны АВ оқиғасының пайда болуна қолайлы жағдайлар саны.

Сонымен анықтама бойынша:

Р(АВ)= Р(А)Р(В).

Мысал. Екі жәшікке дайындалған деталь салынған. Бірінші жәшікте 10 деталь, оның үшеуі стандартты, екіншісінде – 15 деталь, оның алтауы стандартты. Әрбір жәшіктен бір-бірден кез келген деталь алынды. Алынған екі детальдің де стандартты екенінің ықтималдығын табу керек.

Шешуі. Белгілеу енгізелік. А- бірінші жәшіктен алынған деталь стандартты, В- екінші жәшіктен алынған деталь стандартты. Сондықтан Р(А)=3/10, Р(В) =6/15. Алынған екі деталь де стандартты болуы үшін АВ оқиғасы пайда болуы керек. Бұл екі оқиға да үйлесімді, себебі екеуі бірдей пайда бола алады, сондай – ақ бұл оқиғалар тәуелсіз, себебі оқиғалардың пайда болуы бір-біріне байланныссыз. Сондықтан формуланы пайдалануға болады:

Р(АВ)= Р(А)Р(В)=0,12.

12.Ықтималдықтарды қосу формуласы

1.Үйлесімсіз оқиғалардың ықтималдығын қосу теоремасы. Егер А мен В оқиғалары үйлесімсіз оқиғалар болса, онда олардың қосындысының ықтималдығы олардың ықтималдықтарының қосындысына тең:

_.

Дәлелдеу. Барлық жағдайлар саны n, ал А мен В-ға қолайлы жағдайлар саны сәйкес мен болсын. Сонда , , 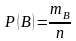А және В оқиғалары үйлесімсіз болғандықтан А+В қосындысына + жағдайлары қолайлы болады. Демек,

Салдар. Егер қос-қостан үйлесімсіз оқиғалар болса, онда бұл оқиғалардың қосындысының ықтималдығы әрбіреуінің ықтималдықтарының қосындысына тең болады, яғни

1-мысал. Жәшікте 15 ақ, 5 қара шар бар. Жәшіктен қалай болса солай 2 шар алынған. Сол алынған шарлардың бірдей түсті болу ықтималдығын табу керек.

Шешуі: Жәшіктегі 20 шардан 2 шар алынып отыр. Олай болса, барлық жағдайлар саны . Алынған екі шардың бірдей түсті болу оқиғасын А деп белгілейік. Енді «екі шар ақ түсті», «екі шар қара түсті» оқиғаларын В, С әріптерімен белгілейік. В-ға қолайлы жағдайлар саны 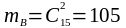; С-ға . Олай болса, . Ал, А=B+C қосу теоремасын қолдансақ,

14. Байес формуласы. Дәлелдеу және қолданылу мысалдары.

15. Тәуелсіз оқиғалар анықтамасы. Тәуелді және тәуелсіз оқиғаларға мысалдар.

16. Қос-қостан тәуелсіздік және жиынтық тәуелсіздік. Бернштейн мысалы.