Булевы функции от 1-ой и 2-х переменных
Представим вначале в табличном виде все булевы функции от 1-ой переменной. Как мы знаем, их всего четыре.
Таблица 3.2. Булевы функции от 1-ой переменной |
||||
x1 |
f1 |
f2 |
f3 |
f4 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
В этой таблице представлены следующие функции:
f1(x1)= 0 - константа 0;
f2(x1)= 1 - константа 1;
f3(x1)= x1 - тождественная функция;
f4(x1)= ¬ x1 - отрицание x1 (используется также обозначение x 1 , а в языках программирования эта функция часто обозначается как NOTx1 ).
В следующей таблице представлены все 16 функций от 2-х переменных.
Таблица 3.3. Булевы функции от 2-х переменных |
|||||||||||||||||
x1 |
x2 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
f16 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Многие из этих функций часто используются в качестве "элементарных" и имеют собственные обозначения.
f1(x1,x2)= 0 - константа 0;
f2(x1,x2)= 1 - константа 1;
f3(x1,x2)= x1 - функция, равная 1-му аргументу ;
f4(x1,x2)= ¬ x1 - отрицание x1 ;
f5(x1,x2)= x2 - функция, равная 2-му аргументу ;
f6(x1,x2)= ¬ x2 - отрицание x2 ;
f7(x1,x2)= (x1
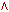x2)
- конъюнкция,
читается "
x1
и x2
" (используются
также обозначения (x1
& x2)
, (x1x2)
, min(x1,x2)
и (x1
AND x2)
);
f8(x1,x2)= (x1
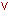x2)
- дизъюнкция,
читается "
x1
или x2
" (используются
также обозначения (x1
x2)
, (x1
+ x2)
, max(x1,x2)
и (x1
OR x2)
);
f9(x1,x2)= (x1 x2) - импликация, читается "x_1 влечет x_2" или "из x1 следует x2 " (используются также обозначения ( x1
x2
), и (
IF x1
THEN x2
));
f10(x1,x2)= (x1 + x2) - сложение по модулю 2, читается " x1 плюс x2 " (используется также обозначение (x1 x2) );
f11(x1,x2)= (x1 ~ x2) - эквивалентность, читается " x1 эквивалентно (равносильно) x2 " (используется также обозначение (x1 x2) );
f12(x1,x2)= (x1 | x2) - штрих Шеффера (антиконъюнкция), иногда читается как "не x1 и x2 ";
f13(x1,x2)= (x1
x2)
- стрелка
Пирса (антидизъюнкция),
иногда читается как "не x1
или x2
".
В качестве элементарных функций будем также рассматривать 0-местные функции-константы 0 и 1.
Отметим, что функции f1(x1,x2) и f2(x1,x2) фактически не зависят от значений обоих аргументов, функции f3(x1,x2) и f4(x1,x2) не зависят от значений аргумента x2, а функции f5(x1,x2) и f6(x1,x2) не зависят от значений аргумента x1.
Определение 3.1. Функция f(x1,…, xi,…, xn) не зависит от аргумента xi, если для любого набора значений σ1,…,σi-1>, σi+1,…, σn остальных аргументов f имеет место равенство
Такой аргумент xi называется фиктивным. Аргументы, не являющиеся фиктивными, называются существенными.
Функции f1(x1,…, xn) и f2(x1,…,xm) называются равными, если функцию f2 можно получить из функции f1 путем добавления и удаления фиктивных аргументов.
Например, равными являются одноместная функция f3(x1) и двухместная функция f3(x1,x2) , так как вторая получается из первой добавлением фиктивного аргумента x2 . Мы не будем различать равные функции и, как правило, будем использовать для обозначения равных функций одно и то же имя функции. В частности, это позволяет считать, что во всяком конечном множестве функций все функции зависят от одного и того же множества переменных.