Отношения и функции. Мощность множества

Бинарным или двуместным отношением между элементами множеств A и B называется любое подмножество R их декартова произведения A × B . Говорят также, что R является отношением из A в B. При A = B отношение R называется бинарным отношением на A. Вместо (x,y) R часто пишут xRy. Например, для отношений порядка на множестве натуральных чисел N используют записи вида 3 7, x 23, z > y и т.п.

Тождественным отношением на множестве A называется отношение

I_A= {(x,x)| x A}. Его обозначают знаком равенства "=".

С бинарным отношением R связана его область определения:

и его область значений:

Обратным отношением для бинарного отношения R называется множество пар R^-1 = {(x,y)| (y,x) R}.

Образом множества X относительно R называется множество R(X) = { y| существует x X такое, что (x,y) R}, прообразом X относительно R называется R^-1(X).

Произведением отношений R₁ A × B и R₂ B × C называется следующее отношение R₁ ˆ R₂ A × C :

Важную роль среди бинарных отношений играют отношения эквивалентности. Бинарное отношение R на множестве A называется отношением эквивалентности, если для него выполнены следующие условия:

1. Рефлексивность: для любого a A (a,a) R ;

2. Симметричность: для любых a, b из A (a,b) R (b,a) R;

3. Транзитивность: для любых трех элементов a, b,c из A, если (a,b) R и (b,c) R, то и (a,c) R.

Примером отношения эквивалентности на множестве натуральных чисел N является равенство остатков при делении на некоторое фиксированное число n: a = b (mod n).

С каждым отношением эквивалентности на множестве A связано разбиение A на непересекающиеся подмножества - классы эквивалентности. Для каждого a A его класс эквивалентности [a] включает все эквивалентные a элементы: . Из определения эквивалентности непосредственно следует, что, если , то , а если , то . Таким образом, разбиение A на классы эквивалентности не зависит от выбора конкретных представителей этих классов в качестве их имен.

Если в приведенном выше примере в качестве n взять, например, 5, то все числа из N разобьются на 5 классов эквивалентности: N₀, N₁, N₂, N₃, N₄, где в класс N_i (i=0,1,2,3,4) войдут числа, дающие при делении на 5 остаток i.

Еще один важный класс отношений - отношения (частичного) порядка. Бинарное отношение R на множестве A называется отношением частичного порядка, если для него выполнены следующие условия:

1. Антирефлексивность: для любого a A \ (a,a) R ;

2. Антисимметричность: для любых a, b из A, если (a,b) R и (b,a) R, то a = b;

3. Транзитивность: для любых трех элементов a, b,c из A, если (a,b) R и (b,c) R, то и (a,c) R.

Примером такого отношения является отношение строгого включения на множестве 2^A всех подмножеств некоторого множества A. Обычное отношение строгого порядка < на Nтакже удовлетворяет условиям 1 - 3. Но для него выполнено еще одно существенное условие:

4. Линейность: для любых a, b из A либо (a,b) R, либо (b,a) R.

Отношения, для которых выполнены условия 1 - 4 называются отношениями линейного порядка.

Отношение f называется функцией из A в B ( из A на B) , если _f=A, ρ_f B (соответственно, ρ_f = B) и для всех x, y₁, y₂ из того, что (x,y₁) f и (x,y₂) f, следует, что y₁ = y₂. Запись: f : A B. В качестве синонимов термина "функция" часто используются слова отображение и преобразование. Если f функция, то вместо (x,y) f пишем f(x) = y и называем y значением f на аргументе x. f называется 1-1-функцией (или обратимой функцией), если для любых x₁, x₂, y из того, что f(x₁) = y и f(x₂) = y следует, что x₁ = x₂. Функция f : A B называется взаимно однозначной функцией, если она является 1-1-функцией и ρ_f=B. Взаимно однозначная функция f : A A называется перестановкой множества A.

Определения бинарных отношений и функций с одним аргументом естественным образом обобщаются на многоместные отношения и функции.

n-арным (или n- местным) отношением на множествах A₁,…, A_n называется любое подмножество A₁ × … × A_n. Функцию f : A₁ × … × A_n B называем n-арной (или n- местной) функцией и пишем f(x₁, …, x_n) = y при x₁ A₁, … , x_n A_n. Чаще всего мы будем рассматривать n-арные функции для A₁ = … = A_n =A. В этом случае f : Aⁿ B будем называть n-арной функцией из A в B.

Множество A называется эквивалентным (по мощности) множеству B, если между A и B можно установить взаимно однозначное соответствие. Мощностью множества A называется класс всех множеств, эквивалентных множеству A, и эта мощность обозначается через |A|.

Для каждого n N мощность множества N_n={0,1,…,n-1} обозначим через n. Множество называется конечным, если оно для некоторого n N эквивалентно множеству N_n. Для конечных множеств их мощность - это количество элементов. В частности, для пустого множества | | = 0.

Каждое множество, эквивалентное N, называется счетным и его мощность обозначается .

В нашем курсе мы будем рассматривать только конечные и счетные множества, а также - отношения и функции на таких множествах. Отметим, что многие объекты, изучаемые в дискретной математике, являются частными случаями отношений и функций на конечных множествах. К ним относятся, в частности, слова. Пусть алфавит A={a₁, …, a_m} - это конечное множество элементов, называемых символами (буквами). Слово в алфавите A - это конечная последовательность символов этого алфавита: w =w₁ … w_n, w_i A при i = 1, …, n . Число букв в этой последовательности называется длиной слова и обозначается |w|. Имеется одно специальное "пустое" слово длины 0. Будем обозначать его через ε. Нетрудно понять, что слова длины n взаимно однозначно соответствуют функциям вида f: {1,…, n} A. А именно, слову w = w₁… w_n, соответствует функция f_w(i) = w_i, i = 1, …, n. Языком в алфавите A называется произвольное множество слов этого алфавита. На языках, как и на множествах, определены операции объединения, пересечения и разности. Язык, включающий все слова в алфавите A ( в том числе и пустое), обычно обозначается через A^*. Дополнение языка L A^* это язык L = A^* \ L

Задачи

Задача 1.1. Доказать следующие включения:

• A B A A B;

• A \ B A.

Задача 1.2. Доказать следующие тождества:

• A A = A A = A;

• A (B C) = (A B) (A B);

• (A B) A= (A B) A = A;

• A \ (B C) = (A \ B) ( A\ C);

• A \ (B \ C) = (A \ B) ( A C);

• A = A=A ;

• A = A= ;

• A = A=A;

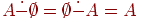• и .

Задача 1.3. Найти все подмножества множеств , { }, {1,2,3}, {a,{1,2}, }.

Задача 1.4. Пусть A={ 0, 1}, B ={a,b,c}. Определите множества A× B и B × A.

Задача 1.5. Доказать, что

• A × (B C) = (A× B) (A× C);

• A × (B C) = (A× B) (A× C);

• A × (B \ C) = (A× B)\ (A× C);

• если A B и C D, то (A × C) = (A× D) (B × C).

Задача 1.6. Для каждого из следующих отношений определить _R, ρ_R, R^-1, Rˆ R, Rˆ R^-1:

• R = {(x,y) | x,y N и x делит y };

• R = {(x,y) | x,y N и x + y 10 };

• R = {(x,y) | x,y N и y= 3x + 1 };

• R = {(x, x²) | x N textrm{ и } x 10};

• R = {(a,b), (b,c), (b,d), (c,d), (d, b)}.

Задача 1.7. Пусть множество S ={ (i, j) | 1 i, j 8} задает клетки шахматной доски. Опишите следующие бинарные отношения на S:

• L ={ (a,b) | ладья за 1 ход может перейти с клетки a на клетку b };

• K= { (a,b) | конь за 1 ход может перейти с клетки a на клетку b }.

Будут ли эти отношения эквивалентностями ? Опишите отношение L ˆ L.

Задача 1.8. Пусть Π - множество прямых на плоскости. Будут ли следующие отношения отношениями эквивалентности:

• параллельность прямых;

• перпендикулярность прямых.

Задача 1.9. Пусть A={a₁,…, a_m} - произвольный конечный алфавит. Обозначим через Aⁿ множество слов длины n в алфавите A (это обозначение согласовано с тем же обозначением декартовой степени A, так как степень Aⁿ состоит из всех последовательностей элементов A длины n). Через A^* обозначим множество всех слов в алфавите A.

• Определим следующее отношение R₁ на словах из Aⁿ.

Пусть v=a_{i₁}a_{i₂}… a_{i_n}, . Тогда

(v,w) R₁ для всех k от 1 до n i_k j_k и для некоторого такого k i_k < j_k, т.е. номер каждой буквы слова v не больше номера той же буквы в слове w и хотя бы у одной из букв он меньше.

Является ли это отношение R₁ отношением частичного (линейного) порядка?

• Определим следующее отношение R₂ на словах из A^*.

Пусть v=a_{i₁}a_{i₂}… a_{i_n}, . Тогда

(v,w) R₂ существует такое k в интервале от 1 до n, что при l < k i_l = j_l и i_k < j_k или n < r и первые n символов w совпадают со словом v.

Является ли это отношение R₂ отношением частичного (линейного) порядка?

Замечание. Определенное в пункте (а) отношение R₁ называется отношением покоординатного порядка, а отношение R₂ из пункта (б) - отношением лексикографического порядка. В соответствии с лексикографическим порядком упорядочены, например, слова в словарях и энциклопедиях.

Задача 1.10. Доказать, что если множества A и B конечны, то

• | A × B| = |A| · |B|;

• |A B| = |A|+ |B| - |A B|.