Алгоритм БыстроеЗамыкание(X,f)

I) Инициализация:

1. ДЛЯ КАЖДОГО процесса t F ВЫПОЛНЯТЬ

2. { СЧЕТ[t] := |L_t|;

3. ДЛЯ КАЖДОГО a L_t ВЫПОЛНЯТЬ

4. добавить t в СПИСОК[a];

5. } ;

6. НОВЫЕ := X; ОБНОВА := X;

II) Вычисление:

7. ПОКА ОБНОВА ВЫПОЛНЯТЬ

8. { выбрать a ОБНОВА; ОБНОВА := ОБНОВА \ {a};

9. ДЛЯ КАЖДОГО t СПИСОК[a] ВЫПОЛНЯТЬ

10. { СЧЕТ[t] := СЧЕТ[t] - 1;

11. ЕСЛИ СЧЕТ[t] = 0

12. ТО

13. ЕСЛИ {b_t} НОВЫЕ

14. ТО { НОВЫЕ := НОВЫЕ { b_t};

15. ОБНОВА := ОБНОВА {b_t} }

16. }

17. };

18. вернуть(НОВЫЕ).

Следующая теорема утверждает корректность приведенного алгоритма.

Теорема 6.3. Алгоритм БыстроеЗамыкание(X,F) строит замыкание .

Доказательство этого утверждения аналогично доказательству теоремы 6.2 (см. задачу 6.3).

Отметим, что число шагов алгоритма БыстроеЗамыкание(X,F) пропорционально размеру его входа, т.е. числу продуктов в F и X или числу букв в записи формулы (*). Такие алгоритмы называются работающими в линейное (от размера входа) время или, просто, линейными. Действительно, при инициализации каждый элемент F рассматривается 2 раза, а в основном цикле общее число рассматриваемых элементов и операций уменьшения на 1 значений СЧЕТ[t] в стр.10 алгоритма не больше суммы размеров всех L_t, т.е. также не превосходит размера входа.

Пример 6.3. Рассмотрим работу алгоритма БыстроеЗамыкание на следующем примере. Пусть A={a, b, c, d, e, f, g, h}, X = { b,f}, а множество F состоит из следующих 6 процессов:

1. a,b,c,h d;

2. b,c,d a;

3. g,b e;

4. e,f c;

5. f,e d;

6. b,f g.

Тогда при инициализации будут построен массив СЧЕТ = [4, 3, 2, 2, 2, 2] и следующие списки:

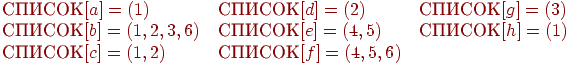
Множества ДОБАВКА и НОВЫЕ будут инициализированы в стр. 6 булевскими массивами 01000100 с 1 на местах, соответствующих продуктам b и f. Дальнейшие изменения этих структур представлены в следующей таблице.

СЧЕТ						ДОБАВКА	НОВЫЕ
1	2	3	4	5	6	abcdefgh	abcdefgh
4	3	2	2	2	2	01000100	01000100
3	2	1	2	2	1	00000100	01000100
3	2	1	1	1	0	00000010	01000110
3	2	0	1	1	0	00001000	01001110
3	2	0	0	0	0	00110000	01111110
2	1	0	0	0	0	00010000	01111110
2	0	0	0	0	0	10000000	11111110
1	0	0	0	0	0	00000000	11111110

Алгоритм завершает работу, когда множество ДОБАВКА становится пустым. В этот момент результат Cl(X,F) представлен множеством НОВЫЕ. В нашем примере оно равно {a,b,c, d,e,f,g}.

Задачи

Задача 6.1. Докажите, что последовательность процессов τ_i в доказательстве теоремы 6.1 определена корректно, т.е. все исходные продукты каждого процесса в этой последовательности имеются перед его запуском.

Задача 6.2. Докажите теорему 6.2.

Указание. Пусть X_k - это состояние множества НОВЫЕ после k итераций основного цикла алгоритма ЗАМЫКАНИЕ в строках 2-6. Покажите, что для каждого продукта z Cl(X,F), который может быть получен из X последовательностью процессов длины k, z входит в X_k.

Задача 6.3. Алгоритм ПрямаяВолна(X,y,F) позволяет ответить на вопрос о возможности производства y из исходных продуктов X с помощью процессов F, но в случае положительного ответа не строит последовательность процессов, приводящую к y. Измените алгоритм ЗАМЫКАНИЕ(X,F) так, чтобы по его результату для любого продукта a Cl(X,F) можно было построить последовательность процессов, приводящую к a.

Задача 6.4. Назовем сложным технологическим процессом (или производством)} такой процесс t, который по набору исходных продуктов L_t производит некоторое множество продуктов B_t (а не один продукт b_t). Обобщите алгоритм ЗАМЫКАНИЕ(X,F) так, чтобы он строил замыкание X относительно системы сложных технологических процессов F.

Задача 6.5. Определите, какая последовательность процессов в примере 6.3 приводит к получению a.

Задача 6.6. Используя алгоритм ЗАМЫКАНИЕ (X,F), вычислить замыкание для набора исходных продуктов X = { c,d} и следующей системы технологических процессов F:

1. a,b,d h;

2. a,c,d,g f;

3. d,g b;

4. e,f c;

5. b,k a;

6. d,c k;

7. h,d,c g;

8. d,g ,a e;

9. c, d, k h.

Определите, какая последовательность процессов приводит к получению e.

Задача 6.7. Докажите теорему 6.3.

Указание. Пусть X_k - это состояние множества НОВЫЕ после k итераций основного цикла алгоритма БыстроеЗамыкание в строках 7-17. Покажите, что

• если на (k+1)-ой итерации основного цикла для некоторого процесса t обнаруживается, что СЧЕТ[t] = 0, то L_t X_k;

• для каждого продукта z Cl(X,F), который может быть получен из X последовательностью процессов длины k, z входит в X_k;

• условие ОБНОВА = выхода из основного цикла выполнено после (k+1)-ой итерации тогда и только тогда, когда X_k= X_k+1.

Задача 6.8. Измените алгоритм БыстроеЗамыкание так, чтобы по его результату для любого продукта a Cl(X,F) можно было построить последовательность процессов, приводящую к a.

Задача 6.9. Используя алгоритм БыстроеЗамыкание, вычислить замыкание для набора исходных атрибутов X = { a,f} и следующей системы зависимостей F:

1. a,b,c h;

2. a,c,d,g h;

3. e,f c;

4. f,a d;

5. g,d e;

6. d,f ,a g.

Определите, какая последовательность процессов приводит к получению h