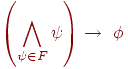6. Лекция: Хорновские формулы и задача получения продукции Содержание

• Хорновские формулы

• Задача получения продукции

• Решение задачи о продукции

  • Алгоритм ЗАМЫКАНИЕ(X,F)

  • Алгоритм ПрямаяВолна(X,y,F)

  • Алгоритм БыстроеЗамыкание(X,F)

• Задачи

Хорновские формулы

Определим вначале один интересный класс булевых формул - Хорновские формулы.

Определение 6.1. Пусть A - это множество логических (булевых) переменных. Хорновская (H-) формула - это формула вида

где a_i, b A

Содержательно, такая Хорновская формула утверждает, что из истинности всех условий набора {a₁, a₂, … , a_r} следует истинность заключения b. Утверждения такого вида находят широкое применение в различных разделах информатики. В частности, в теории баз данных такой вид имеют "функциональные зависимости", в логическом программировании - правила логических программ, в автоматическом синтезе программ - "аксиомы вычислимости". В таком же виде формулируются правила вывода во многих экспертных системах.

В этих и других областях представляют интерес связанные между собой задачи о минимальности набора H-формул и о выводимости некоторой H-формулы из заданного набора H-формул. Первая задача состоит в выяснении того, входит ли в набор H-формул F некоторая формула , которая может быть удалена из F без потери информации, т.е. которая выводится из F \ { }, а это и есть задача о выводимости. Уточним эту задачу.

Определение 6.2. H-формула является следствием или выводится из множества H-формул F, если на всяком наборе значений переменных из A, на котором истинны все формулы из F, истинна и (будем это обозначать как ).

Это понятие следования некоторой формулы из множества формул можно сформулировать и для произвольных булевых формул, а не только для Хорновских. Следующее простое утверждение показывает, что понятие следования (выводимости) можно переформулировать в терминах тождественной истинности (см. определение 3.4).

Предложение 6.1. H-формула является следствием множества H-формул F тогда и только тогда, когда формула

(*)

является истинной на всех наборах значений переменных (т.е. тождественно истинной).

Доказательство непосредственно следует из определения значений конъюнкции и импликации.

Как уже отмечалось в п.3, проблема проверки по булевой формуле ее тождественной истинности является весьма сложной. Известный нам метод такой проверки с помощью построения таблицы значений на всех наборах переменных практически не работает уже для формул с несколькими десятками переменных. В то же время во многих практических задачах число логических параметров исчисляется сотнями. Оказывается, что для установления тождественной истинности формул вида (*) или, что то же самое, для задачи проверки условия для H-формул имеется простой и очень эффективный алгоритм, позволяющий ее решать для формул с сотнями и тысячами переменных.

Мы изложим этот алгоритм на примере одного из интересных "экономических" приложений H-формул - задачи о возможности производства заданной продукции (набора товаров) из некоторого множества исходных продуктов (товаров, сырья).