Совершенные днф и кнф

Рассмотрим произвольную булеву функцию f(X₁,…,X_n) , зависящую от переменных из . Oбозначим через N_f⁺ множество наборов значений переменных, на которых f принимает значение 1, а через N_f^- множество наборов, на которых f принимает значение 0, т.е. и

Определим по этим множествам две формулы:

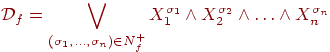
и

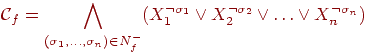
Теорема 4.1.

1. Если функция f не равна тождественно 0, то формула 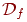- это совершенная ДНФ, задающая функцию f.

2. Если функция f не равна тождественно 1, то формула 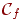- это совершенная КНФ, задающая функцию f.

Доказательство получается непосредственным вычислением значения каждой из указанных формул с учетом того, что для любого σ {0, 1} имеют место равенства: 1^σ = σ и 0^σ = ¬σ (см. задачу 4.4).

Следствие 4.1.1. Каждая булева функция может быть задана формулой, содержащей переменные и функции конъюнкции, дизъюнкции и отрицания.

Приведенные выше формулы для и позволяют эффективно строить совершенные ДНФ и КН по табличному представлению функции f (Каким образом?). Можно ли получить такие специальные представления по произвольной формуле, задающей f, не выписывая ее полной таблицы? Приводимая ниже процедура позволяет это сделать, используя основные эквивалентности формул.

Процедура Приведение к совершенной ДНФ

Вход: формула Φ, включающая функции ¬, , , и +.

1. Используя эквивалентность (7), заменить все вхождения функции в Φ на ¬, и , затем использовать эквивалентность (8) для замены всех вхождений функции + на ¬, и .

2. Используя законы де Моргана (5) и снятия двойного отрицания(4), внести все знаки отрицания внутрь скобок так, чтобы все оставшиеся отрицания находились непосредственно перед переменными.

3. Получившаяся после шага (2) формула имеет одну из двух форм:

   • или

   • .

Поскольку каждая из формул Φ₁ , Φ₂ имеет меньшую глубину, чем формула Φ', то предположим по индукции, что для них уже построены эквивалентные ДНФ и , соответственно.

Тогда в случае (а) имеем:

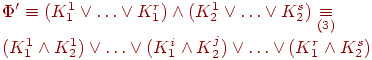
Каждый член этой дизъюнкции представляет собой конъюнкцию переменных и их отрицаний. Применяя эквивалентности групп (1), (2) и (6), можно удалить из нее повторения переменных, после чего она превратится в некоторую элементарную конъюнкцию или константу. Проделав такие преобразования со всеми парами (i,j), 1 i r, 1 j s, и удалив, если потребуется, константы 0, мы получим ДНФ, эквивалентную исходной формуле Φ.

В случае (б) формула сама уже является ДНФ.

4. Используя эквивалентности групп (1), (2) и (6), удалить из получившейся после шага (3) формулы повторные вхождения одинаковых конъюнкций.

5. Пусть после шага (4) получилась ДНФ 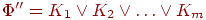. Чтобы получить эквивалентную совершенную ДНФ, построим для каждой K_i (i=1,…, m) , эквивалентную совершенную ДНФ (см. задачу 4.5),заменим ею K_i , а затем устраним повторения одинаковых конъюнкций.

Из формулировок эквивалентностей (7) и (8) непосредственно вытекает

Предложение 4.1. На этапе (1) процедуры при последовательном выполнении преобразований (7), а затем - (8), до тех пор, пока ни одно из них не применимо, полученная в результате формула не будет содержать функций и +.

Доказательство этого предложения оставляем в виде упражнения (см. задачу 4.7).

Следующее утверждение гарантирует корректность этапа (2).

Предложение 4.2. На этапе (2) процедуры при любом порядке выполнения преобразований групп (4) и (5) до тех пор, пока ни одно из них не применимо, в полученной в результате формуле все знаки отрицания будут стоять непосредственно перед переменными.

Перед доказательством этого утверждения введем некоторые обозначения. Напомним, что в определениях 3.2 и 3.3 для каждой формулы Φ была определена ее глубина dep(Φ). Например, формула Φ=¬(X+Y) (¬(X ¬ Z) Y), построенная над системой F={ , , ¬, , +}, имеет глубину dep(Φ)=5.

Пусть Φ - это формула над F={ , , ¬}. Определим для каждой ее "отрицательной" подформулы вида ¬(Ψ) высоту h(¬(Ψ)) как 3^dep(Ψ)-1 . И пусть высота всей формулы H(Φ) равна сумме высот всех ее отрицательных подформул. Например, для приведенной выше формулы Φ ее высота равна H(Φ)= h(¬(X+Y)) +h(¬(X ¬ Z))+ h(¬ Z) = (3¹-1) + (3²-1) +(3⁰-1) = 10.

Доказательство предложения 4.2 проведем индукцией по высоте формул.

Базис индукции. Если H(Φ)=0, то либо в Φ нет отрицаний, либо все отрицания находятся непосредственно перед переменными. Следовательно, Φ удовлетворяет требованию предложения 4.2.

Шаг индукции. Предположим, что при n k для всех формул высоты n Предложение 4.2 выполнено. Пусть Φ - произвольная формула высоты H(Φ)= k+1. Докажем наше утверждение для нее. Поскольку H(Φ) 1, то Φ содержит хотя бы одну отрицательную подформулу ¬(Ψ), у которой h(¬(Ψ)) 1 и, следовательно, dep(Ψ) 1. К такой формуле обязательно можно применить либо снятие двойного отрицания (4), либо один из законов де Моргана (5). (Объясните почему.) Пусть ¬(Ψ) - это та подформула Φ, которая на (2)-ом этапе процедуры первой заменяется на эквивалентную формулу Ψ' в соответствии с одной из указанных эквивалентностей. Пусть Φ' - это формула, получившаяся в результате этой замены из Φ. Нетрудно проверить (проделайте эту проверку!), что при любом из преобразований (4), (5) H(Ψ') < H(¬(Ψ)) и, следовательно, H(Φ') < H(Φ). Тогда H(Φ') k и по предположению индукции применение эквивалентностей (4), (5) в произвольном порядке приведет в конце концов к формуле, у которой все отрицания будут стоять непосредственно перед переменными. Тем самым, предложение 4.2 выполнено при n=k+1, что завершает индукционный шаг и все доказательство.

Рассмотрим применение процедуры приведения к совершенной ДНФ на примере.

Пример 4.1. Пусть формула .

На (1)-ом этапе процедуры получаем следующую цепочку эквивалентностей:

На (2)-ом этапе вносим отрицание внутрь первой скобки и получаем формулу

Устранив двойное отрицание, получим

Нетрудно видеть, что это уже ДНФ. Удалим на (4)-ом этапе повторное вхождение первой конънкции и получим ДНФ

Эта ДНФ не является совершенной, так как в каждую из ее трех конъюнкций входят не все переменные. Построим на этапе (5) для них эквивалентные совершенные ДНФ (используя решение задачи 4.5).

Подставив эти формулы в Φ₁ и устранив повторения конъюнкций, получим совершенную ДНФ, эквивалентную исходной формуле Φ:

Мы видим, что ДНФ Φ₁ , полученная после 4-го этапа, выглядит существенно проще, т.е. является более короткой, чем совершенная ДНФ Φ₂ . Однако совершенные ДНФ и КНФ обладают важным свойством единственности, которое следует из их конструкции в теореме 4.1.

Следствие 4.1.2. Для каждой булевой функции от n переменных, не равной тождественно 0, существует единственная с точностью до перестановки конъюнкций и переменных внутри конъюнкций совершенная ДНФ, задающая эту функцию.

Это следствие позволяет предложить следующую процедуру для проверки эквивалентности формул Φ и Ψ.

1. Построить для Φ и Ψ эквивалентные совершенные ДНФ Φ' и Ψ' используя процедуру приведения к совершенной ДНФ.

2. Упорядочить в соответствии с нумерацией переменных X вхождения переменных в каждую конъюнкцию, а затем лексикографически упорядочить между собой конъюнкции, входящие в Φ' и Ψ'. Пусть в результате получатся совершенные ДНФ Φ'' и Ψ''

3. Если Φ'' = Ψ'', то выдать ответ "Да", иначе - ответ "Нет".

Замечание. Аналогичную процедуру можно построить с использованием совершенных КНФ.