Розрахунково-графічна робота

“Дослідження геометричних характеристик перерізів та розрахунок балок на міцність”

Зміст роботи

Задача №1

Дослідження геометричних характеристик складного перерізу

Для заданого плоского поперечного перерізу, що складається з декількох елементів, визначити основні геометричні характеристики.

При дослідженні геометричних характеристик складного перерізу потрібно:

1. Визначити положення центру перерізу відносно допоміжних осей.

2. Обчислити осьові моменти інерції відносно головних центральних осей.

3. Визначити моменти опору перерізу при згині та радіуси інерції.

Задача №2

Розрахунок на міцність однопрольотної сталевої двотаврової балки на шарнірних опорах

Для однопрольотної сталевої шарнірно обіпертої балки побудувати епюри Q і M аналітичним методом та визначити з умови міцності за нормальними напруженнями номер стандартного прокатного двотаврового профілю при [ ϭ ] = 160 МПа.

При розв’язуванні задачі потрібно:

1. Визначити реакції опор аналітичним методом і виконати перевірку визначення реакцій.

2. Скласти рівняння реакцій поперечних сил Q(z) і згинальних моментів M(z) для кожної ділянки балки та побудувати відповідні епюри.

3. Підібрати номер двотаврового профілю, який забезпечує міцність балки.

Задача №3

Розрахунок на міцність дерев’яної консольної балки

Для консольної клеєної дерев’яної балки прямокутного перерізу із заданим співвідношенням ^h/_b побудувати епюри Q і M, визначити розміри перерізу з умови міцності за нормальними напруженнями при [ ϭ ] = 14 МПа та виконати перевірку міцності за дотичними напруженнями при [ τ ] = 2 МПа.

При розв’язуванні задачі потрібно:

1. Скласти рівняння Q(z) і M(z) для кожної ділянки балки і побудувати епюри.

2. Підібрати розміри прямокутного перерізу при заданому співвідношенні ^h/_b.

3. Виконати перевірку міцності за дотичними напруженнями.

Задача №1

Дослідження геометричних характеристик складного перерізу

Хід виконання задачі №1 показаний на прикладі визначення геометричних характеристик перерізу, що складається з трьох елементів: швелера №16 і двотавра №20,20.

1. Заданий складний переріз викреслюється на форматі А4 в певному масштабі (ДСТУ ISO 128-50:2005). На креслення наносяться центральні осі кожного з складових елементів – швелера, двотавра, відповідно x₁y₁, x₂y₂, x₃y₃ з центрами c₁, c₂, c₃.

2. Проводиться допоміжна вісь Y₀ паралельно осям Y₁, Y₂, і Y₃ для визначення положення центра складного перерізу і центральної осі Y. Другу допоміжну вісь обирати непотрібно, тому що положення центральної осі y відомо – це вісь симетрії перерізу.

3. З таблиць сортаментів прокатної сталі виписуються необхідні дані для швелера і двотавра.

I – прямокутник 180х10	II – швелер №14	III – двотавр №16
h1 = 16см	h2 = 14см	h3 = 16см
b1 = 6,4см	b2 = 5,8см	b3 = 8,1см
A1 = 18,1см2	d2= 0,49см	A3 = 20,2см2
= = 63,6см4	A2 = 16,6см2	= = 58,6см4
= 1,8см	= 49,1см4	= = 873см4
= = 747см4	= 45,4см4	d3 = 0,5см
	Z2=1,62 см

4. Визначаються координати центрів c₁, c₂ і c₃ складових елементів перерізу вілносно допоміжної осі X₀.

Y₁ = 0,5 * b₁ = 0,5 * 1 = 0,5см

Y₂ = b₁ + b₂ – z_{0 2}= 1+ 5,8 – 1,62 = 5,18см

Y₃ = b₁ + b₂ + 0,5 * h₃ = 1 + 5,8 + 0,5 * 16 = 14,8см

5. Обчислюється координата центру складного перерізу:

Y_c = = = 7,18см

6. Проводиться центральна вісь X через центр С складного перерізу паралельно допоміжній осі X₀.

7. Визначаються величини осьових моментів інерції складного перерізу.

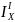= + * A₁ =486+(-6,68)² *18=1289,2см⁴

α₁ = Х₁ – Х₀ = 0,5 – 7,18 = - 6,68см

= + * A₁ = 1,5 + 1² * 18 = 19,5см⁴

b₁ = 1 см

= + * A₂ = 491 + (-2)² *16,6 = 557,4см⁴

a₂ = x₂ – x₀ = 5,18 – 7,18 = -2 см

= + * A₂ = 45,4 + 5,8² * 16,6 = 603,8см⁴

b₂ = 5,8 см

= + * A₃ =5,86 + 7,62² * 20,2 = 1231,5см⁴

a₃ = X₃ – X₀ = 14,8 – 7,18 = 7,62см

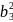= + * A₃ = 873 + 8,1 * 20,2 = 2198,3см⁴

b₃ = 8,1

I_X = + + = 1289,2 + 557,4 + 1231,5 = 3078,1см⁴

I_Y = + + = 19,5 + 603,8 + 2198,3 = 2821,6см⁴

8. Визначаємо величини моментів опору перерізів.

W_x = = = 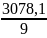342см³

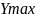= Y_c = 18,13см

W_y = = = 180,6см³

X_max = h₂ = 10см

9. Визначаються величини головних радіусів інерції перерізу:

τ_x = = = = 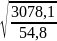7,49см

τ_y = = = = 7,17см

Задача №2

Розрахунок на міцність однопрольотної сталевої двотаврової балки на шарнірних опорах

1. Для заданої схеми балки визначаються реакції опор.

Складаються рівняння рівноваги:

∑ M_A = 0; - q * 10 * 5 + M – F * 7 + R_B * 10 = 0

R_B * 10 = 250 – 70 + 7 = 0

R_B = = 25кН

∑ M_B= 0; F - 3 + M + q * 10 * 5 – R_A * 10 = 0

– R_A * 10 = - 30 + 70 * 250 = 0

R_A = = 35кН

Перевірка ∑_Y = 0

R_A – F – q * 10 + R_B = 25 – 10 – 50 + 35 = 0

2. Складаються рівняння Q(z) і M(z).

Ділянка 1

0 ≤ z₁ ≤ 5

Q(z₁) = R_A – q*z₁

Q(0) = 36кН

Q(5) = 35-5*5=10кН

M(z₁) = R_A * z₁ – q*z₁*

M(0) = 35 * 0 – 5*0 = 0 кН/м

M(5) = 35 * 5*5 = 112,5 кН/м

Ділянка 2

5 ≤ z₂ ≤ 7

Q(z₂) = R_A – q * Z₂

Q(5) = 35 – 5 * 5 =10 кН

Q(7) = 35 - 5 * 7 = 0 кН

M(z₂) = R_A * Z₂ – M – q* Z₂

M(5) = 35 * 5 – 70 – 5 * 5 = 42,5 кН/м

M(7) = 35 * 7 – 70 – 5 * 7 = 52,5 кН/м

Ділянка 3

0 ≤ z₃ ≤ 3

Q(z₃) = - R_B +q * z₃

Q(0) = - 25 + 5 * 0 = - 25 кН

Q(3) = - 25+5 * 3 = - 10 кН

M(z₃) = R_B * z₃ – q * z₃ *

M(0) = 25 * 0 = 0 кН/м

M(3) = 25 * 3-5*3 = 52,5 кН/м

За даними підрахунків будуються епюри Q(z) і M(z).

3. Підбирається необхідний номер двотавра з умови міцності. Небезпечним є переріз, де виникає найбільший за величиною момент M_max = 160кН/м.

ϭ_max = = [ ϭ ]

W_x = = = 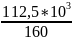765,6см³

За таблицями сортаменту обираэмо двотавр:

№ 36; W_x = 743см³

№ 40; W_x = 953см³

Визначаємо нормальні напруження для двотавра № 36:

ϭ_max = = = 151,4МПа < [ ϭ ] = 160МПа

Міцність балки забезпечена.

Задача №3

Розрахунок на міцність дерев’яної консольної балки

1. Складаємо рівняння Q(z) і M(z). При цьому початок координат обирається у вільному кінці консолі, що позбавляє від необхідності визначення реакцій опори.

Переріз (1-1)

0 ≤ z₁ ≤ 2

Q(z₁) = F

Q(0) =10кН

Q(2) = 10кН

M(z₁) = F * z₁

M(0) = 10 * 0 = 0кН/м

M(2) = 10 * 2 = 20кН/м

Переріз (2-2)

2 ≤ z₂ ≤ 6

Q(z₂) = F – q *(z₂ – 2)

Q(2) = 10 - 4 * (2 - 2) = 10 кН

Q(6) = 10 - 4 * (6 – 2) = - 6кН

M(z₂) = F * z₂ – q * (z₂ - 2)* - M

M(2) = 10 * 2 – 4 * (2 - 2)* - 25 = - 5кН/м

M(6) = F * 6 – 4 * (6 - 2)* - 25 = 3кН/м

M(4,5) = 10 * 4,5 – 4 * (4,5 - 2)* - 25 = 3кН/м

F - q * (Z₀ - 2)

10 =4 * (Z₀ - 2)

Z₀ – 2 = 10/4 = 2,5

Z₀ = 2 + 2,5 = 4,5

Переріз (3-3)

6 ≤ z₃ ≤ 8

Q(z₃) = F – q *4

Q(6) = 10 - 4 * 4 = - 6кН

Q(8) = 10 - 4 * 4 = - 6кН

M(z₃) = F * z₃ – M * q * 4 * (z₃ - 4 )

M(7) = 10 * 6 – 25 * 4 * 4 * (6 - 4 ) = 3кН/м

M(8) = F * 8 – 25 * 4 * 4 * (8 - 4 ) = - 9кН/м

2. Підбирається необхідний з умови міцності прямокутний переріз. Небезпечним є переріз, де виникає найбільший за величиною згинальний момент M_max = 12кН/м.

W_x = = 1333,3см³

Визначаємо геометричні розміри прямокутного дерев’яного перерізу балки.

W_x = = =

при = 1,2 => b =

= 1333,3

h³ = 7,2 * 1333,3

h = 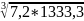= (9599,8)^0,3333333 = 21,3см

Приймаємо h = 21см

b = = = 17,8см

Приймаємо b = 18см

Визначаємо дійсний момент опору:

W_x = = 1323см³

Перевіряється виконання умови міцності:

ϭ_max = = 15,1МПа > [ ϭ ] = 15МПа

∆δ = * 100 = * 100 = 0,6 % <[ 5 %]

Міцність балки за нормальними напруженнями забезпечена.

Отже приймаємо остаточно:

h = 21см, b = 18см

3. Перевірка на міцність за дотичними напруженнями. Небезпечним є переріз, де виникає найбільша за величиною поперечна сила Q_max = 10кН.

τ_max = * 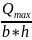= * = 0,48МПа ≤ [ τ ] = 2МПа

Міцність за дотичними напруженнями забезпечена.