13. Законы Фика для диффузии примесных атомов

Процесс диффузии заключается в самопроизвольном стремлении системы к выравниванию концентраций атомов. Атомы А перемещаются в том направлении, где их меньше. Перенос атомов в системе происходит в результате хаотических блужданий. Таким образом, в системе одновременно сосущест- вуют два вида движения частиц: хаотическое—тепловое и на- правленное—дрейф. Второе обязано некй движущей силе, действующей в системе. Такой силой может быть градиент: кон- центрации, температуры, электрического поля или в общем случае — химического потенциала. Макроскопическая теория диффузии рассматривает основ- ную задачу: проникновение растворяемого вещества с по- верхности твердого тела (растворителя) в его объем. Соот- ветственно решением этой задачи является распределение концентрации С (х, у, z, t, T), т.е. зависимость концент- рации диффундирующих частиц С от координат х, у, z, времени процесса t и температуры Т при поверхностной начальной концентрации С₀. Модификацией этой задачи является другая: установить характер перераспределения начального распределения частиц в объеме С₀(х, у, z) при действии одной или несколь ких движущих сил.При этом очевидны два обстоятельства. Первое состоит в том, что макротеория отвлекается от механизма диффузии, т.е. не анализирует способ перемещения атомов диффузанта в твердом теле. Отсюда: природа вещества, в котором протекает диффузия, будет присутствовать в макроскопических решениях в виде неких параметров, определяющих процесс. Для упрощения сделаем еще предположение о диффузии только в одном на- правлении х и независимости концентрации С от других координат у, z. Тогда количество вещества dq, диффундирующего за время dt через поверхность S, будет dq = —DS (дС/дх) dt, где dC/dx — градиент концентрации — движущая сила; D — параметр процесса, называемый коэффициентом диффузии. Он зависит от природы диффузанта и растворителя. Введем понятие плотности диффузионного потока j =

dq/Sdτ как количество диффундирующего вещества dq че- рез единицу поверхности тела в единицу времени. Для изо- тропной среды в одномерном случае получим j = -D (дС/дх). Это выражение носит название первого закона Фика} Знак минус в этом выражении показывает, что поток направлен из области с большей концентрацией в область с меньшей концентрацией. Изменение концентрации диффузанта во времени и в про- странстве описывает второй закон Фика:

Второй закон Фика представляет собой уравнение в частных производных, и для его решения необходимо задать на- чальные и граничные условия. Начальное условие С (х, у, z, t) при t = 0 чаще всего принимается либо равным нулю, либо постоянной С₀. При задании граничных условий, т.е. условий на поверх- ности, обычно задают концентрацию С (0, t) или поток (dC/dx). В результате решения уравнения (2закон) получают рас- пределение концентрации по толщине образца во времени С (х, t) или для трехмерного случая: С (х, у, z, t). В решениях этих уравнений ве- личина имеет

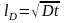размерность длины и характеризует расстояние, на котором концентрация диффундирующих атомов спадает в е раз. Этот путь называют диффузионной длиной.

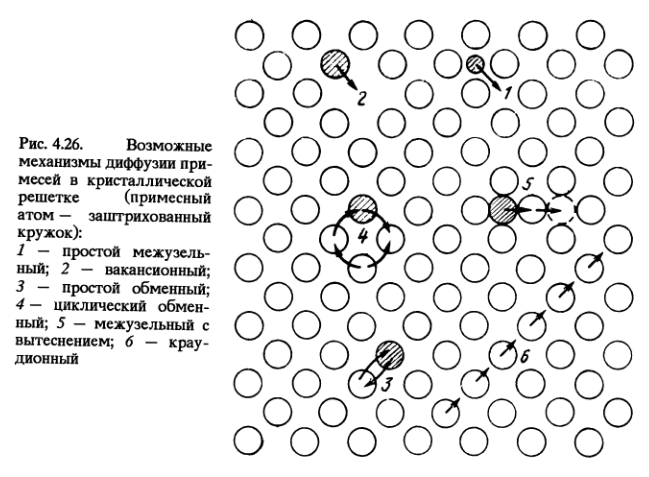
При диффузии по механизму вытеснения (5) атом сначала попадает в межузлие, а затем выталкивает ближайший сосед- ний атом из узла и становится на его место. Вытесненный в межузлие атом выталкивает следующего соседа и т.д. Под номером 6 на рис. 4.26 показан краудионный механизм1. Краудион представляет группу атомов, сжатую из-за присут-

ствия в их ряду лишнего атома. Диффузия происходит путем небольших смещений каждого атома этого ряда вдоль некото- рого направления. Диффузионный перескок атома, соседнего с вакансией, происходит следующим образом. €Атом ν раз в секунду ударяется о барьер из атомов, окружающих вакантный узел. …Если его энергия в какой-то момент времени будет достаточна для того, чтобы преодолеть этот барьер (рис. 1), то атом занимает вакантный узел V, перемещаясь в соседнюю кристаллографическую ячейку. При этом вакансия перемещается как бы ему навстречу (см. рис. 1).