§ 6. Метод вариации произвольных постоянных.
Применим
этот метод для решения ЛНС ДУ (5.1). Общее
решение ЛОС ДУ (3.1) дается формулой
где
и
- произвольные постоянные. Будем искать
решение системы (5.1) в виде
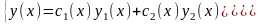(6.1)
где
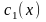и
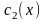- функции, подлежащие определению.
Подставим
(6.1) в (5.1):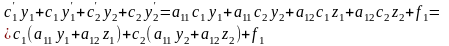
Откуда
получаем
Аналогично
получаем второе уравнение для функций
:
.
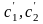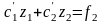Итак,
для производных
имеем систему уравнений
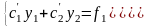(6.2)
определитель
которой есть определитель Вронского
для фундаментальной системы решений
системы (3.1), который не обращается в
нуль ни в одной точке (a,b).
Поэтому решая систему (6.2), однозначно
определяются
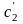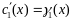и
:
и
.
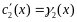Интегрируем эти выражения и подставляем
результат в формулу (6.1).
34. Структура общего решения линейной неоднородной системы. Формула Коши.
При
помощи формулы Коши можно выразить
решение линейной неоднородной системы
дифференциальных уравнений через
некоторую фундаментальную систему
решений соответствующей однородной
линейной системы.
Рассмотрим
неоднородную линейную систему
дифференциальных уравнений (2),
записанную в векторном виде
Соответствующая
ей однородная система (3)
Пусть
–
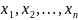фундаментальная система решения системы
уравнений (3). Образуем матрицу
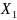(t),
столбцы которой являются этими
решениями:
Определитель
матрицы
(t)
представляет собой определитель
Вронского. Он отличен от нуля для всех
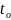[a,
b]. Следовательно, существует обратная
матрица
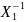(t)
при каждом
[а,
b]. Составим матрицу
X(t,
)
=
(t)
(
)
Столбцы этой матрицы также образуют
фундаментальную систему решений системы
уравнений (3). Отметим, что X(t,
)=
Назовем
матрицу X(t,
)
фундаментальной матрицей системы (3).
Эта матрица удовлетворяет матричному
уравнению
Решение x(t) системы уравнений (3), удовлетворяющее начальным условиям x( )= , можно записать в виде
Тогда можно показать, что следующая формула, называемая формулой Коши, позволяет найти решение x(t) неоднородной системы (2), удовлетворяющее начальным условиям x( )= , если известна фундаментальная матрица X(t, ) однородной системы (3):
Следует отметить, что если матрица А постоянная, т. е. рассматриваемая система дифференциальных уравнений является системой линейных уравнений с постоянными коэффициентами
то решение этой системы x(t), удовлетворяющее начальным условиям x( )= , запишется в виде
где X (f) — матрица, столбцы которой состоят из фундаментальной системы решений однородной системы уравнений xt'=Ах, причем X ( ) = E.